Antenna Placement
Time Limit:1000MS? Memory Limit:65536K
Total Submit:380 Accepted:125
Description
The Global Aerial Research Centre has been allotted the task of building the fifth generation of mobile phone nets in Sweden. The most striking reason why they got the job, is their discovery of a new, highly noise resistant, antenna. It is called 4DAir, and comes in four types. Each type can only transmit and receive signals in a direction aligned with a (slightly skewed) latitudinal and longitudinal grid, because of the interacting electromagnetic field of the earth. The four types correspond to antennas operating in the directions north, west, south, and east, respectively. Below is an example picture of places of interest, depicted by twelve small rings, and nine 4DAir antennas depicted by ellipses covering them.
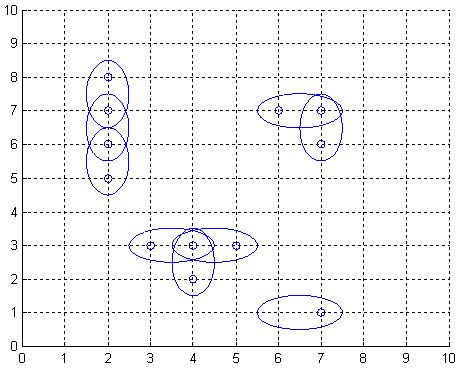
Obviously, it is desirable to use as few antennas as possible, but still provide coverage for each place of interest. We model the problem as follows: Let A be a rectangular matrix describing the surface of Sweden, where an entry of A either is a point of interest, which must be covered by at least one antenna, or empty space. Antennas can only be positioned at an entry in A. When an antenna is placed at row r and column c, this entry is considered covered, but also one of the neighbouring entries (c+1,r),(c,r+1),(c-1,r), or (c,r-1), is covered depending on the type chosen for this particular antenna. What is the least number of antennas for which there exists a placement in A such that all points of interest are covered?
Input
On the first row of input is a single positive integer n, specifying the number of scenarios that follow. Each scenario begins with a row containing two positive integers h and w, with 1 <= h <= 40 and 0 < w <= 10. Thereafter is a matrix presented, describing the points of interest in Sweden in the form of h lines, each containing w characters from the set ['*','o']. A '*'-character symbolises a point of interest, whereas a 'o'-character represents open space.
Output
For each scenario, output the minimum number of antennas necessary to cover all '*'-entries in the scenario's matrix, on a row of its own.
Sample Input
2
7 9
ooo**oooo
**oo*ooo*
o*oo**o**
ooooooooo
*******oo
o*o*oo*oo
*******oo
10 1
*
*
*
o
*
*
*
*
*
*
Sample Output
17
5
Source
Svenskt M?sterskap i Programmering/Norgesmesterskapet 2001
myCode:
#include?
<
iostream
>
using
?
namespace
?std;
const
?
int
?INF?
=
?
1
?
<<
?
28
;
int
?n,?r,?c;
int
?e[
11
]?
=
?
{
1
,?
2
,?
4
,?
8
,?
16
,?
32
,?
64
,?
128
,?
256
,?
512
,?
1024
}
;
char
?m[
50
][
20
];
int
?d[
50
][
1024
];
int
?b[
20
];
int
?cc[
20
];
int
?ss;
void
?Try(
int
?x,?
int
?s)
{
????
if
?(x?
>=
?c)?
{
????????
int
?k?
=
?
0
;
????????
for
?(
int
?i
=
0
;?i
<
c;?i
++
)?
{
????????????k?
+=
?b[i]?
*
?e[i];
????????}
????????
if
?(d[
0
][k]?
==
?
-
1
?
||
?d[
0
][k]?
>
?s)
????????????d[
0
][k]?
=
?s;
????????
return
?;
????}
????
if
?(m[
0
][x]?
==
?
'
o
'
)?
{
????????Try(x
+
1
,?s);
????}
?
else
?
if
?(m[
0
][x]?
==
?
'
*
'
)?
{
????????
int
?t1?
=
?b[x],?t2?
=
?b[x
+
1
],?t3?
=
?s;
????????b[x]?
=
?
1
;?b[x
+
1
]?
=
?
1
;?s?
+=
?
1
;
????????Try(x
+
2
,?s);
????????b[x]?
=
?t1;?b[x
+
1
]?
=
?t2;?s?
=
?t3;
????????
if
?(r?
!=
?
1
?
||
?m[
0
][x]?
==
?
'
o
'
)?Try(x
+
1
,?s);
????}
??
}
void
?DFS(
int
?i,?
int
?x,?
int
?s)
{
????
if
?(x?
>=
?c)?
{
????????
int
?k?
=
?
0
;
????????
for
?(
int
?j
=
0
;?j
<
c;?j
++
)?
{
????????????k?
+=
?cc[j]?
*
?e[j];
????????}
????????
if
?(d[i][k]?
==
?
-
1
?
||
?d[i][k]?
>
?ss?
+
?s)
????????????d[i][k]?
=
?ss?
+
?s;
????????
return
?;
????}
????
if
?(b[x]?
==
?
0
)?
{
????????
if
?(m[i
-
1
][x]?
==
?
'
*
'
)?
{
????????????cc[x]?
=
?
1
;?s?
+=
?
1
;
????????????DFS(i,?x
+
1
,?s);
????????}
?
else
?
{
????????????
if
?(m[i][x]?
==
?
'
*
'
)?
{
????????????????
int
?t1?
=
?cc[x],?t2?
=
?cc[x
+
1
],?t3?
=
?s;
????????????????cc[x]?
=
?
1
;??cc[x
+
1
]?
=
?
1
;?s?
+=
?
1
;
????????????????
if
?(b[x
+
1
]?
==
?
0
?
&&
?m[i
-
1
][x
+
1
]?
==
?
'
*
'
)
????????????????????s?
+=
?
1
;
????????????????DFS(i,?x
+
2
,?s);
????????????????cc[x]?
=
?t1;?cc[x
+
1
]?
=
?t2;?s?
=
?t3;
????????????????
if
?(i?
!=
?r
-
1
?
||
?m[i][x]?
==
?
'
o
'
)?DFS(i,?x
+
1
,?s);
????????????}
?
else
?
if
?(m[i][x]?
==
?
'
o
'
)?
{
????????????????DFS(i,?x
+
1
,?s);
????????????}
????????}
????}
?
else
?
{
????????????
if
?(m[i][x]?
==
?
'
*
'
)?
{
????????????????
int
?t1?
=
?cc[x],?t2?
=
?cc[x
+
1
],?t3?
=
?s;
????????????????cc[x]?
=
?
1
;??cc[x
+
1
]?
=
?
1
;?s?
+=
?
1
;
????????????????
if
?(b[x
+
1
]?
==
?
0
?
&&
?m[i
-
1
][x
+
1
]?
==
?
'
*
'
)
????????????????????s?
+=
?
1
;
????????????????DFS(i,?x
+
2
,?s);
????????????????cc[x]?
=
?t1;?cc[x
+
1
]?
=
?t2;?s?
=
?t3;
????????????????
if
?(i?
!=
?r
-
1
?
||
?m[i][x]?
==
?
'
o
'
)?DFS(i,?x
+
1
,?s);
????????????}
?
else
?
if
?(m[i][x]?
==
?
'
o
'
)?
{
????????????????DFS(i,?x
+
1
,?s);
????????????}
??????
????}
}
void
?init()
{
????memset(d[
0
],?
-
1
,?
sizeof
(d[
0
]));
????memset(b,?
0
,?
sizeof
(b));
????Try(
0
,?
0
);
}
void
?Solve()?
{
????
int
?i,?j,?k;
????init();
????
for
?(i
=
0
;?i
<
r
-
1
;?i
++
)?
{
????????memset(d[i
+
1
],?
-
1
,?
sizeof
(d[i
+
1
]));
????????
for
?(k
=
0
;?k
<
e[c];?k
++
)?
{
????????????
if
?(d[i][k]?
!=
?
-
1
)?
{
????????????????
int
?t?
=
?k,?j?
=
?
0
,?kk?
=
?
0
;
????????????????memset(b,?
0
,?
sizeof
(b));
????????????????memset(cc,?
0
,?
sizeof
(cc));
????????????????
while
?(t?
!=
?
0
)?
{
????????????????????b[j
++
]?
=
?t?
%
?
2
;
????????????????????t?
/=
?
2
;
????????????????}
????????????????ss?
=
?d[i][k];
????????????????DFS(i
+
1
,?
0
,?
0
);
????????????}
????????}
????}
????
int
?ans?
=
?INF;
????
for
?(k
=
0
;?k
<
e[c];?k
++
)?
{
????????
if
?(d[r
-
1
][k]?
!=
?
-
1
?
&&
?d[r
-
1
][k]?
<
?ans)?
{
????????????ans?
=
?d[r
-
1
][k];
????????}
????}
????cout?
<<
?ans?
<<
?endl;
}
int
?main()
{?
????cin?
>>
?n;
????
while
?(n
--
?
!=
?
0
)?
{
????????cin?
>>
?r?
>>
?c;
????????
for
?(
int
?i
=
0
;?i
<
r;?i
++
)?cin?
>>
?m[i];
????????Solve();
????}
????system(
"
pause
"
);
????
return
?
0
;
}
ghost_wei大牛的code,? 放出來供大家學習,? 用了滾動數組優化, 而且位運算用得出神入化:)
#include<iostream.h>
#include?<fstream.h>
const?int?k2[11]={1,2,4,8,16,32,64,128,256,512,1024};
int?n,m,c[2][1024];
char?d[40][10];
inline?void?min(int?&i,int?j)
{
????if?(i>j)?i=j;
}
void?work()
{
????int?i,j,km,k,e7,e8,l,t,ans;
????km=k2[m];
????for?(i=0;i<km;i++)?c[0][i]=100000;
????c[0][0]=0;
????e7=0;?e8=1;
????for?(i=0;i<n;i++)
????{
????????for?(j=0;j<km;j++)?c[e8][j]=100000;
????????for?(j=1;j<m;j++)
????????????if?(d[i][j]=='*')
????????????????for?(k=0;k<km;k++)
????????????????????min(c[e7][k|k2[j]|k2[j-1]],c[e7][k]+1);
????????for?(k=0;k<km;k++)
????????{
????????????l=0;?t=0;
????????????for?(j=0;j<m;j++)?
????????????????if?(!(k&k2[j])&&d[i][j]=='*')
????????????????{
????????????????????l+=k2[j];
????????????????????t++;
????????????????}
????????????min(c[e8][l],c[e7][k]+t);
????????}
????????e7=e7^1;?e8=e8^1;
????}
????ans=100000;
????for?(k=0;k<km;k++)
????????min(ans,c[e7][k]);
????cout<<ans<<endl;
}
int?main()
{
????int?tc,cas,i,j;
????cin>>tc;
????for?(cas=1;cas<=tc;cas++)
????{
????????cin>>n>>m;
????????for?(i=0;i<n;i++)
????????????for(j=0;j<m;j++)
????????????????cin>>d[i][j];
????????work();
????}
????return?0;
}
posted on 2006-10-18 17:29
豪 閱讀(2137)
評論(4) 編輯 收藏 引用 所屬分類:
ACM題目