A. Period PKU 1961 http://poj.org/problem?id=1961
題意：給定一個長度為N(N <= 106)的字符串S，求它的所有前綴中能夠表示成AK的前綴，并且要求求出每個前綴對應(yīng)的K。
題解：KMP
利用KMP求出該串的Next數(shù)組，然后枚舉每個前綴，根據(jù)Next數(shù)組的定義，對于某個前綴S[1...i]，有S[1...Next[i]] = S[i-Next[i]+1...i]，假設(shè)前綴S[1...i]能夠表示長AK的形式，則A = S[Next[i]+1...i]，所以必須滿足i能夠被i - Next[i] 整除，滿足條件后K = i/( i - Next[i])。
B. Corporative Network
PKU 1962 http://poj.org/problem?id=1962
題意：給定N(N <= 20000)個點和M(M <= 200000)次操作，每次操作有兩種類型：
I a b 將a的父結(jié)點設(shè)為b，并且合并距離為 |a-b| mod 1000
E a 詢問a到根結(jié)點的合并距離。
題解：并查集
利用路徑壓縮的思想，用dist[p]表示p和p的父結(jié)點的合并距離，每次查詢的時候累加p到根結(jié)點的合并距離，并且將p到p所在樹的根結(jié)點R的路徑上的所有點的父結(jié)點都設(shè)為R，然后更新各自的合并距離。
合并操作O(1)，查詢操作總復(fù)雜度O(N)。
C. Cave Exploration
PKU 1963 http://poj.org/problem?id=1963
題意：給出N(N <= 1000)條水平或者垂直的走廊，再給定走廊上任意一個坐標(biāo)點作為起點以及方向，按照以下策略走：能夠左轉(zhuǎn)就左轉(zhuǎn)，不能則筆直走，不能筆直走就右轉(zhuǎn)，都不能就掉頭。這樣走最后繞一圈又會回到起點，問哪些走廊是沒有經(jīng)過的，只要有一個點走過就算經(jīng)過。
題解：模擬 + 哈希。
將水平線段和豎直線段分開存，分兩種情況討論：
1、水平線段
對于任意一根水平線段，枚舉所有的豎直線段，計算出交點和水平線段的端點，保存下來并且按x坐標(biāo)遞增排序，去掉重復(fù)點，利用雙向鏈表將兩個相鄰點連接起來，由于x和y坐標(biāo)范圍為-32767~32767，而交點數(shù)不會超過N2，所以可以采用哈希將二維的點映射到一位數(shù)組中。每個點記錄水平走廊的編號。
2、豎直線段
同上操作，不同的是每個點記錄豎直走廊的編號。
經(jīng)過1和2兩步操作后，走廊上的關(guān)鍵點已經(jīng)被離散化了，并且所有點都通過四向鏈表串接起來，然后只需要從起點開始模擬行走即可，走到一個關(guān)鍵點，將關(guān)鍵點所在的兩個走廊編號標(biāo)記掉，最后統(tǒng)計沒有標(biāo)記的走廊編號就是答案了。
D. City Game
PKU 1964 http://poj.org/problem?id=1964
題意：給定一個M*N(M <= 1000，N <= 1000)的01矩陣，求它的一個子矩陣，滿足矩陣元素全為1，并且面積最大。
題解：枚舉行，對于第i行，以第i行為起點，掃描每一列j，找到第一個不是1的數(shù)所在的位置P[j]，令K[j] = P[j] - i，于是問題轉(zhuǎn)化成了一個一維的問題。
L[i] 表示 K [ L[i]+1 ... i] 中的元素都大于等于K[i]，但是L[i]小于K[i]；
R[i] 表示 K [i ... R[i]-1] 中的元素都大于等于K[i],但是R[i]小于K[i]；
Max{ (R[i] - L[i] - 1) * K[i], 1 <= i <= N }就是以當(dāng)前枚舉行為起點的最大矩陣，枚舉M次取最大值就是全局的最大子矩陣了。
E. Cube Root
PKU 1965 http://poj.org/problem?id=1965
題意：給定一個不超過150個數(shù)字的正整數(shù)，求它的三次方根，精確到小數(shù)點后10位。
題解：大數(shù)模擬
將輸入的數(shù)X用字符串存儲，乘上1030，利用二分求出最大的Y，使得Y3 <= X。然后在Y的后十位前插入一個小數(shù)點，輸出即可。
F. Cable TV Network
PKU 1966 http://poj.org/problem?id=1966
題意：求圖的點連通度。給定一個N(N <= 50)個點的圖，求去掉至少多少個點能夠?qū)⑺兂梢粋€非連通圖。
題解：搜索 + 剪枝 (或者 最大流)
枚舉每個點去掉或不去掉，總共250種狀態(tài)，每次去掉點后判斷當(dāng)前圖的連通性，一旦破壞了連通，去掉的點數(shù)即為答案；如果發(fā)現(xiàn)某個點去掉后，剩下點組成的圖變成了一個完全圖，那么不用繼續(xù)搜索了，因為當(dāng)前狀態(tài)下不可能將剩下的圖變成非連通圖了；如果去掉的點數(shù)超過目前的最優(yōu)解也直接剪枝。
好吧...一定是數(shù)據(jù)弱了-_-||，正解是最大流拆點。
G. Alibaba
PKU 1967 http://poj.org/problem?id=1967
題意：給定N(N <= 104)個整數(shù)對(Pi, Di)表示在Pi位置有一個寶物，并且需要在Di 時間之前取走(給出順序為Pi遞增的順序)。起始可以任意選擇一個位置，往左或者往右取寶物，問是否能夠保證每個物品都在Di時間之前取走(時間和距離關(guān)系為1:1)，如果可以，給出取完所有寶物的最少時間。
題解：搜索 + 剪枝
首先可以想到的是，起始位置一定是N個寶物所在位置中的其中一個，所以首先可以枚舉每個寶物的起始點，比如當(dāng)前位置為pos，那么在第0秒內(nèi)，訪問過的區(qū)間為[pos, pos]，可以選擇往左走，也可以選擇往右走，那么是不是只要選擇某個方向走完，然后再反方向走到底如果能夠滿足所有點都在截止時間內(nèi)完成一定是對的呢？答案是否定的，來看一組數(shù)據(jù)，如圖1，起始點只能選擇3號位置，并且只能選擇往右走，走到4后再折回走到2，然后再折回走到5，以此類推，并且只有這一種路徑才能滿足所有寶物都在截至?xí)r間內(nèi)取完。
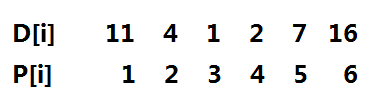
圖1
按照這個思路，進行狀態(tài)的劃分，假設(shè)當(dāng)前已經(jīng)訪問的區(qū)間為[L, R]，并且現(xiàn)在的位置處于pos位置(這里pos要么等于L，要么等于R)，所以可以用三維來表示狀態(tài)DP[s][l][r](l、r表示訪問過的區(qū)間的左右端點，如果當(dāng)前位置在l則s = 0，如果當(dāng)前位置在r，則s=1)，總共狀態(tài)數(shù)目N2，狀態(tài)轉(zhuǎn)移的時候由大狀態(tài)推小狀態(tài)，即DP[s][l][r]一定是由DP[0][l-1][r]、DP[0][l][r+1]、DP[1][l-1][r]、DP[1][l][r+1]這四個狀態(tài)得出。
考慮到N比較大，所以把所有狀態(tài)存儲到數(shù)組中再利用動態(tài)規(guī)劃進行遞推，如果數(shù)據(jù)量不多的話，可以卡過，但是狀態(tài)存儲需要用滾動數(shù)組，否則內(nèi)存吃不消，也可以采用搜索 + 剪枝，思路是沿用了動態(tài)規(guī)劃的思想，假設(shè)當(dāng)前已經(jīng)訪問的區(qū)間為[L, R]，現(xiàn)在的位置處于pos位置(這里pos要么等于L，要么等于R)，并且已經(jīng)使用了T的時間，無論當(dāng)前的pos是在左區(qū)間端點L上還是在右區(qū)間端點R上，他都可以選擇走到L-1(L > 1)，或者R+1(R < N)，于是就可以遞歸求解了，遞歸出口為L=1，R=N的時候。
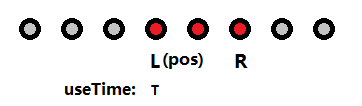
圖2
如圖，已經(jīng)訪問的寶物為紅色標(biāo)記的點，灰色標(biāo)記的為未曾訪問過的，并且現(xiàn)在的位置在已經(jīng)訪問區(qū)間的左端點L上，已經(jīng)使用了T的時間，我們需要判斷這個狀態(tài)是否合法，則需要滿足以下的幾個不等式。
1、保證右邊未訪問的都能在截止時間內(nèi)訪問到：
T + (P[R] - P[L]) + (P[R+1] - P[R]) < D[R+1]
T + (P[R] - P[L]) + (P[R+2] - P[R]) < D[R+2]
...
T + (P[R] - P[L]) + (P[N] - P[R]) < D[N]
將這些等式化簡，可得：
T - P[L] < D[R+1] - P[R+1]
T - P[L] < D[R+2] - P[R+2]
...
T - P[L] < D[N] - P[N]
再進行進一步化簡，得：
T - P[L] < Min{ D[k] - P[k], R < k <= N }
2、保證左邊未訪問的都能在截止時間內(nèi)訪問到：
同理，可以得出：
T + P[R] < Min{ D[k] + P[k], 1 <= k < R }
那么，令 POSTM[i] = Min{ D[k] - P[k], i < k <= N }
PREM[i] = Min{ D[k] + P[k], 1 <= k < i }
這兩個數(shù)組可以分別通過一次逆序和順序的線性掃描求出來，用于搜索的時候判斷可行性。例如，當(dāng)T - P[L] >= POSTM[R] 表示在右邊未訪問的寶物中有至少一個寶物不能在截止時間前被訪問到，T + P[R] >= PREM [R]表示在左邊未訪問的寶物中有至少一個寶物不能在截止時間前被訪問到，直接剪枝。
還需要一個剪枝，就是在當(dāng)前時間T加上當(dāng)前狀態(tài)下預(yù)計訪問完所有寶物的最小時間已經(jīng)比之前求出的最小時間大，直接剪枝。
H . Booklets
PKU 1968 http://poj.org/problem?id=1968
題意：N(N <= 3000)本小冊子需要分配給S個學(xué)校，每個學(xué)校得到的是N/S的上整本冊子或者N/S的下整本冊子，每本冊子有一個頁數(shù)，并且規(guī)定分配冊子的時候按照頁數(shù)遞增來分配，先把上整本冊子分完再分下整的，對于每個學(xué)校的分書規(guī)則，按照輸入的順序進行分配。求問第T個學(xué)校分到的第一本冊子的頁數(shù)。
題解：需要求出幾個量：
上整冊子的數(shù)目UIP = (N+S-1) / S;
下整冊子的數(shù)目LIP = N/S;
分到上整冊子數(shù)目的學(xué)校個數(shù)UIPC = N % S;
分到下整冊子數(shù)目的學(xué)校個數(shù)LIPC = N - N % S;
首先對所有的冊子按頁數(shù)遞增來排序(如果頁數(shù)相同按照下標(biāo)遞增排序)，然后減去前T-1個學(xué)校的冊子總數(shù)，容易得出第T個學(xué)校分到的冊子數(shù)目C，從接下來的C個冊子中找到之前下標(biāo)最小的冊子，它對應(yīng)的頁數(shù)就是答案。
I. Count on Canton
PKU 1969 http://poj.org/problem?id=1969
題意：給定下圖所示的無限分?jǐn)?shù)序列，并且按照蛇形方式編號，即第一個為1/1，第二個為1/2，第三個為2/1，第四個為3/1，以此類推，問第N個分?jǐn)?shù)是什么。
1/1 1/2 1/3 1/4 1/5 ...
2/1 2/2 2/3 2/4
3/1 3/2 3/3
4/1 4/2
5/1
題解：數(shù)學(xué)題。
首先二分求出在第幾條斜線上，即(K-1)K/2 < N的最大的K，然后求根據(jù)K的奇偶性求出蛇形在第K條斜線的行走方向，第N - (K-1)K/2 個數(shù)就是答案。