140 Integer Sequences 數論:擴展歐幾里得
141 Jumping Joe 枚舉142 Keyword 搜索:IDA*
143 Long Live the queen 動態規劃:樹形DP
144 Meeting 數學:概率題
145 Strange People 搜索:啟發式搜索
146 The Runner 數學題
147 Black-white king 區間求交
148 B-station 枚舉:堆優化
149 Computer Netowrk 動態規劃:樹形DP
140 Integer Sequences
線性同余(模方程組)
題意:給定數組A( A[i] <= 2*109 ),求非負整數數組X,使得 (A*X) MOD P == B。
題解:根據題意,對于數組A,X,個數N以及除數P和余數B,可得
(
A[0]*X[0] + A[1]*X[1] + A[2]*X[2] + ... + A[N-1]*X[N-1] ) MOD P = B (1)
稍微做一下變形,可得(2)式:
(
A[0]*X[0] + A[1]*X[1] + A[2]*X[2] + ... + A[N-1]*X[N-1] ) + K * P = B (K為任意整數) (2)
由于K為任意整數,所以我們可以將它拆成K0 + K1 + K2 ... + KN-1,然后分別和前面N項去匹配,得到下面的等式:
(A[0]*X[0]
+ K0*P) + (A[1]*X[1] + K1*P)
+ ... + ... (A[N-1]*X[N-1] + KN-1*P) = B (3)
根據擴展歐幾里得定理,ax + by =
GCD(a, b) 必定有整數解,于是(3)式可以轉化為
GCD(A[0],
P) * T0 + GCD(A[1], P) * T1 + ... + ...
GCD(A[N-1], P) * T N-1 =
B (4)
令A'[i] = GCD(A[i],
P), X'[i] = Ti,(4)可以簡化為
A'[0]*X'[0]
+ A'[1]*X'[1] + A'[2]*X'[2] + ... + A'[N-1]*X'[N-1] = B (5)
這時我們可以發現,(2)和(5)的形式是一樣的,只不過(2)有N+1項,(5)有N項,所以根據數學歸納法,進過N次操作之后,最后的等式必定可以轉化成
ax = B 的形式,這里的a為所有A[i]的GCD,這個x當且僅當a整除B的時候有解,然后根據x的值可以遞推求出上一層的值,經過N次迭代就可以將所有的X[i]求出來了。
注意:迭代過程中,各種乘法有可能會整數越界,所以每次計算出的結果要對P求余,如果值小于零需要再加上P。
141 Jumping Joe 枚舉
題意:求滿足方程組
P1*x1 - N1*x1 + P2*x2 - N2*x2 = P
P1 + N1 + P2 + N2 = K
的正整數解(P1 , N1, P2, N2)。x1, x2 (0 < x1 , x2 < 40 000), P (-40 000 < P < 40 000) and K(0 <= K < 2*109)
題解:首先將第一個方程變一下形,可以發現:
(P1 - N1)x1 + (P2 - N2)x2 = P 其實是一個模線性方程,而P的范圍很小,所以可以考慮枚舉(P1 - N1)的值,枚舉范圍為[-40 000, 40 000]。如果在這個范圍內找不到解,那么在更大的范圍必定也找不到解。
所以令a = P1 - N1,
1)如果 (P - a*x1) mod x2不等于零,則說明這個枚舉的a非法,因為P2 - N2必須為整數;
2)否則,b = P2 - N2 = (P - a*x1) / x2;
3)a + b = (P1 + P2) - (N1 + N2)
K = (P1 + P2) + (N1 + N2)
所以如果 a+b 和 K的奇偶性必須保持一致,否則說明枚舉的a非法,繼續枚舉下一個;
4)令 c = P1 + P2 = (a+b+K)/ 2
5)將四個未知數用P1來表示:
a) P1 = P1
b) P2 = c - P1
c) N1 = P1 - a
d) N2 = c - b - P1
由于四個未知數都是非負整數,所以有
a) P1 <= c
b) P1 >= a
c) P1 <= c - b
d) P1 >= 0
那么P1 的左區間為 Max(a, 0), 右區間為Min(c, c - b),如果左區間小于右區間,則當前枚舉的a無解,否則說明找到一個可行解,P1直接取Max(a, 0), 就可以順勢算出N1、P2、N2的值了。
142 Keyword
IDA* + HASH
題意:給定一個長度為N(N <= 5*105)的字符串T(只包含'a'或'b'),求一個最短的字符串S(只包含'a'或'b'),并且S不是T的子串。
題解:可以這么考慮,對于一個長度為N的串,它有長度為L的子串(1
<= L <= N),這種子串的個數為X = N - L + 1, 理論上最大允許的子串種數為 Y = 2L。則 Z = Y - X = 2L -
(N - L + 1) = 2L + L - N - 1, 可得Z為對于自變量L的增函數,當L
= N 的時候 Z = 2N - 1 > 0, 所以實際最大子串種數會遠遠高于出現的子串數,于是可以通過枚舉子串的長度L,然后利用深搜枚舉每一位是'a'還是'b',當枚舉完畢一個長度為L的子串后判斷是否是原串的子串,如果不是則直接輸出解,結束搜索過程。否則繼續枚舉下一個,當所以長度為L的子串枚舉完畢都沒有找到解,則枚舉L
+ 1的情況。
由于每個字符串只有'a'和'b'兩種字符,所以可以將每個字符串壓縮成一個二進制的整數,例如: aab 可以表示為 001, bbbaa可以表示為
11100,以此類推...
判斷是否是子串的操作也可以不需要進行字符串逐個比較,只要在枚舉之前對源字符串的所有長度為L的子串進行一次哈希,然后枚舉完畢在哈希數組中查找是否出現即可,每次查找復雜度O(1)。
長度為 500000,結果少看了一個0,將數組開成了
50000,悲劇...;
143 Long Live the Queen
動態規劃(樹形DP)
題意:給定一顆樹,和樹上每個結點的權值,求一顆子樹,使得權和最大。
題解:用DP[1][i] 表示i這個點選中的情況下,以i為根的子樹的權和最大值;
用DP[0][i]表 示i這個點不選中的情況下,以i為根的子樹的權和最大值;
DP[1][i] = v[i]
+ sum{ DP[1][v] v是i的直接子結點 && DP[1][v] > 0 }
DP[0][i] = max(
0, max{ max( DP[0][v], DP[1][v] ), v是i的直接子結點 } )
這樣,構造一個以1為根結點的樹,然后就可以通過dfs求解了。這題題目要求求出的樹為非空樹,所以當所有權值都為負數的情況下需要特殊處理,選擇所有權值中最大的那個作為答案。
144 Meeting
概率題
題意:A和B兩個人想要在(X,Y)這個時間段內見面,但是如果某個人先來,他等的時間超過了Z,他就會走,他們就見不到面了。問他們能見面的概率。
題解:面積法。畫個圖就明白了。
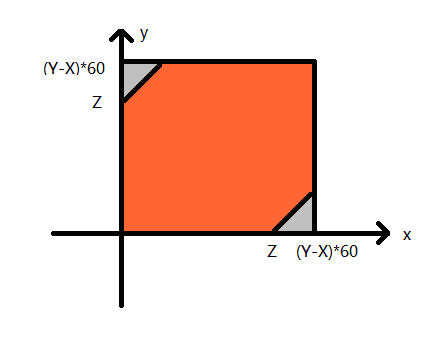
圖1
x軸表示A出現的時間,y軸表示B出現的時間,平面坐標的點表示他們出現時間的集合,只有當點在橙色區域內,才能相遇。假設A在t1時刻出現,B在t2時刻出現,那么
只有當 |t1 - t2| <= Z 時才可能相遇,將不等式化簡就可以得到上圖,所以最后的概率就是圖中的六邊形區域面積 除上 正方形的面積。
即:
A = 60 * (Y - X)
B = 60 * (Y-X) - Z
P = 1 - B*B / (A*A)
145 Strange People
啟發式搜索
題意:給定N(N<=100)個點和M(M
<= N*(N-1))條單向邊,以及起點S和終點T,求從S到T的第K(K <= 500)短簡單路(每個點只能訪問一次)。
題解:首先,利用反向邊求出終點T到所有點的最短路d[i],那么d[S]表示從S到T的最短路。令maxLength =
d[S],然后利用dfs搜索從S到T,長度不超過maxLength的簡單路徑,如果找到的路徑總數大于等于K,則結束搜索,這時的maxLength表示第K條路徑的長度;否則增大maxLength的值,重復上述步驟,直到maxLength為無窮大都找不到K條路徑的時候就表示沒有第K短路。
在進行搜索的時候,需要加上一些剪枝:
1) 可達性剪枝
假設當前訪問到的點為u,之前已經訪問過的點的集合為vset。那么利用BFS可以在O(n)的時候內判斷u到T是否可以在不經過vset的情況下可達。
2) 啟發式剪枝
假設當前訪問到的點為u,本次搜索中從S到u的距離已知,為length(S,
u),而之前已經計算出從u到T的最短估計距離為d[u](即A*中的估價函數,之所以稱之為估價,是因為它并不是真正的最短距離,因為在S到u這條路徑上可能訪問了u到T這條最短路徑上的點,所以真正的最短距離肯定大于等于d[u])。如果length(S, u) + d[u] > maxLength,則表明當前這種策略中,從S經過u到達T的最短距離已經大于給定的長度,就不用往下搜索了。
在搜索的過程中,每次搜索到某個點u的時候都可以找到一個值vLength
= length(S, u) + d[u],我們取所有vLength中滿足大于maxLength 的值的最小者作為下一次搜索時的最大長度maxLength,使得maxLength不是以每次加1的方式累加,從而減少了很多不必要的枚舉,可以大大加快找到第K短路的速度。
3) 二次啟發剪枝
啟發式剪枝可以解決大多數隨機數據,但是對于某些特殊設計的數據,還是得想更好的剪枝,例如圖2所示,起點為S,終點為T,除了起點和終點,其它點形成一個完全圖,邊的權值均為1。如果采用上面的方法進行啟發,最短路d[S]為2,次短路則為10000+1+1 = 10002,但是除了終點以外,任何一個點到達T的最短路都是2,即d[i] = 2 (i
!= T),這意味著length(S, u) + d[u]不能很好的起到啟發的作用,會讓maxLength還是以加1的方式逐漸累加,然后就有可能出現這種情況:從S出發,進入到完全圖中走了一大圈,然后到達和T相連的那個點發現邊權值為10000,遠大于maxLength,但是這個狀態圖是N!的復雜度,等到搜索結束估計花兒都謝了...
可以用d[i][j]來保存從j點到達終點T,并且不經過i點的最短路徑,同樣可以通過從T點反向一次預處理求得。然后每次訪問到u的時候,判斷從S到u之間的點中,是否有滿足length(S, u) + d[v][u] > maxLength的v,如果存在,直接剪枝,并且用最小的length(S,
u) + d[v][u]作為下一次的啟發值。
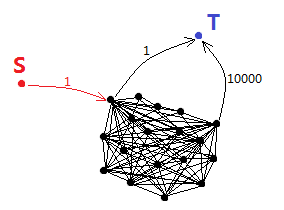
圖2
146 The Runner
精度轉化題
題意:一個人在一個周長為L的圓上跑,每個時間段(Ti)的速度(Vi)不一樣,問最后他離起點的圓弧距離,周長是個有四位小數的浮點數,其它全是整數。
題解:首先可以考慮如果周長是整數的話,就可以通過取余來求解了,而周長最多只有四位小數,所以可以考慮將周長和(Ti, Vi)都擴大10000倍,全部轉化成整數后,只要將總距離Sum{ Ti
* Vi } 模上周長取余數即可。
注意,這里是圓弧,圓弧是有一個優弧和劣弧的概念的,所以要取兩條弧之間的最小值。
147 Black-white king
區間求交
題意:在一個N*N(N <= 106)的棋盤上,有三個棋子:黑王、白王、黑白王,它們的行走方式一致,每秒向8個方向中的任意一個行走一步,如圖3所示。
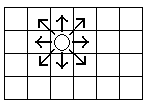
圖3
現在黑王和白王想要相遇(即占據相鄰的格子),而黑白王需要阻止它們相遇,即抓住其中一個王(走到其中一個王所在的格子),黑王和白王行走時總是走最短路徑,而黑白王走的路徑無法被縮短(即能夠走斜向的時候,不會走Z字形),由于黑白王是隱身的,所以黑王和白王無法看見黑白王的走向,但是他們知道有它存在,當黑王和白王走到黑白王所在的格子時不會有任何事情發生。問黑白王是否有可能抓住其中一個王,如果有可能,輸出最少步數;如果不可能,輸出黑王和白王相遇總共的行走步數。行走順序為白王、黑王、黑白王。
題解:
如果黑王和白王的y方向差值小于x方向差值,那么將三個棋子的x和y值分別交換。保證黑王和白王的y方向差值大于等于x方向差值,由于黑王和白王總是走他們能夠相遇的最短路徑,所以每次移動一定要保證在y方向朝對方移動一格,所以兩個王的行走區域為朝著對方方向的一個“喇叭”形區域。
如圖2所示,兩個王的y方向坐標差值為T,黑王坐標(Bx, By),白王坐標(Wx, Wy),那么走i步后的黑王的y方向坐標為定值By + i * bDir,其中bDir為黑王到白王的方向;x方向的可行區間為[Bx – i, Bx + i]和[Wx – (T-i), Wx + (T-i)]的區間交集,即圖中兩個“喇叭”形區域的交集就是黑王和白王的可行區域,最多T-1步后兩人相遇。
圖4
黑白王的運動區域更加簡單,如圖3所示,灰色的方形外框表示經過3步后黑白王有可能在的位置,即一個長度為2i + 1的空心正方形區域。
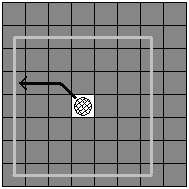
圖5
于是,可以枚舉步數,判斷黑王和黑白王、白王和黑白王的第i步的區間區域是否有交集,如果一旦出現某個王在第i步的時候和黑白王的正方形區域有交集,則表明黑白王有可能在第i步抓住其中一個王,否則當2i >= T-1的時候還沒有交集,表明黑王和白王已經相遇,總步數為T-1。總復雜度O(N)。
148 B-Station
枚舉 + 堆優化
題意:給定N(N <= 15000)個工作車間,每個工作車間有Wi的水量,能承受Li的水量,如果水量超過Li,第i個車間的所有水就會盡數流入第i+1個車間,同樣,摧毀第i個車間,那么它的水量也會流入第i+1個車間,但是摧毀第i個車間是有代價Pi的,現在問要讓第N個車間的水全部流出來,最小的代價是多少。
題解:首先,暴力的辦法就是枚舉第一個被摧毀的車間k,如果存在i使得Wk + Wk+1 +
... + Wi <= Li,那么第i個車間必須也要被摧毀(否則經過第i個車間流不過去,前面的努力就白費了呀),這樣就可以把所有需要摧毀的車間枚舉出來,比較最小值,復雜度O(N2),對于15000的數據量來說是行不通的。
那么突破口在哪里呢?還是枚舉的思路,假設我們現在從第一個車間開始摧毀,模擬水流往下流,記錄所有需要摧毀的車間集合S;那么當我們枚舉第二個車間開始摧毀的時候,需要摧毀的車間集合T一定是包含了 S - {1}
的;同樣,第三個車間開始摧毀的時候,摧毀的車間集合一定是包含了T - {2}的,原因很簡單,起始摧毀車間編號越大,流經某個車間時候的總水流就越小,超過下限的機會越少,越有可能要進行人為的摧毀。為了便于理解,先來看一組數據:
W
L P SumW
SumW - L
1
6
5 1 -5
2
8
3 3 -5
3 4 9
6 2
4 2 7
10 8
3 12 5
13 1
5 15
4 18 3
我們用SumW[i]記錄從第1個到第i個車間的水流總和,SumW[i] - L[i]則表示當選定第一個車間摧毀后,水流流經第i個車間后剩余的水量,很明顯,當這個剩余水量小于等于0的時候,表明這個車間也要被摧毀,所以在上面這個例子中,如果選定了第一個車間摧毀,那么第二個車間也必須被摧毀。
那么,如果選定第二個車間為起始摧毀車間,其實就是在 { SumW[i] - L[i]-W[1] | i >= 2 }這個集合中找小于等于0的數的下標,于是,算法也就應運而生了。
用preCost記錄枚舉第k個為起始摧毀車間的最小花費,一個小頂堆RQ存放SumW[i] -
L[i]的值,另外一個小頂堆CQ存放此次的摧毀車間集合,那么當枚舉到第k+1個車間的時候:
1) 判斷RQ堆頂元素WL;
a) 如果 WL.val -
SumW[k] <= 0 說明第WL.idx個車間需要被摧毀,彈出WL,將 花費累加到preCost上,繼續1)。
b) 否則,其他車間均無須摧毀,轉到2)(因為這是一個小頂堆,如果某個WL.val - SumW[k] > 0,那么以后彈出的元素至少不會比這個小)。
2) 判斷CQ堆頂元素idx;
a) 如果 idx 下標比k+1小,那么彈出idx,將花費從preCost中減去,繼續2)。
b) 否則,此時CQ中的元素為當次枚舉說需要摧毀的車間,轉3);
3) 將花費 preCost 和最小花費 MinCost 比較,更新最小花費。
這樣一來,每個車間最多進隊一次,出隊一次,插入、彈出復雜度均為O( log(N) ),所以整個算法復雜度為 O( N log(N) )。
149 Computer Network
動態規劃(樹形DP)
題意:給定一棵樹,求這棵樹上每個結點的最長路。
題解:
DP[0][i] 表示以i為根結點的子樹 中 i到葉子結點的最長路。
Pre[0][i] 表示導致此次最長路的結點編號。
DP[1][i] 表示以i為根結點的子樹 中 i到葉子結點的次長路。
Pre[0][i] 表示導致此次最次路的結點編號。
從根結點開始遍歷,對于每個結點,
DP[0][i] = max{
edge(i, son) + DP[0][son] son 為i的直接子結點 }
同時保存下
最長路 產生的子結點的編號 Pre[0][i];
DP[1][i] = max{
edge(i, son) + DP[0][son] son !=
Pre[0][i] son 為i的直接子結點 }
同時保存下
次長路 產生的子結點的編號 Pre[1][i];
LN[0][i] 表示i到所有點中的最長路。
LN[1][i] 表示i到所有點中的次長路。
然后對于根結點1再進行一次結點遍歷,更新LN[0][i]和LN[1][i]的值;
顯然,LN[0][i] >= DP[0][i]; LN[1][i] >= DP[1][i](因為DP表示子結點過來的最長路,而LN則包含了從父親結點過來的最長路,所以計算LN一定要先計算i的父親u的最長路和次長路)。
所以從1開始,1的最長路和次長路和次長路一定是等于子結點過來的值(因為1為根結點,沒有父親)。然后遍歷1的子結點,每次遍歷結點u,更新兒子v的最長路以及次長路(包括導致此次路徑的前驅編號Pre):
1) 選取待定最長路;
a) 如果u的最長路來自v,那么待定最長路為 T = LN[1][u]
+ edge(u, v)
b) 如果u的最長路不來自v,那么待定最長路為 T = LN[0][u] + edge(u, v)
2) 將待定最長路和原本v到子結點的最長路、次長路進行比較;
a) 如果待定最長路T 比v本身的最長路LN[0][v]要長,那么:
LN[1][v] = LN[0][v]; // 原本最長路變為次長路
LN[0][v] = T; // 更新原來的最長路為待定最長路
b) 如果待定最長路T 比v本身的次長路LN[1][v]要長,那么:
LN[1][v] = T; // 更新原來的次長路為待定最長路
3) 比較的時候需要將前驅編號也保存下來,因為每次選取待定最長路的時候需要用前驅編號來判斷是選最長路還是選次長路。