AABB與平面的相交性檢測
考慮3D中由極值點(diǎn)pmin和pmax定義的AABB和以標(biāo)準(zhǔn)方式定義的平面：p
. n = d，其中n為單位向量，平面與AABB必須處于相同的坐標(biāo)系中。
一種簡單的靜態(tài)測試方法是，計(jì)算矩形邊界框頂點(diǎn)和n的點(diǎn)積，通過比較點(diǎn)積和d，來檢測邊界框的頂點(diǎn)是否完全在平面的一邊，或是在另外一邊。如果所有點(diǎn)積都大于d，那么整個(gè)邊界框就在平面的正面所指的一側(cè)；如果所有的點(diǎn)積都小于d，那么整個(gè)邊界框就在平面的反面所指的一側(cè)。
實(shí)際上，不需要檢測全部的8個(gè)頂點(diǎn)，可以用和變換AABB類似的技巧，例如，如果nx
> 0，點(diǎn)積最小的頂點(diǎn)是x = xmin，點(diǎn)積最大的頂點(diǎn)是x= xmax。如果nx
< 0，則得出的是相反的結(jié)論。對(duì)ny、nz也有同樣的結(jié)論。我們計(jì)算最小和最大點(diǎn)積的值，如果最小點(diǎn)積大于d或最大點(diǎn)積小于d，說明它們不相交；否則，兩個(gè)點(diǎn)在平面的兩邊，說明邊界框與平面相交。
接下來進(jìn)行動(dòng)態(tài)測試，我們假設(shè)平面是靜止的（以一個(gè)移動(dòng)物體為參考來考慮它們的相交性檢測會(huì)比較簡單）。邊界框的位移由單位向量d和長度L定義，和前面一樣，先求得點(diǎn)積最大和最小的頂點(diǎn)，并在t=0時(shí)作一次相交性檢測，如果邊界框和平面最初沒有相交，那么一定是離平面最近的頂點(diǎn)先接觸平面，它可能就是前一步檢測出的兩個(gè)頂點(diǎn)之一。如果只對(duì)與平面的"正面"碰撞感興趣，那么總是使用點(diǎn)積最小的頂點(diǎn)。一旦檢測出先接觸到平面的頂點(diǎn)，就可以利用射線與平面的相交性測試來解決問題。
cAABB3類實(shí)現(xiàn)了AABB與平面的靜態(tài)、動(dòng)態(tài)相交性檢測。
三個(gè)平面間的相交性檢測
在3D中，三個(gè)平面相交于一點(diǎn)，如圖13.7所示:
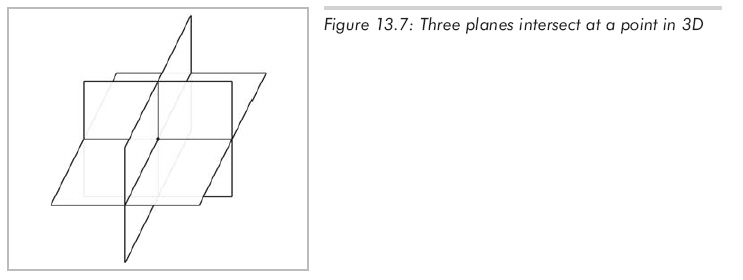
假設(shè)三個(gè)平面的隱式方程為：
p . n1 = d1
p . n2 = d2
p . n3 = d3
雖然平面的法向量通常被限制為單位向量，但此時(shí)這種限制是沒有必要的。上面的等式組成了一個(gè)有三個(gè)方程和三個(gè)未知數(shù)（交點(diǎn)的x、y、z坐標(biāo)）的線性方程組。解這個(gè)方程組能得到如公式13.7所示的結(jié)果：
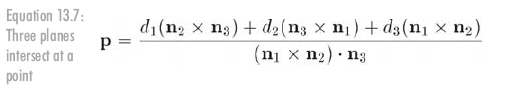
如果任意一對(duì)平面平行，那么交點(diǎn)要么不存在，要么不唯一，在這種情況下，公式13.7的分母都為0。
射線和圓/球的相交性檢測
這里將討論2D中射線和圓的相交性檢測，檢測的方法也適用于3D中射線和球之間的相交性檢測，這是因?yàn)榭梢栽诎渚€和球心的平面中進(jìn)行檢測，從而將3D問題轉(zhuǎn)化為2D問題。（如果射線包含在穿過球心的直線上，那么這個(gè)平面就不是唯一的。但這并不是問題，在這種情況下我們能使用任意包含射線和球心的平面來進(jìn)行計(jì)算。）
構(gòu)圖方法見13.8 :
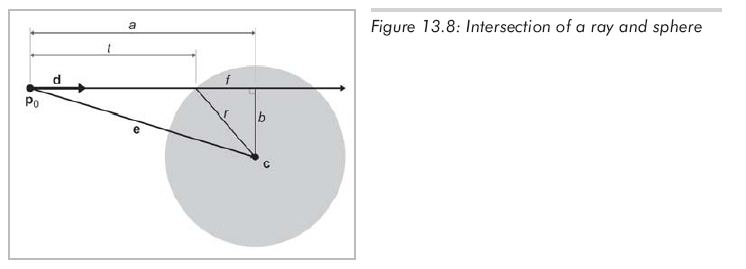
用圓心c和半徑r來定義球，射線的定義為：p(t)
= p0 + td
這里，d為單位向量，t從0變化到L，L為射線長度。所要求的是交點(diǎn)處t的值：
t = a - f
a的計(jì)算方法如下，設(shè)e為從p0指向c的向量:
e = c - p0
現(xiàn)在將e投影到d，這個(gè)向量的長度為a，它的計(jì)算式為：
a = e . d
兩個(gè)圓/球的相交性檢測
兩個(gè)球的靜態(tài)測試是相對(duì)比較簡單的（這里的討論對(duì)圓也適用，事實(shí)上，圖13.9中用的就是圓）?？紤]由球心c1、c2和半徑r1、r2定義的兩個(gè)球（如圖13.9所示）。設(shè)d為球心間的距離，很明顯，當(dāng)d
< r1 + r2時(shí)它們相交。在實(shí)踐中通過比較d2
< (r1 + r2)2，可以避免包括計(jì)算d在內(nèi)的平方根運(yùn)算。
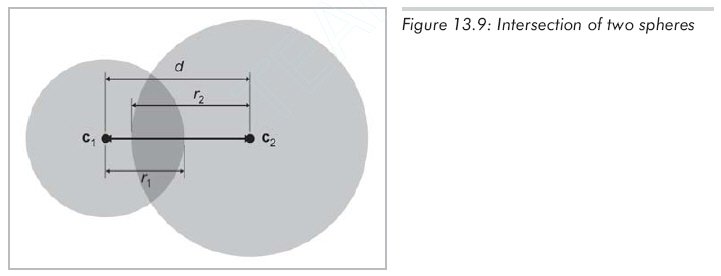
對(duì)兩個(gè)運(yùn)動(dòng)的球進(jìn)行相交性檢測要麻煩一些。假設(shè)有兩個(gè)單獨(dú)的位移向量d1和d2，球與位移向量是一一對(duì)應(yīng)的，它們描述了在所討論的時(shí)間段中球的運(yùn)動(dòng)方式。如圖13.10所示:
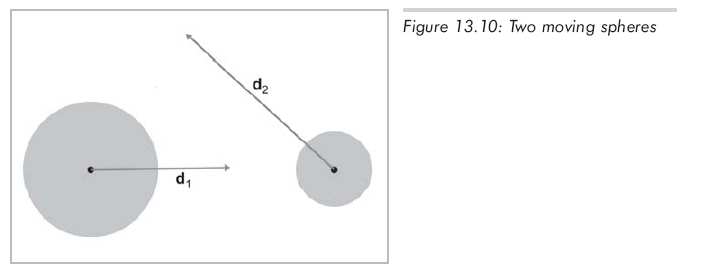
從第一個(gè)球的角度來看能夠簡化這個(gè)問題，現(xiàn)在假設(shè)這個(gè)球是"靜止的"，另一個(gè)球是"運(yùn)動(dòng)"的。這給出了單一的位移向量d，它等于原位移向量d2和d1的差d2
- d1，如圖13.11所示：
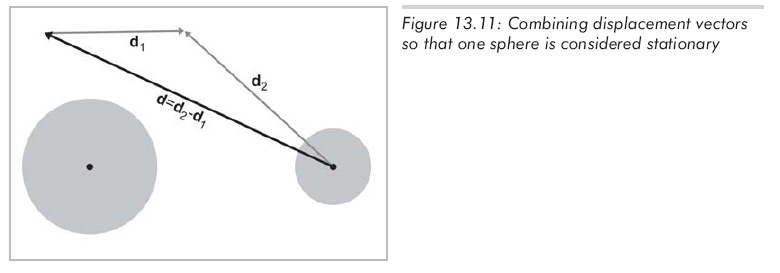
設(shè)靜止球由球心cs和半徑rs定義。運(yùn)動(dòng)球的半徑為rm，當(dāng)t=0時(shí)，球心為cm。t不再從0變化到1，而是將d單位化，t的取值范圍從0到L，L是移動(dòng)的距離。所以在t時(shí)刻運(yùn)動(dòng)球的球心為cm
+ td，所要求的是當(dāng)運(yùn)動(dòng)球接觸靜止球時(shí)的t。其中的幾何關(guān)系如圖13.12所示：
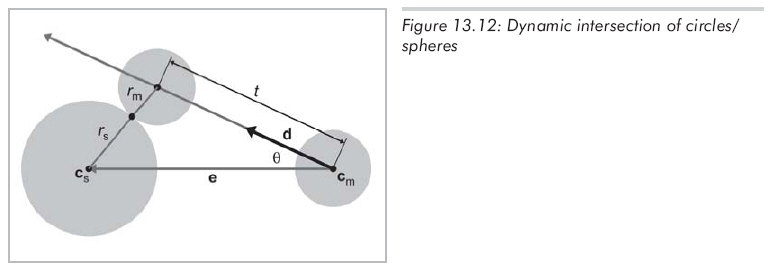
這里有一些重要的注意事項(xiàng)：
（1）如果||e|| < r，則球在t=0時(shí)就相交。
（2）如果t<0或t>L，那么在所討論的時(shí)間段內(nèi)兩個(gè)球不會(huì)發(fā)生接觸。
（3）如果根號(hào)內(nèi)的值是負(fù)的，那么兩個(gè)球不會(huì)相交。
球和AABB的相交性檢測
為了進(jìn)行球和AABB的靜態(tài)相交性檢測，首先找到AABB中距球心最近的頂點(diǎn)。計(jì)算該點(diǎn)到球心的距離，并和球的半徑比較（實(shí)際上，比較的是距離的平方和半徑的平方，以避免平方根運(yùn)算）。如果距離小于半徑，那么球和AABB相交。