在這一部分我們關注的焦點是數學中的矩陣。它們在3D圖形學中的應用將在下一部分講解。
一個m×n的矩陣是由m行和n列的數字組成的矩陣列。行和列的數字就是這個矩陣的維數。我們通過寫在下方的數字識別矩陣清單,數字中的第一個表示行第二個表示列。例如下邊的M是3×3矩陣,B是2×4矩陣,
C是3×2矩陣。
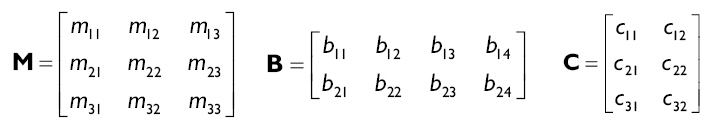
我們使用加粗的大寫字母表示矩陣。有時一個矩陣只包含一行或者一列。我們用行矩陣和列矩陣這個特殊的名稱來稱呼。例如下邊就是行和列矩陣:
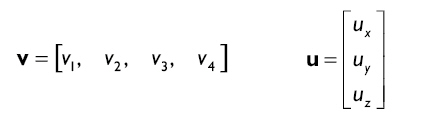
當使用行或列矩陣時,我們只用一個下標,有時我們還用字母表示。




當設計Direct3D應用程序時,使用4×4矩陣和1×4行矩陣(向量)是有代表性的。注意使用這兩種矩陣意味著可以進行下列定義的矩陣乘法。
n
向量-矩陣乘法。即,假如1×4的單行矩陣V,和4×4的矩陣T,那么積VT可計算并且返回的結果是一個1×4的單行矩陣(向量)。
n
矩陣-矩陣乘法。即,假如4×4的矩陣T,和4×4的矩陣R,那么積TR和RT可計算并且兩者返回的結果都是一個4×4的矩陣。注意因為矩陣乘法不滿足交換律所以TR和RT不一定相等。
在D3DX中表示1×4的行矩陣(向量),我們用D3DXVECTOR3和D3DXVECTOR4向量類。當然D3DXVECTOR3只有3個成員,不是4個。然而,第4個成員缺省是1或0(在下一部分有更多信息)。
在D3DX中表示4×4的矩陣,我們用D3DXMATRIX類,定義如下:
The D3DXMATRIX class
inherits its data entries from the simpler
D3DMATRIX structure, which is defined as:
觀察D3DXMATRIX類發現有很多有用的運算符,比如對矩陣檢測相等,矩陣相加和矩陣相減,標量與矩陣相乘,類型轉換(casting),以及非常重要的兩個D3DXMATRIXs相乘。因為矩陣相乘是非常重要的,我們給出一段實例代碼:
|
D3DXMATRIX A(…);
// initialize A
D3DXMATRIX B(…);
// initialize B
D3DXMATRIX C = A * B;
// C = AB
|
D3DXMATRIX類另一個重要的運算符是小括號,它允許我們非常方便的為矩陣成員賦值。注意當使用小括號時我們的下標就象C語言數組下標一樣是從0開始的。例如,為一個矩陣的ij
= 11
賦值,我們寫成:
|
D3DXMATRIX M;
M(0, 0) = 5.0f;
// Set entry ij = 11 to 5.0f.
|
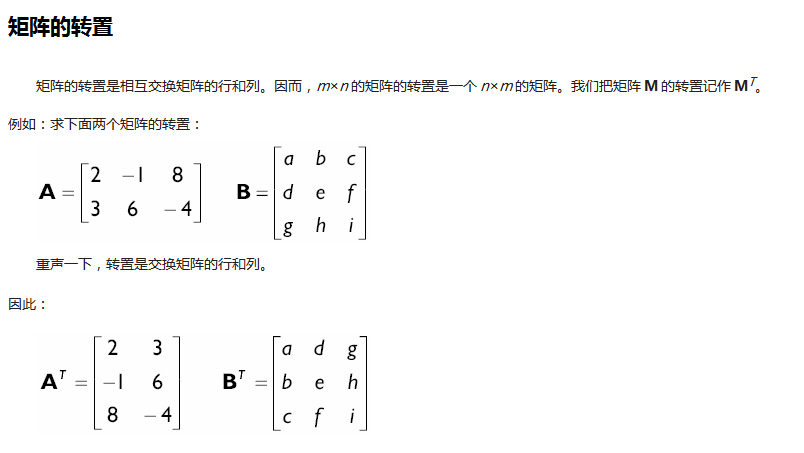
D3DX庫也提供下列有用的函數:將D3DXMATRIX轉化為單位矩陣,轉置D3DXMATRIX矩陣以及求逆矩陣。
D3DXMATRIX *D3DXMatrixIdentity(
D3DXMATRIX *pout
//
將矩陣轉換為單位矩陣
);
|
D3DXMATRIX M;
D3DXMatrixIdentity( &M );
// M =
單位矩陣
|
D3DXMATRIX *D3DXMatrixTranspose(
D3DXMATRIX *pOut,
//
輸出的轉置矩陣
CONST D3DXMATRIX *pM
//
原矩陣
);
|
D3DXMATRIX A(...);
//
初始化矩陣A
D3DXMATRIX B;
D3DXMatrixTranspose( &B, &A
); // B =
輸出的轉置矩陣
|
假如我們將不能求逆的矩陣用求逆函數,那么函數將會返回null.同樣的,這本書我們忽視第二個參數,并且總是把它設置為0。
D3DXMATRIX *D3DXMatrixInverse(
D3DXMATRIX *pOut,
//
輸出的逆矩陣
FLOAT *pDeterminant,
//
除非是必需的,一般設為0
CONST D3DXMATRIX *pM
//
原矩陣
);
|
D3DXMATRIX A(...);
//
初始化矩陣
D3DXMATRIX B;
D3DXMatrixInverse( &B, 0,
&A ); // B = A的逆矩陣
|