相交性測試的目的是檢測兩個幾何圖元是否相交,在某些情況下還要求出相交部分,這些基本測試構成了碰撞檢測系統的基礎。碰撞檢測用來防止物體互相穿越,或者使物體看起來好像互相被彈開。
我們將討論兩種不同類型的相交性測試:
(1)靜態測試檢測兩個靜止圖元是否相交。它是一種布爾型測試----也就是說,測試結果只有真(相交時)或假(不相交時)。如果兩個圖元相交,則可以獲取更多的信息。但一般來說,這種測試的目的只是返回一個布爾值。
(2)動態測試針對的是兩個運動圖元,檢測它們是否相交,及相交的時間點,運動值通常以參數形式來表達。因此,這種測試返回的結果不僅僅是一個布爾型的真/假值,還會返回一個指明相交時間點的值(參數t的值)。對于這里我們要討論的測試,運動值是一個簡單的線性位移---當t從0變化到1時原向量的偏移值。每個圖元都可以有自己的運動值,然而,從單個圖元的角度來考慮問題會比較簡單。也就是說,一個圖元被認為是靜止的,同時另一個圖元做了所有的運動。很容易做到這一點,只要將兩個位移向量組合成一個相對位移向量,它描述了兩個圖元間的相對移動關系。因此,所有動態測試總是涉及一個靜態圖元和一個動態圖元。
注意,包含射線在內的許多重要的測試實際上都是動態測試,因為射線能被看作一個運動的圖元。
在2D中兩條隱式直線的相交性檢測
在2D中,要檢測用隱式定義的兩條直線是否相交是非常簡單的,通過解線性方程組就能解決問題。
我們有兩個方程(兩條直線的隱式方程)和兩個未知數(交點的x、y坐標)。兩個方程分別為:
a1x + b1y = d1
a2x + b2y = d2
解此方程組得公式13.5:
x = (b2d1 - b1d2) / (a1b2
- a2b1)
y = (a1d2 - a2d1) / (a1b2
- a2b1)
公式13.5 計算2D中兩直線的交點
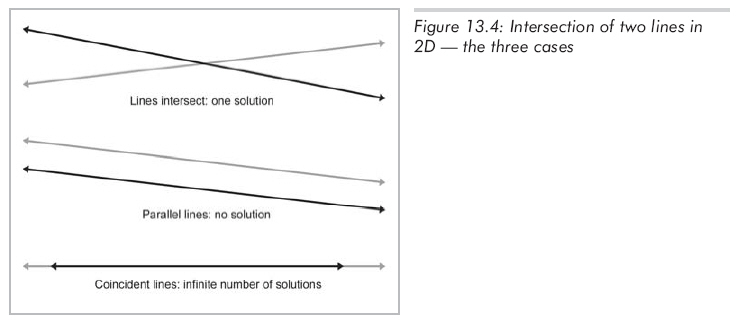
和其他方程組一樣,存在3中可能性(如圖13.4所示):
(1)只有一個解,這種情況下,公式13.5中的分母為非0值。
(2)無解,意味著直線是平行的,永遠不會相交,分母為0。
(3)無窮多解,意味著兩條直線重合,分母為0。
在3D中兩條射線的相交性檢測
考慮3D中兩條以參數形式定義的射線:
r1(t1) = p1 + t1d1
r2(t2) = p2 + t2d2
我們能夠解得它們的交點。暫時先不考慮t1、t2的取值范圍。因此我們考慮的是無限長的射線,同樣向量d1、d2也不必是單位向量。如果這兩條射線在一個平面中,那么也存在三種可能性:
(1)兩條射線交于一點。
(2)兩條射線平行,沒有交點。
(3)兩條射線重合,有無限多交點。
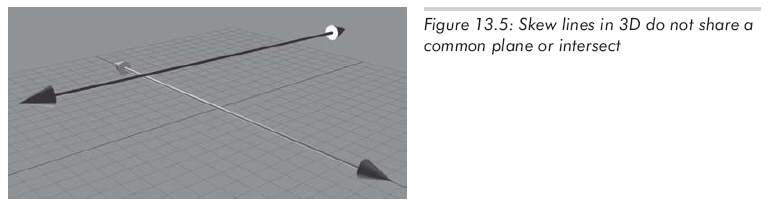
在3D中,還有第四種可能性,兩條射線不在一個平面中,如圖13.5所示:
下面演示如何解得交點處的t1、t2:

如果兩條射線平行或重合,d1、d2的叉乘為0,所以上面兩個等式的分母為0。如果兩條射線不在一個平面內,那么p1(t1)和p2(t2)是相距最近的點。通過檢查p1(t1)和p2(t2)間的距離即可確定兩條射線相交的情況。當然在實踐中因為浮點數的精度問題,精確的相交很少出現,這時就需要用到一個偏差值。
上面的討論假設沒有限定t1、t2的取值范圍,如果射線的長度有限(或只沿一個方向延伸),在計算出t1、t2后還應做適當的邊界檢測。
射線和平面的相交性檢測
在3D中射線與平面相交于一點,射線的參數定義為:
p(t) = p0 + td
平面以標準方式來定義,即對于平面上的所有點p,都滿足:
p . n = d
盡管n和d都被限制為單位向量,但這里是沒有必要加上這些限制條件的(如圖13.6):
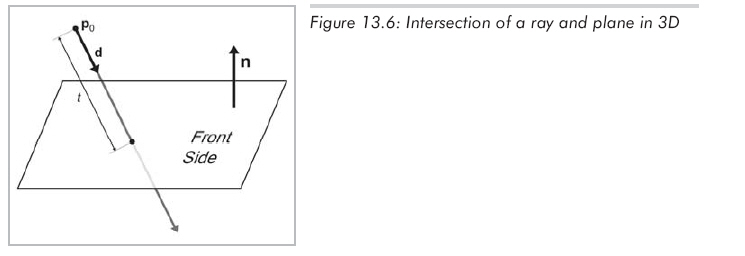
解得相交點的t值,暫時假設射線的長度是無限的(公式13.6):
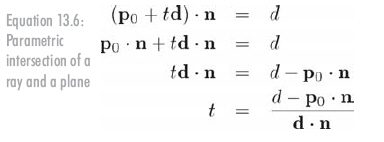
如果射線和平面互相平行,分母d . n
為0,則它們之間沒有交點。(我們僅討論與平面的正面相交的情況,在這種情況下,僅當射線的方向和平面的法向量相反時才有交點,此時d .
n < 0)。如果t超出了取值范圍,說明射線和平面不相交。