3D幾何圖元(7)
一般來說,多邊形是由頂點和邊構成的平面物體。
簡單多邊形與復雜多邊形
簡單多邊形不包含"洞",復雜多邊形可能包含"洞"(圖12.26)。簡單多邊形可以通過沿多邊形列出的所有頂點來描述(左手坐標系中,通常以從多邊形正面看時的順時針方向列出所有點)。簡單多邊形的使用頻率比復雜多邊形高得多。
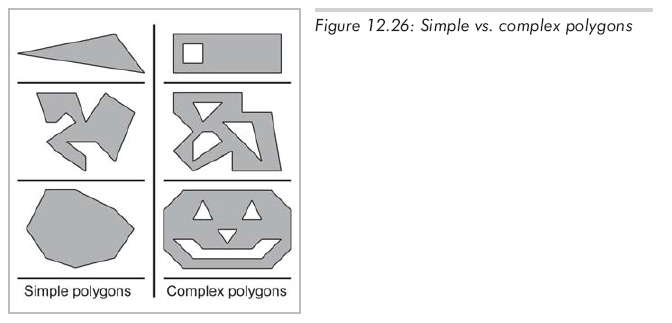
通過添加一對"接縫"邊,能將任意復雜多邊形轉化成簡單多邊形,如圖12.27所示。見右邊的放大圖,我們在每個"縫"添加了兩個邊,這兩個邊實際上是重合的,放大圖中將其分開是為了讓你看得更清楚。當我們考慮到繞多邊形的邊的順序時,這兩個接縫邊的方向是相反的。
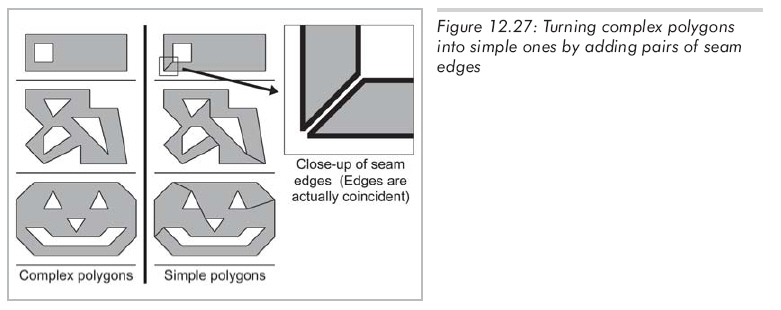
自相交多邊形
大多數簡單多邊形的邊不相交,如果有的邊相交了,那么這個多邊形叫做自相交多邊形。一個簡單的自相交多邊形如圖12.28所示。
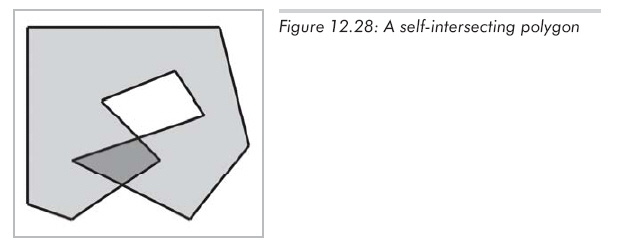
凸多邊形與凹多邊形
非自相交多邊形能進一步細分為凸多邊形和凹多邊形。給凸多邊形下一個精確定義是一件非常困難的事,因為存在很多令人棘手的退化形式。對大多數多邊形,下列常用的定義是等價的。不過對于一些退化多邊形來說,根據一種定義它是凸的,而根據另一種定義它又可能是凹的。
(1)直觀上,凸多邊形是沒有任何"凹陷處"的,而凹多邊形至少有一個頂點處于"凹陷處"----凹點。
(2)凸多邊形,任意兩頂點的連線都包含在多邊形中。但在凹多邊形中,總能找到一對頂點,它們的連線有一部分在多邊形外。
(3)沿凸多邊形周邊移動時,在每個頂點的轉向都是相同的。對凹多邊形,一些是向右轉,一些是向左轉,在凹點的轉向是相反的(注意這僅是對非自相交多邊形來說的)。
前面曾提到過,退化多邊形會使這些相對清晰的定義變得模糊不清。例如一些多邊形有兩個連續的頂點重合,或這一條邊以相反的方向重復了兩次。能認為這些多邊形是凸的嗎?實踐中,經常用到下列凸性的定義:
(1)如果只能對凸多邊形起作用的代碼對這個多邊形也能起作用,那么它就是凸的(也就是說如果一個定義沒有被打破就不用修正它)。
(2)如果凸性測試算法判斷它是凸的,那么它就是凸的(這是由"算法定義"解釋的)。
現在,讓我們忽略一些病態情況,給出一些大家意見都一致的凸、凹多邊形。如圖12.29所示,右上角的凹多邊形有1個凹點,而下面的凹多邊形有5個凹點。
任意凹多邊形都能分解為凸多邊形片,它的基本思路是定位凹點并通過添加對角線來有系統地移除它們。
怎樣才能知道一個多邊形是凸的還是凹的?一種方法是檢查各頂點的內角和,考慮n個頂點的凸多邊形,它的內角和為(n-2)180。,有兩種方法可以證明這個結論。
(1)設θi為頂點i的內角,很明顯,θi≤ 180。(假設多邊形是凸的)。在每個頂點上,補角為(180-θi)。,對于一個封閉的凸多邊形,全部頂點的補角之和為360。,有:
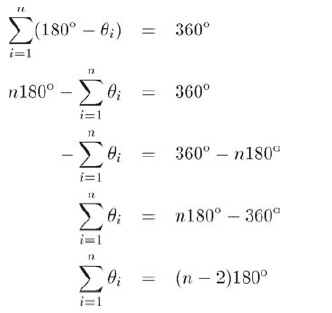
(2)任意n個頂點的凸多邊形都能分解為n-2個三角形,由經典幾何知識可知,三角形內角和為180。。所有三角形的內角和為(n-2)180。,可以看到,這個和總是等于多邊形的內角和。
不幸的是,凹多邊形和凸多邊形一樣,內角和也是(n-2)180。。怎樣才能進一步判斷一個多邊形是不是凸多邊形呢?對一個凸多邊形,內角不會大于外角。(外角不是補角,一對內角外角的和等于360。)
所以,將每個頂點處較小的角(內角或外角)相加,凸多邊形得到(n-2)180。,凹多邊形則小于它。怎樣判斷哪個角較小呢?幸運的是,有這樣一個工具 ---- 點乘,這種方法返回的角總是以較短的弧度來度量的。
下面的代碼說明了怎樣用角度和來判斷多邊形是否為凸多邊形。
// Function to determine if a polygon is convex. The polygon is
// assumed to be planar.
//
// Input:
// n Number of vertices
// vl pointer to array of of vertices
bool isConvex(int n, const Vector3 vl[])
{
// Initialize sum to 0 radians
float angleSum = 0.0f;
// Go around the polygon and sum the angle at each vertex
for (int i = 0 ; i < n ; ++i)
{
// Get edge vectors. We have to be careful on
// the first and last vertices. Also, note that
// this could be optimized considerably…
Vector3 e1;
if (i == 0)
e1 = vl[n–1] – vl[i];
else
e1 = vl[i–1] – vl[i];
Vector3 e2;
if (i == n–1)
e2 = vl[0] – vl[i];
else
e2 = vl[i+1] – vl[i];
// Normalize and compute dot product
e1.normalize();
e2.normalize();
float dot = e1 * e2;
// Compute smaller angle using “safe” function that protects
// against range errors which could be caused by numerical imprecision
float theta = safeAcos(dot);
// Sum it up
angleSum += theta;
}
// Figure out what the sum of the angles should be, assuming
// we are convex. Remember that pi/2 rad = 180 degrees
float convexAngleSum = (float)(n – 2) * kPiOverTwo;
// Now, check if the sum of the angles is less than it should be;
// then we’re concave. We give a slight tolerance for numerical imprecision
if (angleSum < convexAngleSum – (float)n * 0.0001f)
{
// We’re concave
return false;
}
// We’re convex, within tolerance
return true;
}
另一種檢測凸性的方法是檢測多邊形上是否有凹點,如果一個都沒有找到,就是凸多邊形。它的基本想法是每個頂點的轉向應該一致,任何轉向不一致的點都是凹點。
怎樣檢測一個點的轉向呢?技巧是利用邊向量的叉乘,左手坐標系中,如果向量的轉向是順指針,它們的叉乘就會指向你。什么是指向你呢?我們從多邊形的正面看,正面由法向量指明。如果沒有提供法向量,就必須做一些計算來得到。一旦有了法向量,檢查多邊形的每個頂點。用相鄰的兩個邊向量計算該頂點的法向量,接著用多邊形的法向量和頂點的法向量點乘,檢測它們的方向是否相反。如果是(點乘為負),那么這個頂點就是一個凹點。
三角分解和扇形分解
任意多邊形都能分解為三角形。因此,所有對三角形的操作都能應用到多邊形上。復雜、自相交、甚至簡單的凹多邊形的三角分解都不是一件簡單的工作。幸運的是,簡單多邊形的三角分解是一件容易的事。一種顯而易見的三角分解技術是選取一個點(稱作第一個點),沿著頂點按"扇形"分解多邊形。給定一個有n個頂點的多邊形,沿多邊形列頂點v1...vn,能夠很容易地構造形如{v1,vi-1, vi}的n-2個三角形,見圖12.30。
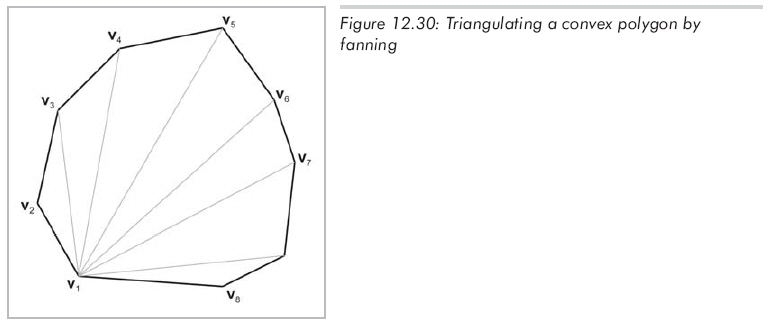
扇形三角分割會分割出一些長的、較細的三角形,這在某些情況下會引起麻煩。如同計算表面的法向量一樣,數值的不精確性在度量極小的角時會造成一些問題。
一種更加"聰明"的分解方法是:連接兩頂點的對角線將一個多邊形分解為兩部分。這時,對角線端點處的兩個內角都能分解為兩個新的內角。因此,總共產生了4個新內角。為了分解多邊形,選擇能使這4個新內角中最小的角最大化的對角線,用這條對角線將多邊形分為兩個。對分割后的每一部分都遞歸應用這個過程直到剩下的都是三角形。
這個方法產生較少的細三角形,但在實踐中,它過于復雜。根據幾何學和應用目的,扇形分解已經足夠了(并且簡單得多)。



