HTML clipboard
四元數記法
一個四元數包含一個標量和一個3D向量分量,經常記標量分量為w,記向量分量為單一的 v 或分開的x、y、z。兩種記法分別如下:
[w v ]
[w, (x, y, z)]
在某些情況下,用 v 這樣的短記法更方便,但在另一些情況下,"擴展"的記法會更清楚。
也可以將四元數豎著寫,有時這會使等式的格式一目了然,"行"或"列"四元數沒有明顯的區別。
四元數和復數
復數對(a, b)定義了數a+bi,i是所謂的虛數,滿足i2 = -1:a稱作實部,b稱作虛部。任意實數k都能表示為復數(k,
0)=k + 0i。
復數能夠相加、相減、相乘,如公式10.1所示:
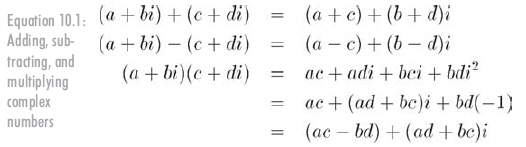
通過使虛部變負,還能夠計算復數的共軛,記法如公式10.2:
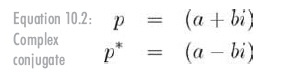
還能夠計算復數的模。這個運算的記法和解釋與實數的絕對值類似,實際上,如果將實數表示成復數,它們將產生相同的結果。公式10.3是計算復數大小的公式:
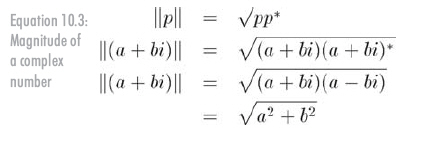
復數集存在于一個2D平面上,可以認為這個平面有兩個軸:實軸和虛軸。這樣,就能將復數(x,
y)解釋為2D向量。用這種方法解釋復數時,它們能用來表達平面中的旋轉。看看復數p繞原點旋轉角度θ的情況,如圖10.9所示:
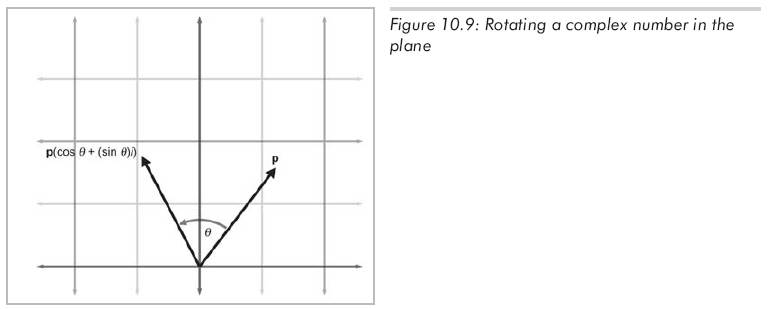
為進行這個旋轉,引入第二個復數 q = (cosθ, sinθ)。現在,旋轉后的復數p'能用復數乘法計算出來:
p = x + yi
q = cosθ + i sinθ
p' = pq = (x + yi)(cosθ + i sinθ) = (xcosθ - ysinθ) + (xsinθ + ycosθ)i
引入復數q和用2x2旋轉矩陣達到的效果是一樣的,但復數提供了另一種有趣的記法。
四元數擴展了復數系統,它使用三個虛部i, j, k。它們的關系如下:
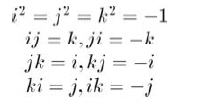
一個四元數[w, (x, y, z)]定義了復數
w+xi+yj+zk,很多標準復數的性質都能應用到四元數上。更重要的是,和復數能用來旋轉2D中的向量類似,四元數也能用來旋轉3D中的向量。
四元數和軸-角對
歐拉證明了一個旋轉序列等價于單個旋轉。因此,3D中的任意角位移都能表示為繞單一軸的單一旋轉(這里的軸是一般意義上的旋轉軸,不要和笛卡爾坐標軸混淆。顯然,旋轉軸的方向是任意的)。當一個方位用這種形式來描述時稱作軸-角描述法(實際上,能將軸-角形式作為描述方位的第四種表達方式。但是,軸-角對很少用到,經常被歐拉角或四元數替代)。
設 n 為旋轉軸,對于旋轉軸來說長度并不重要,將 n 定義為單位長度會比較方便。根據左手或右手法則, n 的方向定義了哪邊將被認為是旋轉"正"方向。設θ為繞軸旋轉的量,因此,軸-角對( n ,
θ)定義了一個角位移:繞 n 指定的軸旋轉θ角。
四元數能被解釋為角位移的軸-角對方式。然而, n 和θ不是直接存儲在四元數的四個數中,它們的確在四元數里,但不是那么直接。公式10.4列出了四元數中的數和 n ,θ的關系,兩種四元數加法都被使用了。
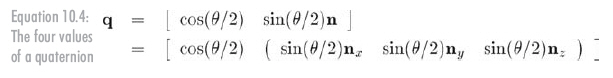
記住, q 的w分量和θ有關系,但它們不是一回事。同樣, v 和 n 也有關系但不完全相同。
負四元數
四元數能求負,做法很直接,將每個分量對變負,見公式10.5:
- q = -[w (x y z)] = [-w (-x -y -z)] = -[w v ]
= [-w - v ]
公式10.5 四元數求負
q 和- q 代表的實際角位移是相同的,很奇怪吧!如果我們將θ加上360度的倍數,不會改變 q 代表的角位移,但它使 q 的四個分量都變負了。因此,3D中的任意角位移都有兩種不同的四元數表示方法,它們互相為負。
單位四元數
幾何上,存在兩個"單位"四元數,它們代表沒有角位移,[1, 0 ]和[-1, 0 ](注意粗體 0 ,它們代表零向量)。當θ是360度的偶數倍時,有第一種形式,cos(θ/2)=1;θ是360度的奇數倍時,cos( θ /2)=-1。在兩種情況下,都有sin(θ/2)=0,所以 n 的值無關緊要。它的意義在于:
當旋轉角θ是360度的整數倍時,方位并沒有改變,并且旋轉軸也是無關緊要的。
數學上,實際只有一個單位四元數:[1, 0 ]。用任意四元數 q 乘以單位四元數[1,
0 ],結果仍是 q 。任意四元數 q 乘以另一個"幾何單位"[-1,
0 ]時得到- q 。幾何上,因為 q 和- q 代表的角位移相同,可認為結果是相同的。但在數學上, q 和- q 不相等,所以[-1,
0 ]并不是"真正"的單位四元數。
四元數的模
和復數一樣,四元數也有模。記法和公式都和向量類似,如公式10.6所示:
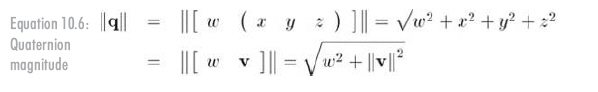
讓我們看看它的幾何意義,代入 θ 和 n ,可得到:
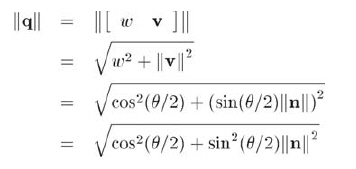
n 為單位向量,所以:
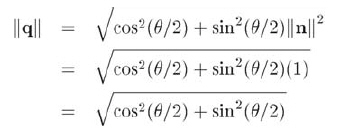
應用三角公式sin2x + cos2x = 1,得到:
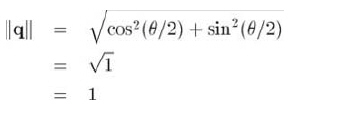
如果為了用四元數來表示方位,我們僅使用符合這個規則的單位四元數。
四元數共軛和逆
四元數的共軛記作 q *,可通過讓四元數的向量部分變負來獲得,見公式10.7:
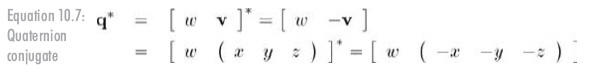
四元數的逆記作 q ^-1,定義為四元數的共軛除以它的模,見公式10.8:
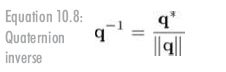
四元數的逆和實數的倒數有著有趣的對應關系。對于實數a,它的逆a-1為1/a,從另一方面說,aa-1 = a-1a
= 1。四元數的逆也有著同樣的性質,一個四元數 q 乘以它的逆 q -1,即可得到單位四元數[1,
0 ]。
公式10.8是四元數逆的正式定義,但我們只使用單位四元數,所以四元數的逆和共軛是相等的。
共軛非常有趣,因為 q 和 q *代表相反的角位移。很容易驗證這種說法,使 v 變負,也就是使旋轉軸反向,它顛倒了我們所認為的旋轉正方向。因此, q 繞軸旋轉θ角,而 q *沿相反的方向旋轉相同的角度。