《編程之美》讀書筆記13： 4.1 金剛坐飛機問題
問題：
現(xiàn)在有一班飛機將要起飛，乘客們正準備按機票號碼（1, 2, 3, …N）依次排隊登機。突然來了一只大猩猩（對，他叫金剛）。他也有飛機票，但是他插隊第一個登上了飛機，然后隨意地選了一個座位坐下了1。根據(jù)社會的和諧程度，其他的乘客有兩種反應：
1. 乘客們都義憤填膺，“既然金剛同志不遵守規(guī)定，為什么我要遵守？”他們也隨意地找位置坐下，并且堅決不讓座給其他乘客。
2. 乘客們雖然感到憤怒，但還是以“和諧”為重，如果自己的位置沒有被占領，就趕緊坐下，如果自己的位置已經(jīng)被別人（或者金剛同志）占了，就隨機地選擇另一個位置坐下，并開始閉目養(yǎng)神，不再挪動位置。
那么，在這兩種情況下，第 i 個乘客（除去金剛同志之外）坐到自己原機票位置的概率分別是多少？
對問題一，每個人都是隨機選擇座位，任意一個人坐在指定座位的概率相同，因而第i個乘客坐在其座位的概率是 1/n。
對問題二，答案和金剛的原來座位編號有關。不妨先去除金剛的座位，將乘客（根據(jù)機票號）和剩下的座位，按原大小順序從1開始重新編號。用F(i，n)表示在新排列中（共有n-1個乘客座位和金剛原來的座位），新的第i個乘客坐在其原來座位的概率，則在n個座位中：
① 金剛若挑自己的座位或選的座位在第i個座位后（共有n-i個座位滿足這個條件），則第i個乘客肯定能坐到原來的座位；
② 金剛若挑選的座位在第i個座位前，不妨假設為j，則第j個乘客除非坐到金剛的座位，不然就會搶其他人的座位，因為他的行為和金剛相似，可以將他當做金剛處理。去除前j個座位，剩下的座位和乘客再按原大小排序重新從1開始編號，則先前的第i個乘客，其座位號變?yōu)?span lang=EN-US>i-j，新的總座位數(shù)變?yōu)?span lang=EN-US>n-j。因而可得公式：
用 G(i, n)表示原排列中，第i個乘客坐到自己座位的概率，假設金剛的座位編號為j。
若 i<j 則 G(i,n)=F(i,n)= (n-i)/(n+1-i)。
若 i>j 則 G(i,n)=F(i-1,n)= (n+1-i)/(n+2-i) 。
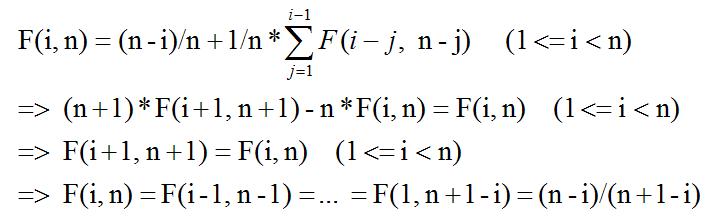
類似題：
“約瑟芬環(huán)：n個人，編號為0到n-1，圍成一圈，從編號為0的開始，從1開始報數(shù)，所有報到m的出列，下一個人從1開始繼續(xù)報數(shù)。求最后一個人的編號。”