pdf版本下載㈠ Fibonacci數(shù)
剛接觸Fibonacci數(shù)的時(shí)候,在網(wǎng)上看到“矩陣法”,看到要先實(shí)現(xiàn)一個(gè)矩陣乘法,感覺(jué)太麻煩了。后來(lái)仔細(xì)觀察Fibonacci數(shù)列,發(fā)現(xiàn)有下面的規(guī)律:
F(n) = F(k)*F(n+1-k) + F(k-1)*F(n-k) =>
F(2*n) = F(n+1) * F(n) + F(n) * F(n - 1)
F(2*n+1) = F(n+1) * F(n+1) + F(n) * F(n)
根據(jù)該公式:要計(jì)算F(n),只需先計(jì)算出F(n/2)和F(n/2+1),于是得出一個(gè)數(shù)的O(log n)解法。(例如:計(jì)算F(13) => 計(jì)算F(6)、F(7) => 計(jì)算F(3)、F(4) => 計(jì)算F(1)、F(2)。)
再后來(lái)無(wú)意間發(fā)現(xiàn),“矩陣法”根本就不必實(shí)現(xiàn)一個(gè)矩陣,網(wǎng)上廣為流傳的糟糕的做法,掩蓋了“矩陣法”的優(yōu)美。
先回顧下Fibonacci數(shù)列的矩陣法:
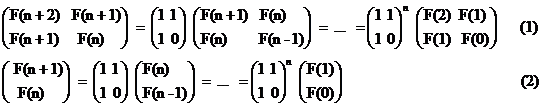
上式中,對(duì)系數(shù)矩陣A求n次方,有O(log n)解法,因而整個(gè)算法是O(log n)。
某些介紹矩陣法的文章,會(huì)“偷懶”采用上面的第二種寫(xiě)法,而不是第一種寫(xiě)法。偷懶的結(jié)果,總是要付出代價(jià)的。對(duì)上面矩陣法的實(shí)現(xiàn),存在兩個(gè)盲點(diǎn),也正由于這兩個(gè)盲點(diǎn),使“矩陣法”的實(shí)現(xiàn)代碼看起來(lái)很復(fù)雜,失去了簡(jiǎn)潔之美。
盲點(diǎn)之一:對(duì)系數(shù)矩陣A求n次方,可以不采用矩陣乘法來(lái)實(shí)現(xiàn)。
將F(1) = F(2) = 1, F(0) = 0代入上面的公式1,得到:
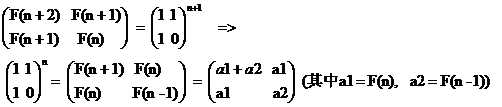
上式,對(duì)任意 n >=1都成立,也就是說(shuō)A的任意n次方,只要用兩個(gè)變量表示,根本沒(méi)必要去實(shí)現(xiàn)矩陣乘法。
另外,由 A^n = A^k * A^(n-k),結(jié)合上式,很容易就得到前面提到的公式:
F(n) = F(k)*F(n+1-k) + F(k-1)*F(n-k),
盲點(diǎn)之二: A的n次方計(jì)算方法。
計(jì)算一個(gè)數(shù)m的n次方,
若采用迭代法的話,一般是將m^n,拆分成m、m^2、m^4、m^8…中的幾個(gè)的乘積。
若采用遞歸的話,則是將m^n拆分成計(jì)算m^(n/2)
//迭代法:
int pow1(int m, unsigned n)
{
int result = 1;
int factor = m;
while (n) {
if (n & 1) { result *= factor; }
factor *= factor;
n /= 2u;
}
return result;
}
//遞歸法
int pow2(int m, unsigned n)
{
if (n == 0) return 1;
int square_root = pow2(m, n / 2);
int result = square_root * square_root;
if (n & 1) result *= m;
return result;
}
對(duì)于計(jì)算一個(gè)整數(shù)的n次方,顯然第一種解法效率高,但對(duì)計(jì)算矩陣的n次方,第二種解法(遞歸法)則更簡(jiǎn)單。該遞歸算法也可寫(xiě)成迭代形式:
int pow3(int m, unsigned n)
{
if (n == 0) return 1;
unsigned flag = n; //小等于n的最大的2的k次冪
for (unsigned value = n; value &= (value - 1); ) flag = value;
int result = m;
while (flag >>= 1) {
result *= result;
if (n & flag) result *= m;
}
return result;
}
(求小等于n的最大的2的k次冪(或求二進(jìn)制表示中的最高/左位1),有兩種不通用的O(1)方法:一種是使用位掃描匯編指令、另外一種是利用浮點(diǎn)數(shù)的二進(jìn)制表示。)
unsigned extract_leftmost_one(unsigned num)
{
union {
unsigned i;
float f;
} u;
u.f = (float)num;
return u.i >> 23;
}
最后可得到如下代碼:
① 采用一般迭代法計(jì)算A^n
static inline void matrix_multiply(uint& b1, uint& b2, uint a1, uint a2)
{
const uint r1 = a1 * b1 + a1 * b2 + a2 * b1;
const uint r2 = a1 * b1 + a2 * b2;
b1 = r1;
b2 = r2;
}
uint fib_matrix(uint num)
{
uint b1 = 0, b2 = 1;
uint a1 = 1, a2 = 0;
for (; num != 0; num >>= 1) {
if (num & 1) matrix_multiply(b1, b2, a1, a2);
matrix_multiply(a1, a2, a1, a2);
}
return b1;
}
② 采用新的迭代法計(jì)算A^n
typedef unsigned uint;
uint fibonacci(uint num)
{
if (num == 0) return 0;
uint flag = num; //extract_leftmost_one
for (uint value = num; value &= value - 1; ) flag = value;
uint a1 = 1, a2 = 0;
while (flag >>= 1) {
const uint r1 = a1 * a1 + 2 * a1 * a2;
const uint r2 = a1 * a1 + a2 * a2;
a1 = r1;
a2 = r2;
if (num & flag) {
a1 = r1 + r2;
a2 = r1;
}
}
return a1;
}
上面提到的方法,很容易擴(kuò)展到三階矩陣,下面是《編程之美》書(shū)上的一道擴(kuò)展題的解法:
(具體分析見(jiàn)下一節(jié))
假設(shè):A(0)=1, A(1)=2, A(2)=2,對(duì)n>2都有A(n)=A(n-1)+A(n-2)+A(n-3),
1. 對(duì)于任何一個(gè)給定的n,如何計(jì)算出A(n)?
2. 對(duì)于n非常大的情況,如n=2^60的時(shí)候,如何計(jì)算A(n) mod M (M < 100000)呢?
typedef unsigned uint;
typedef unsigned long long uint64;
uint fib_ex(uint64 num, uint M)
{
assert(M != 0);
const uint g0 = 1, g1 = 2, g2 = 2;
if (num == 0) return g0;
uint64 flag = num;
for (uint64 value = num; value &= value - 1; ) flag = value;
uint64 a1 = 0, a2 = 1, a3 = 0;
while (flag >>= 1) {
const uint64 r1 = 2 * (a1 + a2 + a3) * a1 + a2 * a2;
const uint64 r2 = 2 * (a1 + a2) * a1 + 2 * a2 * a3;
const uint64 r3 = (a1 + 2 * a2) * a1 + a3 * a3;
a1 = r1;
a2 = r2;
a3 = r3;
if (num & flag) {
a1 = r1 + r2;
a2 = r1 + r3;
a3 = r1;
}
a1 %= M;
a2 %= M;
a3 %= M;
}
return (a1 * g2 + a2 * g1 + a3 * g0) % M;
}
㈡ 擴(kuò)展數(shù)列的通解:
下面將前面的結(jié)果擴(kuò)展到任意m階數(shù)列:

例子:
① m=2: g(n) = f1 * g(n-1) + f2 * g(n-2), 初始值為:g0 = g(0), g1=g(1)
設(shè)系數(shù)矩陣為A,An的最后一行為(a1 a2),則
倒數(shù)第二行為:(f1*a1 + a2 f2*a1)
即:
系數(shù)矩陣A An
f1 f2 f1*a1 + a2 f2*a1
1 0 a1 a2
typedef unsigned uint;
uint fib_matrix2(uint num)
{
if (num == 0) return g0;
uint flag = num;
for (uint value = num; value &= value - 1; ) flag = value;
/*
A A^n
f1 f2 f1*a1 + a2 f2*a1
1 0 a1 a2
*/
uint a1 = 1, a2 = 0; // 0 0 ... 1 0
while (flag >>= 1) {
const uint r1 = f1 * a1 * a1 + 2 * a1 * a2;
const uint r2 = f2 * a1 * a1 + a2 * a2;
a1 = r1;
a2 = r2;
if (num & flag) {
a1 = f1 * r1 + r2;
a2 = f2 * r1;
}
}
return a1 * g1 + a2 * g0;
}
② m=3: g(n) = f1 * g(n-1) + f2 * g(n-2) + f3*g(n-3),初始值為:g0 = g(0),g1=g(1), g2=g(2)
設(shè)系數(shù)矩陣為A,An的最后一行為(a1 a2 a3),則
倒數(shù)第二行為:(f1*a1 + a2 f2*a1 + a3 f3*a1)
倒數(shù)第三行為:((f1*f1+f2)*a1 + f1*a2 + a3 (f1*f2+f3)*a1 + f2*a2 f1*f3*a1 + f3*a2)
即:
系數(shù)矩陣A An
f1 f2 f3 (f1*f1+f2)*a1 + f1*a2 + a3 (f1*f2+f3)*a1 + f2*a2 f1*f3*a1 + f3*a2
1 0 0 f1*a1 + a2 f2*a1 + a3 f3*a1
0 1 0 a1 a2 a3
typedef unsigned uint;
uint fib_matrix3(uint num)
{
if (num == 0) return g0;
uint flag = num;
for (uint value = num; value &= value - 1; ) flag = value;
/*
A A^n
f1 f2 f3 (f1*f1+f2)*a1 + f1*a2 + a3 (f1*f2+f3)*a1 + f2*a2 f1*f3*a1 + f3*a2
1 0 0 f1*a1 + a2 f2*a1 + a3 f3*a1
0 1 0 a1 a2 a3
*/
uint a1 = 0, a2 = 1, a3 = 0; // 0 0 ... 1 0
while (flag >>= 1) {
const uint r1 = (f1 * f1 + f2) * a1 * a1 + 2 * f1 * a1 * a2 + 2 * a1 * a3 + a2 * a2;
const uint r2 = (f1 * f2 + f3) * a1 * a1 + 2 * f2 * a1 * a2 + 2 * a2 * a3;
const uint r3 = (f1 * f3) * a1 * a1 + 2 * f3 * a1 * a2 + a3 * a3;
a1 = r1;
a2 = r2;
a3 = r3;
if (num & flag) {
a1 = f1 * r1 + r2;
a2 = f2 * r1 + r3;
a3 = f3 * r1;
}
}
return a1 * g2 + a2 * g1 + a3 * g0;
}