轉(zhuǎn)自：http://www.shnenglu.com/lovedday/archive/2008/05/02/48628.html

世界變換

世界變換就是將物體頂點坐標從模型空間轉(zhuǎn)換到世界空間。在模型空間里，頂點位置坐標依據(jù)模型的本地坐標系的原點而定，在世界空間里，所有模型的頂點共用一個原點，即世界坐標系原點。事實上，世界變換就是將一個模型從本地空間重新定位到世界空間內(nèi)。從模型空間到世界空間的轉(zhuǎn)換實際上就是對模型進行平移、旋轉(zhuǎn)、縮放以及它們的任意組合變換。

使用三維模型制作軟件，例如3dmax，制作三維模型時，首先需要為模型設(shè)定一個坐標系，模型上的頂點坐標就是設(shè)定的模型自身坐標系下的坐標，這個坐標系也就是上面提到的本地坐標系或模型空間。

 

1、世界變換矩陣

在處理三維圖像的應(yīng)用程序中，可使用世界變換完成一個物體（確切的說是一個坐標或一系列坐標）的平移、旋轉(zhuǎn)和縮放。當(dāng)然也可以完成這三種變換的任意組合。具體的方法就是通過下式：

將任意一點P(x, y, z)轉(zhuǎn)換到p'(x', y', z')，上式也可以表示為以下形式：

p'(x', y', z') = P(x, y, z) . M_world

M_world就是世界變換矩陣。也就是它實現(xiàn)了物體的平移、旋轉(zhuǎn)、縮放和它們的復(fù)合變換。在定義好世界變換矩陣后，調(diào)用函數(shù)IDirect3DDevice9::SetTransform()并指定第一個參數(shù)為D3DTS_WORLD，第二個參數(shù)為相應(yīng)的世界變換矩陣即可。

 

2、平移

可以通過下式（也就是下面的平移變換矩陣）：

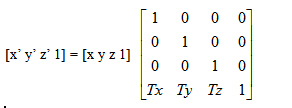
將點（x, y, z）沿x、y和z軸分別移動T_x、T_y、T_z，到另一點（x'，y'，z'）。很顯然，只要得到了這個平移矩陣，平移工作就可以完成。

為方便起見，D3DX擴展函數(shù)庫d3dx9.lib提供了函數(shù)D3DXMatrixTranslation()，用它可以很方便地生成一個平移世界矩陣。該函數(shù)的聲明如下:

Builds a matrix using the specified offsets.

D3DXMATRIX * D3DXMatrixTranslation(
  D3DXMATRIX * pOut,
  FLOAT x,
  FLOAT y,
  FLOAT z
);

Parameters

pOut

[in, out] Pointer to the D3DXMATRIX structure that is the result of the operation.

x

[in] X-coordinate offset.

y

[in] Y-coordinate offset.

z

[in] Z-coordinate offset.

Return Values

Pointer to a D3DXMATRIX structure that contains a translated transformation matrix.

Remarks

The return value for this function is the same value returned in the pOut parameter. In this way, the D3DXMATRIXTranslation can be used as a parameter for another function.

 

3、旋轉(zhuǎn)

與平移類似，使用下面的四階矩陣可以將點（x, y, z）繞x軸旋轉(zhuǎn)θ角，到新點（x', y', z'）:

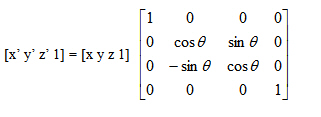
繞y軸旋轉(zhuǎn)θ角時的矩陣為：

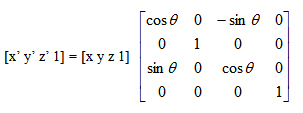
繞z軸旋轉(zhuǎn)θ角時的矩陣為：

θ指旋轉(zhuǎn)角度，單位是弧度，具體是指沿著旋轉(zhuǎn)軸的指向（即正方向）向坐標原點看去順指針旋轉(zhuǎn)過的角度。

同樣可以使用D3DX擴展函數(shù)庫d3dx9.lib提供的函數(shù)D3DXMatrixRotationX()、D3DXMatrixRotationY()和D3DXMatrixRotationZ()方便地創(chuàng)建旋轉(zhuǎn)矩陣，這三個函數(shù)的聲明如下，因聲明類似，只列出D3DXMatrixRotationX()的使用說明:

Builds a matrix that rotates around the x-axis.

D3DXMATRIX * D3DXMatrixRotationX(
  D3DXMATRIX * pOut,
  FLOAT Angle
);

Parameters

pOut

[in, out] Pointer to the D3DXMATRIX structure that is the result of the operation.

Angle

[in] Angle of rotation in radians. Angles are measured clockwise when looking along the rotation axis toward the origin.

Return Values

Pointer to a D3DXMATRIX structure rotated around the x-axis.

Remarks

The return value for this function is the same value returned in the pOut parameter. In this way, the D3DXMatrixRotationX function can be used as a parameter for another function.

 

4、縮放

使用下面的四階矩陣可以將點（x, y, z）在x、y、z軸上各縮放Sx、Sy、Sz，到另一點（x', y', z'）。

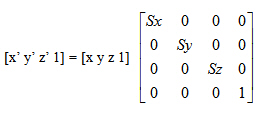
同樣，可以使用Direct3D擴展實用庫中的函數(shù)D3DXMatrixScaling()來生成縮放矩陣，該函數(shù)的聲明如下：

Builds a matrix that scales along the x-axis, the y-axis, and the z-axis.

D3DXMATRIX * D3DXMatrixScaling(
  D3DXMATRIX * pOut,
  FLOAT sx,
  FLOAT sy,
  FLOAT sz
);

Parameters

pOut

[in, out] Pointer to the D3DXMATRIX structure that is the result of the operation.

sx

[in] Scaling factor that is applied along the x-axis.

sy

[in] Scaling factor that is applied along the y-axis.

sz

[in] Scaling factor that is applied along the z-axis.

Return Values

Pointer to the scaling transformation D3DXMATRIX.

Remarks

The return value for this function is the same value returned in the pOut parameter. In this way, the D3DXMatrixScaling function can be used as a parameter for another function.

 

5、矩陣連接與復(fù)合變換

在大多數(shù)情況下，Direct3D中的物體需要進行的世界變換不止一個，而往往是多個世界變換的組合，這時可以使用矩陣連接來實現(xiàn)這種復(fù)合變換。因為矩陣的一個優(yōu)點是通過矩陣的相乘，將兩個或更多矩陣的作用合并在一起實現(xiàn)。為了先后實現(xiàn)一個模型的旋轉(zhuǎn)和移動，不需要使用兩個矩陣，可以將旋轉(zhuǎn)矩陣和平移矩陣相乘得到一個復(fù)合矩陣以實現(xiàn)所有功能。這個過程叫做矩陣連接（matrix concatention），可以用下面的公式表示：

C = M₁ * M₂ * ... * M_n-1 * M_n

在這個公式里，C是實現(xiàn)復(fù)合變換的復(fù)合矩陣，從M₁到M_n是只能實現(xiàn)某一種世界變換的單獨矩陣（individual matrices）。大多數(shù)情況下是兩到三個矩陣連接，但這個數(shù)量沒有限制。

使用函數(shù)D3DXMatrixMultiply() 可完成矩陣的乘法，該函數(shù)的說明如下：

Determines the product of two matrices.

D3DXMATRIX * D3DXMatrixMultiply(
  D3DXMATRIX * pOut,
  CONST D3DXMATRIX * pM1,
  CONST D3DXMATRIX * pM2
);

Parameters

pOut

[in, out] Pointer to the D3DXMATRIX structure that is the result of the operation.

pM1

[in] Pointer to a source D3DXMATRIX structure.

pM2

[in] Pointer to a source D3DXMATRIX structure.

Return Values

Pointer to a D3DXMATRIX structure that is the product of two matrices.

Remarks

The result represents the transformation M1 followed by the transformation M2 (Out = M1 * M2).

The return value for this function is the same value returned in the pOut parameter. In this way, the D3DXMatrixMultiply function can be used as a parameter for another function.

矩陣pOut表示最終的復(fù)合變換，也就是先進行矩陣pM1表示的變換，然后又進行矩陣pM2表示的變換。

在矩陣的乘法中，順序是很關(guān)鍵的。無論要創(chuàng)建什么樣的世界變換矩陣，記住從左到右的原則才能確保實現(xiàn)想要的效果，也就是說，一個復(fù)合矩陣的視覺效果是按從左到右的順序各單獨矩陣視覺效果的組合。假設(shè)一個物體先繞y軸旋轉(zhuǎn)，然后把它移動到場景內(nèi)的另一個位置。為實現(xiàn)這個效果，首先創(chuàng)建一個旋轉(zhuǎn)矩陣R_y，然后乘以一個平移矩陣T_w：

W = R_y * T_w

在這個公式里，R_y表示繞y軸的旋轉(zhuǎn)矩陣，T_w實現(xiàn)世界坐標系內(nèi)的一次平移。矩陣的乘法不滿足交換律。如果將這兩個矩陣以相反的順序相乘，效果是先平移，然后旋轉(zhuǎn)。