暑假了，打算寫一個3D游戲引擎。
其實(shí)也就是把一些類封裝一下，讓開發(fā)更簡結(jié)，以開源和實(shí)用為第一準(zhǔn)則。
最近看了本好書--《3D計(jì)算機(jī)圖形學(xué)》，真的太精彩了。
雖然是基于OpenGL的，而我更喜歡DirectX3D，但這畢竟是次要的。
它每一點(diǎn)知識都將地很深入，建議大家有時間看一看。
目錄：
第1章 引言
第2章 變換與觀察
第3章 光照、亮度和著色
第4章 均值與插值
第5章 紋理映射
第6章 彩色
第7章 貝塞爾曲線
第8章 B樣條曲線
第9章 光線跟蹤
第10章 相交測試
第11章 輻射度
第12章 動畫與運(yùn)動學(xué)
附錄A 數(shù)學(xué)背景知識
A.1 預(yù)備知識
A.2 向量和向量積
A.2.1 R2中的向量
A.2.2 R3中的向量
A.3 矩陣
A.3.1 R3中矩陣和向量的積
A.3.2 行列式，逆矩陣和伴隨矩陣
A.3.3 線性子空間
A.4 多元微積分
A.4.1 多元函數(shù)
A.4.2 向量值函數(shù)
A.4.3 多元向量值函數(shù)
附錄B 光線跟蹤軟件包
B.1 介紹
B.2 高層光線跟蹤函數(shù)
B.3 光線跟蹤API
B.3.1 指定光源
B.3.2 定義相機(jī)和視窗
B.3.3 按像素陣列工作
B.3.4 定義材質(zhì)
B.3.5 定義可見物體
B.3.6 可見的球
B.3.7 可視的三角形和平行四邊形
B.3.8 可見的橢球
B.3.9 可視的圓柱體
B.3.10 可視的錐體
B.3.11 可視的平行六面體
B.3.12 可視的圓環(huán)
B.3.13 可視的貝塞爾面片
B.3.14 紋理映射
索引
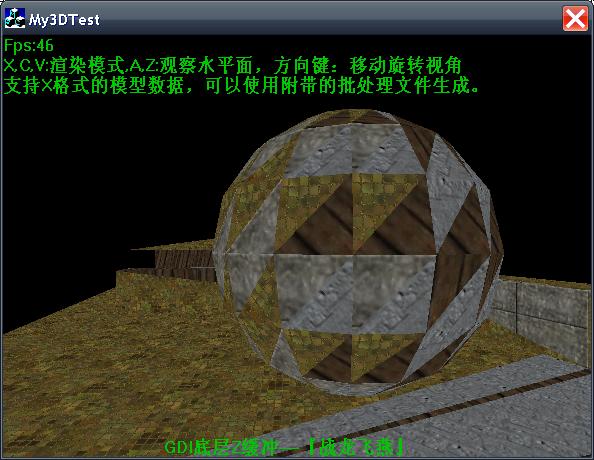
在CSDN上看到了一個很強(qiáng)大的程序：用GDI實(shí)現(xiàn)3D,可以變換視角的查看.x文件。
不過想想看，好像實(shí)現(xiàn)起來也并不難。。。
和所有基礎(chǔ)的3D程序一樣，先把視椎變換為單位立方體，
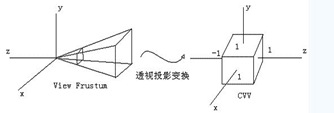
變換矩陣為：
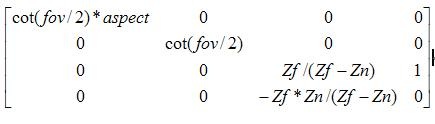
當(dāng)然，DirectX和OpenGL里都有現(xiàn)成的函數(shù)：
//OpenGL
void?gluPerspective(GLdouble?fovy,
????GLdouble?aspect,
????GLdouble?zNear,
????GLdouble?zFar);
//DirectX
D3DXMatrixPerspectiveFovLH(?D3DXMATRIX?*pOut,
????FLOAT?fovY,
????FLOAT?Aspect,
????FLOAT?zn,
????FLOAT?zf
);?
單位立方體中的點(diǎn)正交投影得到的(x,y,z)*視口變換矩陣 得到 (x',y',z')。
(x',y')對應(yīng)屏幕點(diǎn)，z'為其深度，用于點(diǎn)的競爭。
把每個三角面匹配紋理用GDI基本函數(shù)畫出來就可以了。
CSDN的那個程序
寫作業(yè)時，寫到了2007年高考2卷 理綜物理第25題，解第二小問時，得到一個平方為負(fù)數(shù)的奇怪式子，
感到很神奇，于是baidu了一下。很多人都說這題錯了。。
如圖所示，在坐標(biāo)系Oxy的第一象限中存在沿y軸正方形的勻強(qiáng)電場，場強(qiáng)大小為E。在其它象限中存在勻強(qiáng)磁場，磁場方向垂直于紙面向里。A是y軸上的一點(diǎn)，它到座標(biāo)原點(diǎn)O的距離為h；C是x軸上的一點(diǎn)，到O點(diǎn)的距離為l，一質(zhì)量為m、電荷量為q的帶負(fù)電的粒子以某一初速度沿x軸方向從A點(diǎn)進(jìn)入電場區(qū)域，繼而通過C點(diǎn)進(jìn)入大磁場區(qū)域，并再次通過A點(diǎn)。此時速度方向與y軸正方向成銳角。不計(jì)重力作用。試求：
（1）粒子經(jīng)過C點(diǎn)時速度的大小合方向；
（2）磁感應(yīng)強(qiáng)度的大小B。
設(shè) 圓心到y(tǒng)軸距離為b,到x軸距離為a。然后就可以得到h*h=-bl這樣神奇的結(jié)果。。。
如果"速度方向與y軸正方向成鈍角"，才可以得到答案
不禁想起“三聚氰胺”毒奶粉事件，全國那么多磚家一起發(fā)功，還是會出這樣的問題。。。