??? kD 樹是二叉樹結(jié)構(gòu)的一個(gè)變種，當(dāng)前主要用于加速光纖跟蹤的遍歷過程。最簡單的排序二叉樹以各個(gè)元素的大小關(guān)系作為分割點(diǎn)，而 kD 樹簡而言之就是從數(shù)據(jù)中選擇一個(gè)“維度”構(gòu)造一個(gè)超平面對數(shù)據(jù)集進(jìn)行分割。比如要對學(xué)生數(shù)據(jù)進(jìn)行分割，找出哪些學(xué)生的生日小于 2 月 18 日，那么就只要遍歷整個(gè)集合，把所有的數(shù)據(jù)分成。如果又要在符合第一次條件的學(xué)生中找出哪些學(xué)生是來自南京的，那么就只要再次進(jìn)行比較規(guī)劃就可以辦到了。 kD 樹的帶來的性能提升很高，讓我們看一下常用加速結(jié)構(gòu)的復(fù)雜度 [1] ，從 O(N) 到 O(logN) ：

Bounding Volumn Hierarchy
Grid
Octree （包括 Quadtree ）
kD Tree

　　一般來說，構(gòu)造 kD 樹的方式有兩種：排序和掃描。我們參考了一些加速構(gòu)造 kD 樹的方法，如采樣，再結(jié)合實(shí)際的 3D 模型來為大家說明具體的操作方法。

基本概念：

　　由于 kD 樹主要用于光線跟蹤等 3D 圖形學(xué)領(lǐng)域，所以很有必要把光線跟蹤的基本方法弄清楚。我們知道場景都是由三角形組成，整個(gè)空間的三角形組成了模型的拓?fù)浣Y(jié)構(gòu)。傳統(tǒng)的光柵化過程就是把所有變換過的三角形投射到屏幕上，也就是寫入幀緩沖。而光線跟蹤的最初概念來自于繪畫。 15 世紀(jì)意大利 Albrecht D?rer 發(fā)明了網(wǎng)格作畫的方法，也就是在待畫的物體前放一張同畫布一樣大小的紙質(zhì)半透明網(wǎng)格，然后依次透過每個(gè)小格看物體，繪制那個(gè)小格子的圖畫，當(dāng)把所有的小格子都畫滿了后，一幅畫也就畫好了。

　　我們由此可以想到暴力測試法，也就是從一個(gè)網(wǎng)格里發(fā)出光線后，檢測場景中每個(gè)三角形，然后確定點(diǎn)亮那個(gè)網(wǎng)格（像素）的是什么顏色。 kD 樹可以大幅度加速這個(gè)過程，類似于二叉樹的遍歷。

準(zhǔn)備材料：

　　在真實(shí)的實(shí)現(xiàn)過程中，我們總是要面對許多模型的格式，比如 D3D 的 X 格式， QUAKE 系列所使用的 MD3/5 模型格式，以及諸多初學(xué)者所頭疼的 3DS ASE 格式。需要補(bǔ)充的是，如果牽涉到在場景中使用骨骼動(dòng)畫，那么只有選擇 MD5 或者 X 格式， 3DS/ASE 文件中沒有記錄骨骼動(dòng)畫所需要的權(quán)重節(jié)點(diǎn)等數(shù)據(jù)。

　　對于靜態(tài)模型來說，主要數(shù)據(jù)包括：頂點(diǎn)數(shù)據(jù)，三角形索引，紋理坐標(biāo)，頂點(diǎn)向量（有可能沒有）。繪制模型的時(shí)候，用三角形索引來尋址，依次抽取頂點(diǎn)數(shù)組中的數(shù)據(jù)進(jìn)行繪制。為了縮短開發(fā)周期，我們使用了來自 sourceforge.net 的 lib3ds[2] 開源庫來處理 3DS 模型。如圖：

　　這個(gè) Hanana 模型由 10955 個(gè)頂點(diǎn)， 16221 個(gè)面（三角形）組成。我們用它來生成我們所需要的 kD 樹加速結(jié)構(gòu)。

思路優(yōu)先：

　　我們的 kD 樹的節(jié)點(diǎn)模型究竟應(yīng)該是什么樣子的呢？讓我們看一下定義：

struct?kDInner{
unsigned?int?flagDimAndOffset;
//?bits?0..1?:?0?1?2代表x?y?z維
//?bits?2..30?:?offset?to?left?child
//?bit?31?:?是否是leaf
float?splitCoordinates;
};

struct?kDLeaf{
unsigned?int?flagAndOffset;
//?bits?0..30?:?在三角形數(shù)組組中的偏移量
//?bit?31?:?是否是leaf
unsigned?int?objectCount;//?三角形樹的數(shù)目
};

typedef?union{
kDLeaf?leaf;
kDInner?inner;
}kDNode;?//共用體，統(tǒng)inner和leaf統(tǒng)稱為為Node

??? 事實(shí)上，這樣一上來就如此的精簡并不方便構(gòu)建kD樹，我們先用普通的容易理解的定義表現(xiàn)一個(gè)Node

union?offsetorsplitpos{
???? float ?SplitPos;
???? ulong ?AbsoluteOffset;
};

struct ?KDNode
{
????KDNode * ?Left;
????KDNode * ?Right;
????offsetorsplitpos?tag;
???? ulong ?Count;//當(dāng)這個(gè)節(jié)電作為Inner使用的時(shí)候，Count儲存了Dimsion
};

　　每個(gè)三角形的 AABB(Axis Aligned Bounding Box 即軸對稱綁定盒 ) 也是必不可少的結(jié)構(gòu)。 AABB 就很簡單了，可以定義成這樣：

struct AABB{
float min[3],max[3];
};

　　我們之所以要把每個(gè)三角形都打散，是為了計(jì)算合適的 Split Plane 位置，你可以想象為從什么地方把場景分成兩半，也就是把一堆三角形分成兩部分，代碼級的思路就是，計(jì)算合適的數(shù)組偏移量。那么什么叫做合適的呢？請看下面的這個(gè)公式 [3] ：

??? 看似好像很復(fù)雜，其實(shí)可以化簡為這樣的公式：

在這里， Ct 指遍歷整個(gè)節(jié)點(diǎn)包含的三角形遍歷時(shí)間，也就是渲染這一簇三角形的時(shí)間； Cl 指 Split Plane“ 左邊”的三角形遍歷時(shí)間，同理 Cr 是“右邊”的遍歷時(shí)間。引用的一些資料認(rèn)為，

　　事實(shí)上， Cost(x) 是兩個(gè)單調(diào)函數(shù) Cl(x) 、 Cr(x) 的線性疊加。我們要盡量找到 Cost(x) 最小的某個(gè)空間位置，或者是某一個(gè)三角形邊界，進(jìn)而分割場景三角形。

　　顯然，這肯定由三步組成：

１、選擇合適的 Split Plane ，可以有三個(gè)維度，并且可以容易推斷總共有 2n 個(gè)

２、數(shù)數(shù)看左邊有多少個(gè) AABBs

３、數(shù)數(shù)看右邊有多少個(gè) AABBs

　　下面我們開始討論 2 種方法：排序與掃描。

Sort 排序

　　排序很容易理解。沿著軸將所有三角形的 AABB 排序（也就是對三角形索引數(shù)組進(jìn)行排序）。排序后就可以直接把想要得位置和三角形數(shù)目帶入公式計(jì)算，如果繪制為函數(shù)圖像可以獲得最光滑連續(xù)的圖形。總花費(fèi)為 O(nlogn) 。

Scan 掃描

　　掃描有些羅嗦，不過也很容易實(shí)現(xiàn)，最重要的是目前已經(jīng)有成功的應(yīng)用 [4] 。指定場景中的一個(gè)平面，遍歷三角形比較大小，記錄落在左邊和右邊的數(shù)目，再帶入公式。如果要獲得多個(gè) Cost 數(shù)值，就必須要選擇多個(gè)位置進(jìn)行計(jì)算。每次都要遍歷全部的三角形。經(jīng)過處理后也可以達(dá)到 O(nlogn) 的復(fù)雜度，不過結(jié)合了采樣技術(shù)后可以獲得近似準(zhǔn)確的結(jié)果，而且花費(fèi)小的多。而且，這個(gè)過程是可以使用 SIMD 加速的。

　　還有一些技巧和疑問 [3] ：

１、是否總是計(jì)算三個(gè)軸中最小的那個(gè)位置，還是總是從一個(gè)軸計(jì)算？

２、樹需要細(xì)分到何種程度？每個(gè) Leaf 需要有多少個(gè)三角形？

　　現(xiàn)在我們可以做進(jìn)一步的推測，如果希望用光線跟蹤一個(gè)動(dòng)態(tài)的場景，那么每當(dāng)我們變換過矩陣后，都需要重新構(gòu)造一次 kD 樹，所以為了達(dá)到實(shí)時(shí)交互式的速度，必須要對關(guān)鍵的步驟進(jìn)行優(yōu)化。而且生成樹的質(zhì)量與遍歷的性能關(guān)系十分密切。

　　我們的思路有了，下面可以構(gòu)思具體的實(shí)現(xiàn)過程

A. 準(zhǔn)備三角形索引數(shù)組 Tris[] 。
B. 獲得整個(gè)場景的 AABB V ，其中 V.min[0] 就是場景的左邊界，以此類推。
C. 通過三角形索引數(shù)組讀取 3 個(gè)頂點(diǎn)，構(gòu)造每個(gè)三角形的 AABB ，儲存到一個(gè)容器中 vector<AABB> AABBs ，同時(shí)記錄 AABB 究竟屬于哪個(gè)三角形。
D. 獲得三角形 AABBs 的數(shù)目 N ，如果大于一個(gè)數(shù)值比如 1024 就用步驟 FG 計(jì)算 3 次，否則只計(jì)算一次。獲得 AABBs 的開頭和末尾指針（迭代器）。
E. 如果選擇 Sort ，那么就要先對 AABBs 中的元素排序。這里我們采用 Scan 。
F. 在 (min[AXIS],max[AXIS]) 之間找?guī)讉€(gè)固定平面，比如 8 個(gè)。 AXIS 指選擇的坐標(biāo)軸。
H. 帶入公式計(jì)算，選擇 Cost 最小的 Split Position ，生成 Node 。如果已經(jīng)達(dá)到中止條件，那么就生成 Leaf Node ，否則生成 Inner Node 。把 v 從 Split Position 分成兩個(gè) Voxel Vl 與 Vr 。把 AABBs 分割為兩個(gè)，從與 Split Position 最近的三角形開始。
G. 遍歷 AABBs 容器，比較平面和每個(gè)元素的位置，記錄 8 對數(shù)據(jù)。
I. 帶入 Vl 與 Vr 分別從 D 開始迭代。

??? 下面是分隔這個(gè)模型的輸出信息：

TriNum?:? 16220
Left?Voxel?has?:? 12377 ??Right?Voxel?has?:? 384
Left?Voxel?has?:? 2912 ???Right?Voxel?has?:? 946
Left?Voxel?has?:? 1025 ???Right?Voxel?has?:? 188
Left?Voxel?has?:? 415 ????Right?Voxel?has?:? 610
Left?Voxel?has?:? 128 ????Right?Voxel?has?:? 287
Left?Voxel?has?:? 68 ?????Right?Voxel?has?:? 60
Leaf?LEVEL?:? 5 ??Count?:? 128
Left?Voxel?has?:? 145 ????Right?Voxel?has?:? 142
Left?Voxel?has?:? 77 ?????Right?Voxel?has?:? 68
Leaf?LEVEL?:? 6 ??Count?:? 145
Left?Voxel?has?:? 61 ?????Right?Voxel?has?:? 81
Leaf?LEVEL?:? 6 ??Count?:? 142
Left?Voxel?has?:? 218 ????Right?Voxel?has?:? 392
Left?Voxel?has?:? 97 ?????Right?Voxel?has?:? 121
Leaf?LEVEL?:? 5 ??Count?:? 218
Left?Voxel?has?:? 211 ????Right?Voxel?has?:? 181
Left?Voxel?has?:? 114 ????Right?Voxel?has?:? 97
Leaf?LEVEL?:? 6 ??Count?:? 211
Left?Voxel?has?:? 82 ?????Right?Voxel?has?:? 99
Leaf?LEVEL?:? 6 ??Count?:? 181
Left?Voxel?has?:? 772 ????Right?Voxel?has?:? 111
Left?Voxel?has?:? 373 ????Right?Voxel?has?:? 399
Left?Voxel?has?:? 194 ????Right?Voxel?has?:? 179
Left?Voxel?has?:? 82 ?????Right?Voxel?has?:? 112
Leaf?LEVEL?:? 6 ??Count?:? 194
Left?Voxel?has?:? 111 ????Right?Voxel?has?:? 68
Leaf?LEVEL?:? 6 ??Count?:? 179
Left?Voxel?has?:? 190 ????Right?Voxel?has?:? 209
Left?Voxel?has?:? 99 ?????Right?Voxel?has?:? 91
Leaf?LEVEL?:? 6 ??Count?:? 190
Left?Voxel?has?:? 63 ?????Right?Voxel?has?:? 146
Left?Voxel?has?:? 516 ????Right?Voxel?has?:? 599
Left?Voxel?has?:? 246 ????Right?Voxel?has?:? 270
Left?Voxel?has?:? 124 ????Right?Voxel?has?:? 122
Leaf?LEVEL?:? 6 ??Count?:? 246
Left?Voxel?has?:? 126 ????Right?Voxel?has?:? 144
Left?Voxel?has?:? 285 ????Right?Voxel?has?:? 314
Left?Voxel?has?:? 150 ????Right?Voxel?has?:? 135
Left?Voxel?has?:? 152 ????Right?Voxel?has?:? 162
Left?Voxel?has?:? 4180 ???Right?Voxel?has?:? 528
Left?Voxel?has?:? 2220 ???Right?Voxel?has?:? 196
Left?Voxel?has?:? 1211 ???Right?Voxel?has?:? 100
Left?Voxel?has?:? 502 ????Right?Voxel?has?:? 709
Left?Voxel?has?:? 235 ????Right?Voxel?has?:? 267
Left?Voxel?has?:? 343 ????Right?Voxel?has?:? 366
Left?Voxel?has?:? 471 ????Right?Voxel?has?:? 538
Left?Voxel?has?:? 201 ????Right?Voxel?has?:? 270
Left?Voxel?has?:? 263 ????Right?Voxel?has?:? 275
Left?Voxel?has?:? 924 ????Right?Voxel?has?:? 103
Left?Voxel?has?:? 428 ????Right?Voxel?has?:? 496
Left?Voxel?has?:? 184 ????Right?Voxel?has?:? 244
Left?Voxel?has?:? 286 ????Right?Voxel?has?:? 210
Left?Voxel?has?:? 440 ????Right?Voxel?has?:? 596
Left?Voxel?has?:? 211 ????Right?Voxel?has?:? 229
Left?Voxel?has?:? 310 ????Right?Voxel?has?:? 286
Left?Voxel?has?:? 2437 ???Right?Voxel?has?:? 284
Left?Voxel?has?:? 1228 ???Right?Voxel?has?:? 120
Left?Voxel?has?:? 558 ????Right?Voxel?has?:? 670
Left?Voxel?has?:? 303 ????Right?Voxel?has?:? 255
Left?Voxel?has?:? 298 ????Right?Voxel?has?:? 372
Left?Voxel?has?:? 578 ????Right?Voxel?has?:? 631
Left?Voxel?has?:? 295 ????Right?Voxel?has?:? 283
Left?Voxel?has?:? 302 ????Right?Voxel?has?:? 329
Left?Voxel?has?:? 1466 ???Right?Voxel?has?:? 138
Left?Voxel?has?:? 805 ????Right?Voxel?has?:? 661
Left?Voxel?has?:? 430 ????Right?Voxel?has?:? 375
Left?Voxel?has?:? 346 ????Right?Voxel?has?:? 315
Left?Voxel?has?:? 653 ????Right?Voxel?has?:? 729
Left?Voxel?has?:? 347 ????Right?Voxel?has?:? 306
Left?Voxel?has?:? 367 ????Right?Voxel?has?:? 362
Left?Voxel?has?:? 2319 ???Right?Voxel?has?:? 152
Left?Voxel?has?:? 1413 ???Right?Voxel?has?:? 906
Left?Voxel?has?:? 825 ????Right?Voxel?has?:? 588
Left?Voxel?has?:? 437 ????Right?Voxel?has?:? 388
Left?Voxel?has?:? 180 ????Right?Voxel?has?:? 257
Left?Voxel?has?:? 98 ?????Right?Voxel?has?:? 82
Leaf?LEVEL?:? 6 ??Count?:? 180
Left?Voxel?has?:? 150 ????Right?Voxel?has?:? 107
Left?Voxel?has?:? 191 ????Right?Voxel?has?:? 197
Left?Voxel?has?:? 90 ?????Right?Voxel?has?:? 101
Leaf?LEVEL?:? 6 ??Count?:? 191
Left?Voxel?has?:? 68 ?????Right?Voxel?has?:? 129
Left?Voxel?has?:? 294 ????Right?Voxel?has?:? 294
Left?Voxel?has?:? 150 ????Right?Voxel?has?:? 144
Left?Voxel?has?:? 91 ?????Right?Voxel?has?:? 59
Leaf?LEVEL?:? 6 ??Count?:? 150
Left?Voxel?has?:? 51 ?????Right?Voxel?has?:? 93
Leaf?LEVEL?:? 6 ??Count?:? 144
Left?Voxel?has?:? 153 ????Right?Voxel?has?:? 141
Left?Voxel?has?:? 105 ????Right?Voxel?has?:? 48
Leaf?LEVEL?:? 6 ??Count?:? 153
Left?Voxel?has?:? 49 ?????Right?Voxel?has?:? 92
Leaf?LEVEL?:? 6 ??Count?:? 141
Left?Voxel?has?:? 457 ????Right?Voxel?has?:? 449
Left?Voxel?has?:? 214 ????Right?Voxel?has?:? 243
Left?Voxel?has?:? 124 ????Right?Voxel?has?:? 90
Leaf?LEVEL?:? 5 ??Count?:? 214
Left?Voxel?has?:? 102 ????Right?Voxel?has?:? 141
Left?Voxel?has?:? 79 ?????Right?Voxel?has?:? 62
Leaf?LEVEL?:? 6 ??Count?:? 141
Left?Voxel?has?:? 196 ????Right?Voxel?has?:? 253
Left?Voxel?has?:? 99 ?????Right?Voxel?has?:? 97
Leaf?LEVEL?:? 5 ??Count?:? 196
Left?Voxel?has?:? 133 ????Right?Voxel?has?:? 120
Left?Voxel?has?:? 56 ?????Right?Voxel?has?:? 77
Leaf?LEVEL?:? 6 ??Count?:? 133
Left?Voxel?has?:? 791 ????Right?Voxel?has?:? 733
Left?Voxel?has?:? 462 ????Right?Voxel?has?:? 329
Left?Voxel?has?:? 228 ????Right?Voxel?has?:? 234
Left?Voxel?has?:? 129 ????Right?Voxel?has?:? 99
Left?Voxel?has?:? 64 ?????Right?Voxel?has?:? 65
Leaf?LEVEL?:? 6 ??Count?:? 129
Left?Voxel?has?:? 117 ????Right?Voxel?has?:? 117
Leaf?LEVEL?:? 5 ??Count?:? 234
Left?Voxel?has?:? 171 ????Right?Voxel?has?:? 158
Left?Voxel?has?:? 90 ?????Right?Voxel?has?:? 81
Leaf?LEVEL?:? 5 ??Count?:? 171
Left?Voxel?has?:? 88 ?????Right?Voxel?has?:? 70
Leaf?LEVEL?:? 5 ??Count?:? 158
Left?Voxel?has?:? 423 ????Right?Voxel?has?:? 310
Left?Voxel?has?:? 205 ????Right?Voxel?has?:? 218
Left?Voxel?has?:? 114 ????Right?Voxel?has?:? 91
Leaf?LEVEL?:? 5 ??Count?:? 205
Left?Voxel?has?:? 112 ????Right?Voxel?has?:? 106
Leaf?LEVEL?:? 5 ??Count?:? 218
Left?Voxel?has?:? 177 ????Right?Voxel?has?:? 133
Left?Voxel?has?:? 86 ?????Right?Voxel?has?:? 91
Leaf?LEVEL?:? 5 ??Count?:? 177
Left?Voxel?has?:? 77 ?????Right?Voxel?has?:? 56
Leaf?LEVEL?:? 5 ??Count?:? 133

　　其中， C 可以用 foreach ， H 可以用 partition （ stable_partition ）等 STL 的算法。

核心的代碼如下：

void ?Count(AABB * ?BeginItr,AABB * ?EndItr,AXIS?Axis, float ?SplitPos, ulong * ?Cl, ulong * ?Cr)
{
???? for (?AABB * ?itr? = ?BeginItr?;?itr? != ?EndItr;?itr ++ ?){
????????( * Cl) += (?(itr -> max[Axis]? < ?SplitPos?)? ? ? 1 ?:? 0 ?);
????????( * Cr) += (?(itr -> min[Axis]? > ?SplitPos?)? ? ? 1 ?:? 0 ?);
????}
};

inline? bool ?Terminate( ulong ?TriCount, int ?Level)
{
???? if ?(?TriCount? < ? 128 ? || ?Level? > ?MAX_LEVEL){
???????? return ? true ;
????}
???? return ? false ;
};

inline? bool ?IsUpboundSmaller(AABB & ?AABB)
{
???? float ?half_width? = ?(?AABB.max[::gSplitAxis]? - ?AABB.min[::gSplitAxis]?) * 0.5f ;
???? return ?(AABB.max[::gSplitAxis]? - ?::gSplitPos)? < ?half_width? ? ? true ?:? false ;
};

float ?SAHCost(AXIS?Axis, ulong * ?Cl, ulong * ?Cr,AABB & ?V, float ?SplitPos)
{
???? ulong ?Nl? = ? * Cl;
???? ulong ?Nr? = ? * Cr;
???? float ?Length? = ?V.max[Axis]? - ?V.min[Axis];
???? float ?L? = ?SplitPos? - ?V.min[Axis],R? = ?SplitPos? - ?V.max[Axis];
???? float ?Pl? = ?L? / ?Length;
???? float ?Pr? = ? 1.0f ? - ?Pl;
???? float ?Tt? = ?TRAVERSAL_TIME;
???? float ?Til? = ?Nl? * ?INTERSECTION_TIME,Tir? = ?Nr? * ?INTERSECTION_TIME;
???? return ?Tt? + ?Pl * Nl * Til? + ?Pr * Nr * Tir;

};

void ?KDTreeBuild(KDNode * ?Root,AABB?V,AABB * ?BeginItr,AABB * ?EndItr,AXIS?Axis, int ?Level)
{
???? ulong ?TotalTriCount? = ?EndItr? - ?BeginItr;
???? if (?Terminate(TotalTriCount,Level)?)
???????? return ;

???? float ?SplitLoc[ 7 ];
???? float ?Cost[ 7 ];

???? ulong ?Cl? = ? 0 ,Cr? = ? 0 ;
???? float ?MinLoc? = ?V.min[Axis],MaxLoc? = ?V.max[Axis];
???? float ?step? = ?(MaxLoc? - ?MinLoc)? / ? 8.0f ;

???? for (? int ?i? = ? 0 ;i < 7 ?;i ++ ?){
????????SplitLoc[i]? = ?MinLoc? + ?step? * ? float (i + 1 );
????????Count(BeginItr,EndItr,Axis,SplitLoc[i], & Cl, & Cr);
????????Cost[i]? = ?SAHCost(Axis, & Cl, & Cr,V,SplitLoc[i]);
????????Cl? = ?Cr? = ? 0 ;
????}
???? float * ?pGoodCostPtr? = ?min_element(Cost,Cost + 7 );
????size_t?_Pos? = ?pGoodCostPtr? - ?Cost;

????::gSplitPos? = ?SplitLoc[_Pos];
????::gSplitAxis? = ?Axis;

????AABB * ?MidItr? = ?stable_partition(BeginItr,EndItr,IsUpboundSmaller);

????Cl? = ?MidItr? - ?BeginItr;
????Cr? = ?EndItr? - ?MidItr;

????cout << " Left?Voxel?has?:? " << Cl << " \tRight?Voxel?has?:? " << Cr << endl;

????AABB?Vl,Vr;

???? if ?(?Cr? > ? 128 ? || ?Cl? > ? 128 ?){
????????Root? = ? new ?KDNode;? // Root

????????Root -> Left? = ? new ?KDNode;
????????Root -> Right? = ? new ?KDNode;

????????Root -> tag.SplitPos? = ?::gSplitPos;
????????Root -> Count? = ?Axis; // Ulong.MaxSize?-?Axis?代表坐標(biāo)?因?yàn)長eft?Right肯定不是0
???????? switch (Axis){
???????????? case ?X?:
????????????????Vl.min[ 0 ]? = ?V.min[ 0 ];
????????????????Vl.min[ 1 ]? = ?V.min[ 1 ];
????????????????Vl.min[ 2 ]? = ?V.min[ 2 ];
????????????????Vl.max[ 0 ]? = ?::gSplitPos;
????????????????Vl.max[ 1 ]? = ?V.max[ 1 ];
????????????????Vl.max[ 2 ]? = ?V.max[ 2 ];

????????????????Vr.min[ 0 ]? = ?::gSplitPos;
????????????????Vr.min[ 1 ]? = ?V.min[ 1 ];
????????????????Vr.min[ 2 ]? = ?V.min[ 2 ];
????????????????Vr.max[ 0 ]? = ?V.max[ 0 ];
????????????????Vr.max[ 1 ]? = ?V.max[ 1 ];
????????????????Vr.max[ 2 ]? = ?V.max[ 2 ];
???????????????? break ;
???????????? case ?Y?:
????????????????Vl.min[ 0 ]? = ?V.min[ 0 ];
????????????????Vl.min[ 1 ]? = ?V.min[ 1 ];
????????????????Vl.min[ 2 ]? = ?V.min[ 2 ];
????????????????Vl.max[ 0 ]? = ?V.max[ 0 ];
????????????????Vl.max[ 1 ]? = ?::gSplitPos;
????????????????Vl.max[ 2 ]? = ?V.max[ 2 ];

????????????????Vr.min[ 0 ]? = ?V.min[ 0 ];
????????????????Vr.min[ 1 ]? = ?::gSplitPos;
????????????????Vr.min[ 2 ]? = ?V.min[ 2 ];
????????????????Vr.max[ 0 ]? = ?V.max[ 0 ];
????????????????Vr.max[ 1 ]? = ?V.max[ 1 ];
????????????????Vr.max[ 2 ]? = ?V.max[ 2 ];
???????????????? break ;
???????????? case ?Z?:
????????????????Vl.min[ 0 ]? = ?V.min[ 0 ];
????????????????Vl.min[ 1 ]? = ?V.min[ 1 ];
????????????????Vl.min[ 2 ]? = ?V.min[ 2 ];
????????????????Vl.max[ 0 ]? = ?V.max[ 0 ];
????????????????Vl.max[ 1 ]? = ?V.max[ 1 ];
????????????????Vl.max[ 2 ]? = ?::gSplitPos;

????????????????Vr.min[ 0 ]? = ?V.min[ 0 ];
????????????????Vr.min[ 1 ]? = ?V.min[ 1 ];
????????????????Vr.min[ 2 ]? = ?::gSplitPos;
????????????????Vr.max[ 0 ]? = ?V.max[ 0 ];
????????????????Vr.max[ 1 ]? = ?V.max[ 1 ];
????????????????Vr.max[ 2 ]? = ?V.max[ 2 ];
???????????????? break ;
????????}
????} else {
????????Root? = ? new ?KDNode;? // Leaf
????????Root -> Left? = ? 0 ;Root -> Right? = ? 0 ;
????????Root -> tag.AbsoluteOffset? = ?BeginItr? - ?::gScenePtr;
????????Root -> Count? = ?EndItr? - ?BeginItr;
??????? //cout << " Leaf?LEVEL?:? " << Level << " \tCount?:? " << Root -> Count << endl;
???????? return ;
????}
???? ++ Level;
????KDTreeBuild(Root -> Left,Vl,BeginItr,MidItr,Axis,Level);
????KDTreeBuild(Root -> Right,Vr,MidItr,EndItr,Axis,Level);
};

??? 這樣，我們就得到了一顆完整的基于SAH的KD樹。下面就是遍歷。

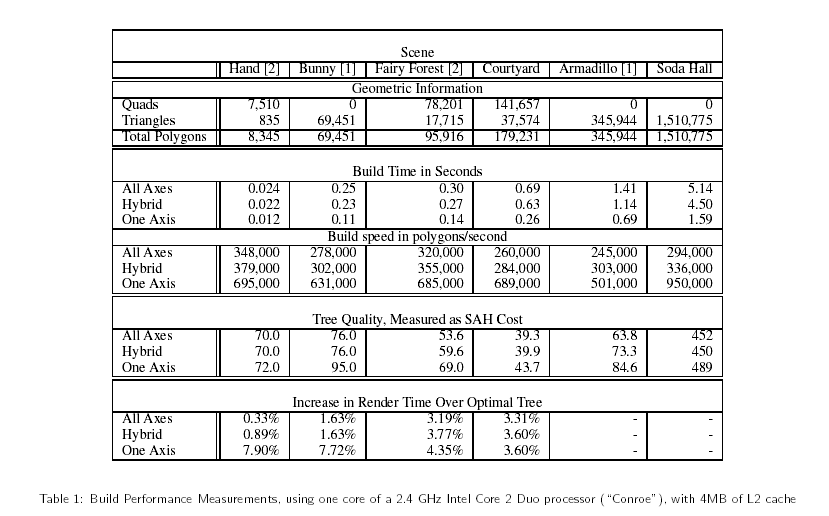
　　由于不同渲染要求的不同，遍歷代碼也大不相同。不過我們可以知道，kD樹及適用于光線跟蹤程序。目前在多款開源光線跟蹤器，比如blender就采用了kD樹作為加速結(jié)構(gòu)。而且必須要提到的是，如果希望在Realtime Rendering的程序中使用光線跟蹤技術(shù) —— 雖然說在目前的情況下還不是很現(xiàn)實(shí)，不過這畢竟是個(gè)趨勢，因?yàn)橹挥泄饩€跟蹤才能夠精確的模擬物理全局光照，光柵化系統(tǒng)先天限制無法達(dá)到，雖然說Voxel渲染是一個(gè)折中的辦法。我引用下面的這張表格[3]作為性能參照。

　　可是這里又會(huì)出現(xiàn)一個(gè)問題，就是在實(shí)時(shí)渲染程序中如何處理多紋理貼圖？我們必須要模擬管線的處理過程。

A、如果場景中有運(yùn)動(dòng)的模型，標(biāo)記出來

B、在世界坐標(biāo)系統(tǒng)中對運(yùn)動(dòng)模型作矩陣變換，類似于OpenGL的MATRIX操作

C、把所有，各就各位的模型頂點(diǎn)、向量、紋理坐標(biāo)、索引整合在一起。每當(dāng)在這個(gè)鏈表中加入新的模型的時(shí)候，都要把現(xiàn)在模型的所有索引加上鏈表中已經(jīng)加入的所有頂點(diǎn)的數(shù)目，構(gòu)建一個(gè)好像是整體連續(xù)的單個(gè)模型。同時(shí)標(biāo)記紋理，應(yīng)該儲存一個(gè)頂點(diǎn)偏移量以及三角形數(shù)目，用來標(biāo)示這個(gè)紋理屬于哪個(gè)模型。

D、根據(jù)視點(diǎn)，遍歷kD樹，把符合條件的三角形數(shù)目放入一個(gè)全局隊(duì)列

E、渲染隊(duì)列中的所有三角形，作為一個(gè)Frame。重復(fù)A。

　　目前由德國薩爾大學(xué)計(jì)算機(jī)科學(xué)系所開發(fā)的實(shí)時(shí)光線跟蹤硬件與軟件已經(jīng)成功的問世，最令人振奮的莫過于表現(xiàn)了一個(gè)全部由光線跟蹤引擎實(shí)現(xiàn)的Quake3游戲。有興趣的朋友可以去[4]看看。

[1]Computer Graphics WS05/06 – kD-Tree and Optimization for Ray Tracing
[2]Lib3ds http://lib3ds.sf.net/
[3]Fast kd-tree Construction with an Adaptive Error-Bounded Heuristic

[4]OpenRT http://www.openrt.de/

posted on 2007-02-15 22:31 周波閱讀(3512) 評論(2) 編輯收藏引用所屬分類: Cg藝術(shù) 、無庸技術(shù)

FeedBack:

# re: 利用SAH實(shí)現(xiàn)kD樹快速分割模型實(shí)踐

2007-02-16 14:59 | AIBPXTSHMF

bobo，這幾天研究kd樹的結(jié)果吧回復(fù) 更多評論

# re: 利用SAH實(shí)現(xiàn)kD樹快速分割模型實(shí)踐

2007-09-03 09:14 | freesky

很精彩，不過資料再多點(diǎn)就好了回復(fù) 更多評論

刷新評論列表

只有注冊用戶登錄后才能發(fā)表評論。
【推薦】100%開源！大型工業(yè)跨平臺軟件C++源碼提供，建模，組態(tài)！

相關(guān)文章: Pure GPU Computing Platform : NVIDIA CUDA Tutorial 利用SAH實(shí)現(xiàn)kD樹快速分割模型實(shí)踐 Progressive Mesh 矩陣圣經(jīng) FOR 3D Computer Graphic Final BattleField 2142引擎圖形程序員小訪談 GPU還可以做什么 —— Brook for GPUs,Stream Computing On GPUs

網(wǎng)站導(dǎo)航: 博客園 IT新聞 BlogJava 博問 Chat2DB 管理

2025年5月

日

一

二

三

四

五

六

周波 87年出生南京林業(yè)大學(xué)05421班242信箱專業(yè)木材科學(xué)與工程工業(yè)裝備與過程自動(dòng)化遷移到 jedimaster(dot)cnblogs(dot)com

常用鏈接

留言簿(4)

隨筆分類

隨筆檔案

新聞檔案

2007年1月 (1)

同學(xué)們Blog

Rita的QZONE
隊(duì)長的BLOG
海翎的BLOG
胡小松的Blog
君胖的Blog
貓貓的BLOG
丫頭的BLOG
左圓的BLOG

搜索

積分與排名

積分 - 54161
排名 - 421