本文簡單簡介二叉樹的概念，并給出平衡一顆二叉樹的方法

關于二叉樹
    現(xiàn)在有N個元素的數(shù)組或者鏈表，要查找一個元素必須遍歷數(shù)組直到找到元素。假如元素在是數(shù)組中最后一個或者數(shù)組中不存在這樣的元素，那么很不幸，我們要遍歷整個數(shù)組。如果N非常大，那將是非常痛苦的一件事情。
用二叉樹情況就好多了：
1． 更快的查找
2． 增加元素時，元素被自動排列
原理：
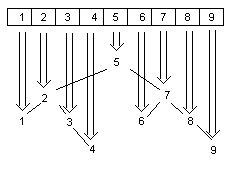
在鏈表或數(shù)組中，元素一個接著一個，如圖


 

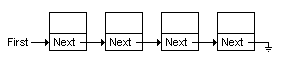
在二叉樹中情況不太一樣了


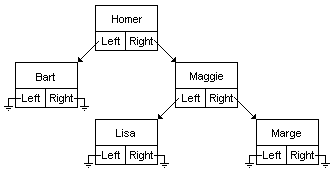
每個元素連著兩個元素，左孩子和右孩子。他們存儲的值的關系有如下規(guī)定
Value（left）<Value（middle）<=Value（right）

排序：
在二叉樹中利用遞歸你能很方便的排序
前序遍歷
PrintElement(pTopMostElement)
   .
   .
  void PrintElement(TreeElement* pElement)
  {
    if (pElement)
    {
      PrintElement(pElement->LeftChild)
      pElement->PrintMe()
      PrintElement(pElement->RightChild)
    }
  }

后序遍歷：

PrintElementReversed(pTopMostElement)
   .
   .
  void PrintElementReversed(TreeElement* pElement)
  {
    if (pElement)
    {
      PrintElementReversed(pElement->RightChild)
      pElement->PrintMe()
      PrintElementReversed(pElement->LeftChild)
    }
  }

如何使二叉樹平衡？
添加元素的順序將影響二叉樹的形態(tài)，以3,6,4,8,1,9,2,7,5的順序得到

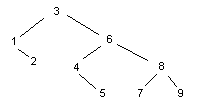
以1,2,3,4,5,6,7,8,9將得到

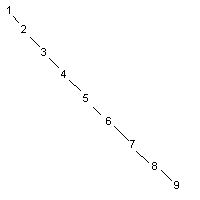
有以下方法可以考慮：
1． 以非排序的元素插入元素，不能要求給出的元素是高度不排序的
2． 以一組隨機元素構造二叉樹，然后替換這些元素，然后通過旋轉得到平衡的樹。參考隨機樹。
3． 重構這稞樹

重構整稞樹
1． 把元素拷貝到數(shù)組中，以升序排序
2． 清空這棵樹
3． 從數(shù)組中高度不排序的選取元素插入樹中可以這樣完成第三步：


可以遞歸的實現(xiàn)：
// Assuming array ranges from [0..arraySize-1]
GetFromOrderedArray(0,arraySize-1)
  .
  .
void GetFromOrderedArray(int lowBound,int highBound)
{
  if (hi < low) return;
  middlePos = lowBound+(highBound-lowBound)/2
  // middlePos is now at the element in the middle
  // between lowBound and highBound, so we just add
  // it to the tree

  AddElement ( theOrderedArray[middlePos] )

  // Pick the middle one "to the left"
  AddFromOrderedArray(lowBound,middlePos-1)

  // Pick the middle one "to the right"
  AddFromOrderedArray(middlePos+1,highBound)
}


刪除一個元素

首先要找到要刪除的元素E，有兩種方法：
1． 通過遍歷找到這個元素E
2． 給每個元素一個指向雙親的指針

接下來就是刪除的過程了：
1． 剪斷E與他雙親的連接
2． 將左右孩子所在的子樹同其他元素一樣加到樹中
3． 刪除E

void RemoveElement(TreeElement* theOneToRemove)
{
  TreeElement* pParent = theOneToRemove->GetParent();

  // Ok, so it has a parent, then we'll simply just disconnect it.
  if (pParent)
  {
     if (pParent->GetLeftChild() == theOneToRemove)
     {
        pParent->SetLeftChild(NULL);
     }
     else
     {
        ASSERT(pParent->GetRightChild() == theOneToRemove);
        pParent->SetRightChild(NULL);
     }
  }
  else
  {
     // No parent? Then we're removing the root element.
     theTopMostElement = NULL;
   }

  // Disconnected, now we reconnect its children (if any)
  // just by adding them as we add any other node.
  if (theOneToRemove->GetLeftChild())
   AddElement(theOneToRemove->GetLeftChild());
  if (theOneToRemove->GetRightChild())
   AddElement(theOneToRemove->GetRightChild());

  //Zap the element (if that's what you want to do)
  delete theOneToRemove;

}

注解：

通過函數(shù)回調(diào) 遍歷二叉樹

注：函數(shù)回調(diào)例如AddElement(theOneToRemove->GetRightChild());

簡而言之，回調(diào)函數(shù)就是一個通過函數(shù)指針調(diào)用的函數(shù)。如果你把函數(shù)的指針（地址）作為參數(shù)傳遞給另一個函數(shù)，當這個指針被用為調(diào)用它所指向的函數(shù)時，我們就說這是回調(diào)函數(shù)。
可以把調(diào)用者與被調(diào)用者分開。調(diào)用者不關心誰是被調(diào)用者，所有它需知道的，只是存在一個具有某種特定原型、某些限制條件（如返回值為int）的被調(diào)用函數(shù)。

                                            #內(nèi)容選自CodeGuru
若理解錯誤，歡迎指正！