久久免费少妇高潮久久精品99,在线亚洲自拍,久久久久女教师免费一区

CodeGuru代码阅读(一)

AIBPXTSHMF — Sun, 22 Jul 2007 04:27:00 GMT

本文��单简介二叉树的概念，�q�给出��^衡一颗二叉树的方�?/span>

关于二叉�?br> 现在�?/span>N个元素的数组或者链表，要查找一个元素必��遍历数�l�直到找到元素。假如元素在是数�l�中最后一个或者数�l�中不存在这��L��元素�Q�那么很不幸�Q�我们要遍历整个数组。如�?/span>N非常大，那将是非常痛苦的一件事情�?br>用二叉树情况��好多了�Q?br>1�Q?nbsp;更快的查�?br>2�Q?nbsp;增加元素�Ӟ��元素被自动排�?br>原理�Q?/em>
在链表或数组中，元素一个接着一个，如图

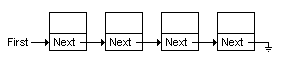
在二叉树中情况不太一样了

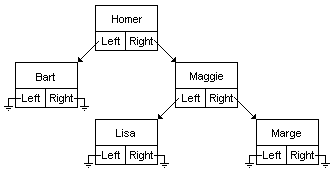
每个元素�q�着两个元素�Q�左孩子和右孩子。他们存储的值的关系有如下规�?br>Value�Q?/span>left�Q?/span>�Q?/span>middle�Q?/span><=Value�Q?/span>right�Q?br>
排序�Q?br>在二叉树中利用递归你能很方便的排序
前序遍历
PrintElement(pTopMostElement)
   .
   .
  void PrintElement(TreeElement* pElement)
  {
    if (pElement)
    {
      PrintElement(pElement->LeftChild)
      pElement->PrintMe()
      PrintElement(pElement->RightChild)
    }
  }

后序遍历�Q?/span>

PrintElementReversed(pTopMostElement)
   .
   .
  void PrintElementReversed(TreeElement* pElement)
  {
    if (pElement)
    {
      PrintElementReversed(pElement->RightChild)
      pElement->PrintMe()
      PrintElementReversed(pElement->LeftChild)
    }
  }

如何使二叉树�q��Q?/em>
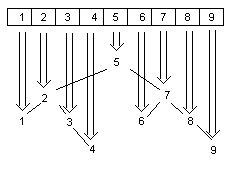
��d��元素的顺序将影响二叉树的形态，�?/span>3,6,4,8,1,9,2,7,5的顺序得�?/span>

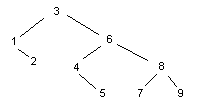
�?/font>1,2,3,4,5,6,7,8,9��得�?br>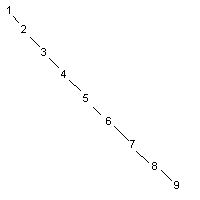
有以下方法可以考虑�Q?br>1�Q?span> 以非排序的元素插入元素，不能要求�l�出的元素是高度不排序的
2�Q?nbsp;以一�l�随机元素构造二叉树�Q�然后替换这些元素，然后通过旋�{得到�q��的树。参考随机树�?br>3�Q?nbsp;重构�q�稞�?br>
重构整稞�?br>1�Q?nbsp;把元素拷贝到数组中，以升序排�?br>2�Q?nbsp;清空�q�棵�?br>3�Q?nbsp;从数�l�中高度不排序的选取元素插入树中可以�q�样完成�W�三步：

可以递归的实玎ͼ�
// Assuming array ranges from [0..arraySize-1]
GetFromOrderedArray(0,arraySize-1)
  .
  .
void GetFromOrderedArray(int lowBound,int highBound)
{
  if (hi < low) return;
  middlePos = lowBound+(highBound-lowBound)/2
  // middlePos is now at the element in the middle
  // between lowBound and highBound, so we just add
  // it to the tree

  AddElement ( theOrderedArray[middlePos] )

  // Pick the middle one "to the left"
  AddFromOrderedArray(lowBound,middlePos-1)

  // Pick the middle one "to the right"
  AddFromOrderedArray(middlePos+1,highBound)
}

删除一个元�?br>

首先要找到要删除的元�?/span>E�Q�有两种�Ҏ��Q?br>1�Q?nbsp;通过遍历扑ֈ��q�个元素E
2�Q?nbsp;�l�每个元素一个指向双亲的指针

接下来就是删除的�q�程了：
1�Q?nbsp;剪断E与他双亲的连�?br>2�Q?nbsp;��左叛_��子所在的子树同其他元素一样加到树�?br>3�Q?nbsp;删除E

void RemoveElement(TreeElement* theOneToRemove)
{
  TreeElement* pParent = theOneToRemove->GetParent();

  // Ok, so it has a parent, then we'll simply just disconnect it.
  if (pParent)
  {
     if (pParent->GetLeftChild() == theOneToRemove)
     {
        pParent->SetLeftChild(NULL);
     }
     else
     {
        ASSERT(pParent->GetRightChild() == theOneToRemove);
        pParent->SetRightChild(NULL);
     }
  }
  else
  {
     // No parent? Then we're removing the root element.
     theTopMostElement = NULL;
   }

  // Disconnected, now we reconnect its children (if any)
  // just by adding them as we add any other node.
  if (theOneToRemove->GetLeftChild())
   AddElement(theOneToRemove->GetLeftChild());
  if (theOneToRemove->GetRightChild())
   AddElement(theOneToRemove->GetRightChild());

  //Zap the element (if that's what you want to do)
  delete theOneToRemove;

}

注解�Q?/span>
通过函数回调遍历二叉�?/span>
注：函数回调例如AddElement(theOneToRemove->GetRightChild());
��而言之，回调函数��是一个通过函数指针调用的函数。如果你把函数的指针�Q�地址�Q�作为参��C��递给另一个函敎ͼ�当这个指针被用�ؓ调用它所指向的函数时�Q�我们就说这是回调函数�?br>可以把调用者与被调用者分开。调用者不兛_��谁是被调用者，所有它需知道的，只是存在一个具有某�U�特定原型、某些限制条�Ӟ��如返回��gؓint�Q�的被调用函数�?br>
                                            #内容选自CodeGuru
若理解错误，�Ƣ迎指正�Q?/span>

AIBPXTSHMF 2007-07-22 12:27 发表评论

Euclid扩展��法

AIBPXTSHMF — Sun, 10 Jun 2007 10:25:00 GMT
满��d=gcd(a,b)=ax+by
gcd(b,a%b)=bx'+(a%b)y'=bx'+(a-(a/b)b)y'=bx'+ay'-b(a/b)y'=ay'+b(x'-(a/b)y')
只需满��
x=y'
y=x'-(a/b)y'

//d=gcd(a,b)=ax+by
#include<iostream>
using namespace std;
int extEuclid(int a,int b,int&x,int&y)
{
    int d,tmp;
    if(!b){x=1;y=0;return a;}
    d=extEuclid(b,a%b,x,y);
    tmp=x;
    x=y;
    y=tmp-(a/b)*y;
    return d;
}

int main(){
    int a,b,x=0,y=0;
    cin>>a>>b;//99 78
    cout<<extEuclid(a,b,x,y)<<'\t'<<x<<'\t'<<y;
    //system("pause");
    return 0;
}
奇怪的是VC6.0�~�译通过后执行，无论如何x和y的值始�l��ؓ0。而用dev�Q�c++�~�译通过后显�C�结果正常！
如果��输出改�?br>
cout<<extEuclid(a,b,x,y)<<endl;
    cout<<'\t'<<x<<'\t'<<y;
VC6.0�~�译后运行也��显�C�正�怺��Q?br>I DON'T KNOW WHY?

AIBPXTSHMF 2007-06-10 18:25 发表评论

AIBPXTSHMF — Tue, 05 Jun 2007 14:44:00 GMT
查了一下书,知道了这样一个公�?�q�样昨天二分法的疑问��可以解决了,也可以用�q�代法实��C��:看来吴文虎编写的书还挺配套的.

也就�?a^b%n=((a^b-1)*a)%n====>(a*b)%n=((a%n)*b)%n===>a^b%n=(((a^(b/2))%n)*a^(b/2))%n
//�q�代�?/span>
int modexp2(int a,int b,int n)
{
    int r;
    r=a%n;
    for(int i=0;i<b-1;i++)
        r=(r*a)%n;
    return r;
}
书中�q�说可以提高效率,研究后再�?
(a^b)%n=(a^�Q�b/2�Q?n * a^�Q�b/2�Q?n)%n
�Ҏ��q�个公式�Q�讨论奇数和偶数处理

int modExp(int a, int b, int n)
{
    int d=1,r=a;
    while(b){
        if(b%2==1){d=d*r%n;}
        r=r*r%n;
        b=b/2;
    }
    return d;
}

AIBPXTSHMF 2007-06-05 22:44 发表评论

AIBPXTSHMF — Sun, 03 Jun 2007 14:38:00 GMT

//(a^b)%n
#include<iostream>
//�q�里用的是什么方法呢?
int modExp(int a,int b,int n)
{
    int t=1,y=a;
    while(b)
    {
        if(b%2==1)t=t*y%n;
        y=y*y%n;
        b=b/2;
    }
    return t;
}
//常规
int modexp(int a,int b,int n)
{
    int t=1;
    for(int i=0;i<b;i++)t=t*a;
    return t%n;
}

int main(void)
{
    int a=0,b=0,n=0;
    std::cin>>a>>b>>n;
    std::cout<<modExp(a,b,n)<<std::endl;
    std::cout<<modexp(a,b,n)<<std::endl;
    return 0;
}
谁能�l�我讲讲它这个方法是什么数学原理呢?
//�W�二个函��C��为测试正��性设�|?不考虑溢出问题

AIBPXTSHMF 2007-06-03 22:38 发表评论

Least Common Mutiple

AIBPXTSHMF — Sun, 03 Jun 2007 03:44:00 GMT

//非递归辗�{盔R��求最大公�U�数
int gcd(int a,int b)
{
    int r=0;
    r=a%b;
    while(r)
    {
        a=b;
        b=r;
        r=a%b;
    }
    return b;
}
//最��公倍数
int lcm(int a,int b)
{
    return (a*b)?a*b/gcd(a,b):0;
}

AIBPXTSHMF 2007-06-03 11:44 发表评论

Greatest Common Divisor

AIBPXTSHMF — Sat, 02 Jun 2007 11:59:00 GMT
辗�{盔R��递归��法:

//求最大公�U�数,公式if(a=b*q+r)then(gcd(a,b)=gcd(b,r))
int gcd(int a,int b)
{
    return (a%b)?gcd(b,a%b):b;
}
非递归��法:

//非递归辗�{盔R��
int gcd(int a,int b)
{
    int r=0;
    r=a%b;
    while(r)
    {
        a=b;
        b=r;
        r=a%b;
    }
    return b;
}

AIBPXTSHMF 2007-06-02 19:59 发表评论

mergesort优化若干证明

AIBPXTSHMF — Mon, 29 Jan 2007 08:52:00 GMT
     合�ƈ排序的runningtime是O(nlgn),插入排序为O(n*n),当合�q�排序的划分��C��定程度时可以应用插入排序。此时插入排序比合�ƈ排序的效率高,所以对合�ƈ排序做个修改�Q�n/k 长度为k的子序列用插入法排序。（要确定k的��|��

a.证明最坏情况下�Q�n/k个子序列用插入来排序的时间时O(nk).
   插入排序为O(n*n)�Q�那么对长度为k的子序列排序为O(k*k),n/k个子序列排序旉��和是(n/k)*O(k*k)=O(n*k),得证

b.证明在最坏情况下各子序列可以在O(nlg(n/k))下合�q?

c.设修改后合�ƈ��法的时间阶为O(nk+nlg(n/k)).��L��出最大渐�q�值k�Q�以O记号�Q�k是n的函敎ͼ�使得修改后的��法有和标准合�ƈ��法一��L��渐近�q�行旉��

d.k的值在实际中如何确定？

AIBPXTSHMF 2007-01-29 16:52 发表评论

MERGESORT

AIBPXTSHMF — Mon, 29 Jan 2007 02:25:00 GMT

自己错的�E�序mergesort攑֜�各个论坛上寻求答案，�l�果三天没�h回复。想来也是高手无暇，菜鸟无语。于是自己静下心来，仔细看了一下，�q�是标号弄错了。既然开了两个数�l�，那么数据拯��q�去后，标号应该是当前数�l�的�Q�结果用了原来数�l�的标号�Q�导致错误。这是修改后的源码：

// mergesort
#include < iostream >
using namespace std;

int merge( int A[], int p, int q, int r) {
int n1 = q - p + 1 ;
int n2 = r - q;
int * L = new int [n1];
int * R = new int [n2];
for ( int i = 0 ;i < n1; ++ i)
  L[i] = A[p + i];
for ( int j = 0 ;j < n2; ++ j)
  R[j] = A[q + 1 + j];
i = 0 ;j = 0 ;
int k = p;
while (i < n1 && j < n2) {
   if (L[i] <= R[j]) {A[k ++ ] = L[i ++ ];}
   else {A[k ++ ] = R[j ++ ];}
}
while (i < n1) {
  A[k ++ ] = L[i ++ ];}
while (j < n2) {
  A[k ++ ] = R[j ++ ];}
return ( 0 );
}

int mergesort( int A[], int p, int r) {
int q;
if (p < r) {
  q = (p + r) / 2 ;
  mergesort(A,p,q);
  mergesort(A,q + 1 ,r);
  merge(A,p,q,r);
}
return ( 0 );
}

int main() {
     int b[ 6 ] = { 11 , 65 , 53 , 78 , 38 , 63 } ;
    mergesort(b, 0 , 5 );
for ( int i = 0 ;i < 6 ; ++ i)
  cout << b[i] << ' \t ' ;
return ( 0 );
}

��小的错误，找了我半�?/p>

AIBPXTSHMF 2007-01-29 10:25 发表评论

Divide and Conquer

AIBPXTSHMF — Thu, 25 Jan 2007 12:16:00 GMT

     分治法，��֐�思义�Q�切分然后治理，�ȝ��是各个解决问题然后合�ƈ整理。递归的解军_��成n个较��规模的子问题，然后��各个结果合�q�从而解军_��来的问题�?br />DIVIDE�Q�将问题分解成一�p�d��子问题�?br />CONQUER�Q�递归地解军_��个子问题�Q�若问题��_��，则直接解冟�?br />COMBINE�Q�将子问题的�l�果合�ƈ成原问题的解�?br />自己�~�的代码�Q�结果又�q�行不�v来：ps:几经修改�Q�看来细节问题要注意�Q�简化推理是个好办法
//mergesort
#include
using namespace std;

int merge(int*A,int p,int q,int r){
int n1=q-p+1;
int n2=r-q;
int* L = new int[n1];
int* R = new int[n2];
for(int i=0;i L[i]=A[p+i];
for(int j=0;j R[j]=A[q+1+j];
i=0;j=0;
for(int k=p;k if(L[i]<=R[j]){A[k]=L[i++];}
else {A[k]=R[j++];}
}
return(0);
}

int mergesort(int*A,int p,int r){
int q;
if(p q=(p+r)/2;
mergesort(A,p,q);
mergesort(A,q+1,r);
merge(A,p,q,r);
}
return(0);
}

int main(){
    int b[6]={11,65,53,78,38,63};
    mergesort(b,0,5);
for(int i=0;i<6;++i)
cout< return(0);
}

以下引用自：gooler的专�?a >http://blog.csdn.net/Gooler/archive/2006/03/22/632422.aspx有各�U�排序算法quicksort,heapsort...
/*
* A is an array and p, q, and r are indices numbering elements of the array
* such that p <= q < r.
*
* This procedure assumes that the subarrays A[p. .q] and A[q + 1. .r] are in
* sorted order. It merges them to form a single sorted subarray that replaces
* the current subarray A[p. .r].
*/
void merge(int A[], int p, int q, int r) {
    int i, j, k, size;
    int* B;

    size = r - p + 1;

    B = new int[size]; /* temp arry for storing the merge result */

    /* initialize B */
    for (i = 0; i < size; ++i) {
        B[i] = 0;
    }

    i = p;
    j = q + 1;
    k = 0;

    /* compare and copy the smaller to B */
    while (i <= q && j <= r) {
        if (A[i] < A[j]) {
            B[k++] = A[i++];
        } else {
            B[k++] = A[j++];
        }
    }

    /* copy the rest to B */
    while (i <= q) {
        B[k++] = A[i++];
    }
    while (j <= r) {
        B[k++] = A[j++];
    }

    /* replace A[p..r] with B[0..r-p] */
    for (i = p, k = 0; i <= r; ++i, ++k) {
        A[i] = B[k];
    }

    delete[] B;
}

/*
* This procedure sorts the elements in the subarray A[p. .r].
*
* If p >= r, the subarray has at most one element and is therefore
* already sorted. Otherwise, the divide step simply computes an index
* q that partitions A[p. .r] into two subarrays: A[p. .q], containing n/2
* elements, and A[q + 1. .r], containing n/2 elements.
*/
void mergeSort(int A[], int p, int r) {
    if (p >= r) return;

    int q = (p + r) / 2;

    mergeSort(A, p, q);
    mergeSort(A, q + 1, r);
    merge(A, p, q, r);
}

AIBPXTSHMF 2007-01-25 20:16 发表评论

INSERT-SORT

AIBPXTSHMF — Wed, 24 Jan 2007 14:10:00 GMT
排序选择何种��法取决于排序元素个数及已排序的�E�度以及所使用的存储设�?br /> A[1..n]含n个元素的数组个数n=length[A]
插入排序�Q�－适合��量元素的排�?br />   for j<-- 2 to length[A]
       do key<--A[j]
         //��A[j]插入到排好序的序列A[1..j-1]
          i<--j-1
         while i>0 and A[i]>key
            do A[i+1]<--A[i]
            i<-- i-1
         A[i-1]<--key

用c++源程序描�q�ͼ�
#include
using namespace std;
int insertSort(int*array){
int key,i;
for(int j=1;j<6;++j){
     key=array[j]; //��第二个开始的元素攑օ�key
      i=j-1;
      while(i>=0&&array[i]>key){     //��大于key的元素至key原本所在位�|�的所有元素向后移动一个，�q�覆盖了key原来的位�|?br />           array[i+1]=array[i];
                   --i;
                                           }
       array[i+1]=key;//��key插入到array[i]的位�|?br />                            }
return(0);

}

int main(){
int a[6]={11,65,53,78,38,63};
insertSort(a);
for(int i=0;i<6;++i)
cout<return(0);
}

该方法在��法设计中叫增量�Ҏ��Incremental



AIBPXTSHMF 2007-01-24 22:10 发表评论

久久免费少妇高潮久久精品99,在线亚洲自拍,久久久久女教师免费一区

CodeGuru代码阅读(一)

Euclid扩展���法

Least Common Mutiple

Greatest Common Divisor

mergesort优化若干证明

MERGESORT

Divide and Conquer

INSERT-SORT

Euclid扩展��法