新建網(wǎng)頁 1
從歐拉角轉(zhuǎn)換到四元數(shù)
為了將角位移從歐拉角轉(zhuǎn)換到四元數(shù),可以使用從歐拉角構(gòu)造矩陣類似的方法。先將這三個旋轉(zhuǎn)分別轉(zhuǎn)換為四元數(shù),這是一個簡單的運算。再將這三個四元數(shù)連接成一個四元數(shù)。和矩陣一樣,有兩種情況需要考慮,第一種是慣性 -- 物體四元數(shù),第二種是物體-- 慣性四元數(shù)。因為它們互為共軛關(guān)系,所以我們只推導(dǎo)慣性--物體四元數(shù)。
設(shè)歐拉角為變量h、p、b,設(shè)h、p、b分別繞軸y、x、z旋轉(zhuǎn)的四元數(shù)。記住,使用負(fù)旋轉(zhuǎn)量,因為它們指定坐標(biāo)系中的旋轉(zhuǎn)角度。
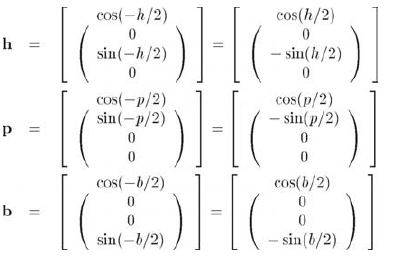
用正確的順序連接它們得到公式10.24:
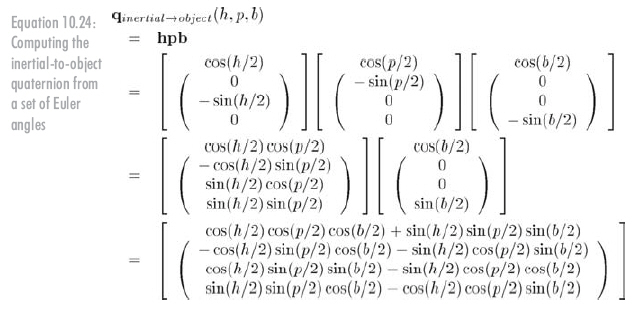
(記住,四元數(shù)乘法定義是按旋轉(zhuǎn)的順序從左向右乘。)
物體--慣性四元數(shù)是慣性--物體四元數(shù)的共軛,見公式10.25:
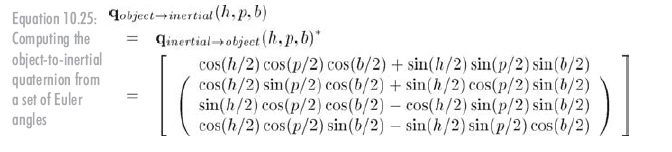
從四元數(shù)轉(zhuǎn)換到歐拉角
根據(jù)前面的公式發(fā)現(xiàn):


現(xiàn)在可以將它直接轉(zhuǎn)換到代碼中,如程序清單10.5所示,它能把慣性--物體四元數(shù)轉(zhuǎn)換成歐拉角。
Listing 10.5: Converting an inertial-to-object quaternion to Euler angles
// Use global variables for input and output
float w,x,y,z;
float h,p,b;
// Extract sin(pitch)
float sp = –2.0f * (y*z + w*x);
// Check for Gimbal lock, giving slight tolerance for numerical imprecision
if (fabs(sp) > 0.9999f) {
// Looking straight up or down
p = 1.570796f * sp; // pi/2
// Compute heading, slam bank to zero
h = atan2(–x*z – w*y, 0.5f – y*y – z*z);
b = 0.0f;
} else {
// Compute angles
p = asin(sp);
h = atan2(x*z – w*y, 0.5f – x*x – y*y);
b = atan2(x*y – w*z, 0.5f – x*x – z*z);
}
將物體--慣性四元數(shù)轉(zhuǎn)換到歐拉角,所用的代碼和上面非常類似。只是將x
、y
、z
值變負(fù),因為物體--慣性四元數(shù)是慣性--物體四元數(shù)的共軛。
Listing 10.6: Converting an object-to-inertial quaternion to Euler angles
// Extract sin(pitch)
float sp = –2.0f * (y*z – w*x);
// Check for Gimbal lock, giving slight tolerance for numerical imprecision
if (fabs(sp) > 0.9999f) {
// Looking straight up or down
p = 1.570796f * sp; // pi/2
// Compute heading, slam bank to zero
h = atan2(–x*z + w*y, 0.5f – y*y – z*z);
b = 0.0f;
} else {
// Compute angles
p = asin(sp);
h = atan2(x*z + w*y, 0.5f – x*x – y*y);
b = atan2(x*y + w*z, 0.5f – x*x – z*z);
}