新建網(wǎng)頁 1
我們使用D3DXMatrixLookAtLH函數(shù)來計(jì)算視圖空間變換矩陣。這個(gè)函數(shù)對(duì)于在固定位置布置和對(duì)準(zhǔn)攝像機(jī)是非常好用的，不過它的用戶接口對(duì)于要響應(yīng)用戶輸入來實(shí)現(xiàn)攝像機(jī)移動(dòng)就不那么好用了。這就激發(fā)我們用我們自己的方法來解決，這里我們展示了怎樣實(shí)現(xiàn)一個(gè)Camera類，它使我們能夠比D3DXMatrixLookAtLH函數(shù)更好地操作攝像機(jī)，并且可以用來作為飛行模擬攝像機(jī)和第一人稱視角攝像機(jī)。
12.1攝像機(jī)設(shè)計(jì)
我們定義一個(gè)相對(duì)于世界坐標(biāo)系的位置和攝像機(jī)的方向，這里使用四個(gè)攝像機(jī)向量：right vector , up vector,look vector 以及 position vector,如圖12.1所示。這些向量用來為攝像機(jī)定義一個(gè)坐標(biāo)系來描述在世界坐標(biāo)中的對(duì)應(yīng)關(guān)系。因?yàn)?span lang="EN-US"> right ，
up 和
look 向量定義了攝像機(jī)在世界中的方向，我們有時(shí)把它們?nèi)齻€(gè)向量一起稱為方向向量（
orientation vectors）。方向向量必須被標(biāo)準(zhǔn)化。假如彼此互相垂直且都是單位長度，那么我們就稱它們是正交標(biāo)準(zhǔn)化向量。我們做這些限制是因?yàn)榈纫粫?huì)兒我們要將方向向量插入到一個(gè)行矩陣中。因?yàn)樾邢蛄渴钦粯?biāo)準(zhǔn)化的，所以該矩陣也就是正交矩陣。回憶一下，正交矩陣有一個(gè)特性就是它的逆矩陣等于它的轉(zhuǎn)置矩陣。
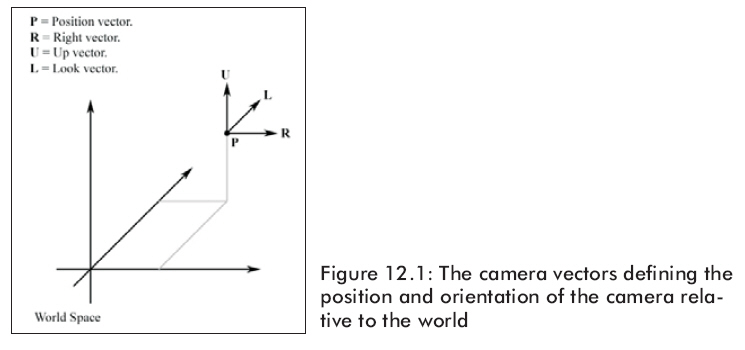
有了這四個(gè)向量來描述攝像機(jī)，我們的攝像機(jī)就能夠按照下面六種方式變化了：
圍繞right向量旋轉(zhuǎn)（pitch傾斜）
圍繞up向量旋轉(zhuǎn)（yaw偏航）
圍繞look向量旋轉(zhuǎn)（roll滾轉(zhuǎn)）
沿著right向量平移（strafe）
沿著up向量飛行（fly）
沿著look向量移動(dòng)（move）
通過這六種操作，我們能夠沿著三個(gè)軸移動(dòng)以及饒著三個(gè)軸旋轉(zhuǎn)，這給了我們一個(gè)六度的自由。下面的Camera類定義了我們要的描述數(shù)據(jù)以及想要的方法：
enum eCameraType { LAND_OBJECT, AIR_CRAFT };
class cCamera
{
private:
eCameraType m_camera_type;
D3DXVECTOR3 m_right;
D3DXVECTOR3 m_up;
D3DXVECTOR3 m_look;
public:
D3DXVECTOR3 m_pos;
public:
cCamera();
cCamera(eCameraType camera_type);
~cCamera() { };
void strafe(float units); // left/right
void fly(float units); // up/down
void walk(float units); // forward/backward
void pitch(float angle); // rotate on right vector
void yaw(float angle); // rotate on up vector
void roll(float angle); // rotate on look vector
void get_view_matrix(D3DXMATRIX* v);
void set_camera_type(eCameraType camera_type);
void get_right(D3DXVECTOR3* right);
void get_up(D3DXVECTOR3* up);
void get_look(D3DXVECTOR3* look);
};
在類中我們定義了一個(gè)還沒有討論的eCameraType枚舉類型。目前，我們的攝像機(jī)支持兩種攝像機(jī)模式，LANDO_BJECT模式和AIR_CRAFT模式。AIR_CRAFT模式允許我們?cè)诳臻g中完全自由的移動(dòng)。不過，在有些游戲中，比如第一人稱設(shè)計(jì)游戲，人是不能飛的；因此我們必須限制它在某些軸上的運(yùn)動(dòng)。指定為LAND_OBJECT模式的攝像機(jī)就限制了這些。
12.2 實(shí)現(xiàn)細(xì)節(jié)
12.2.1計(jì)算視圖矩陣
我們現(xiàn)在演示怎樣根據(jù)攝像機(jī)向量來計(jì)算視圖矩陣變換的。讓 p = (px,py,pz),r = (rx,ry,rz),u = (ux,uy,uz)以及 d = (dx,dy,dz)分別表示 position, right, up 以及 look 向量。
視圖空間變換是指在世界坐標(biāo)系中進(jìn)行幾何變換以便將照相機(jī)平移變換到坐標(biāo)系的原點(diǎn)并把它的方向旋轉(zhuǎn)至朝向Z軸的正方向（如圖12.2）。
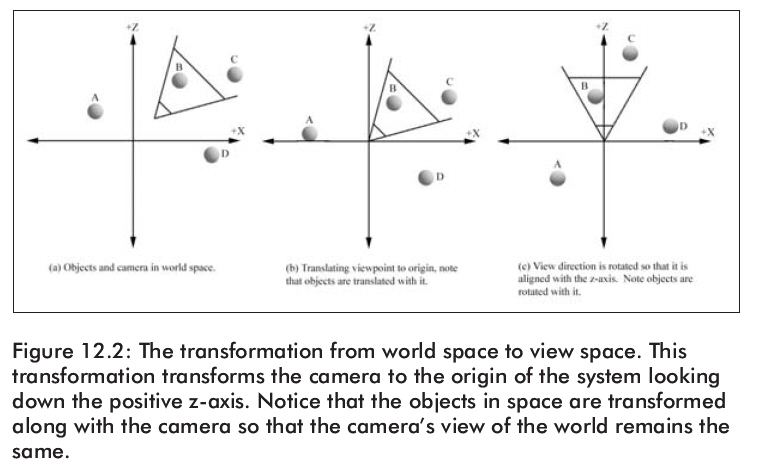
因此，我們希望有一個(gè)象這樣的變換矩陣V：
pV = (0, 0, 0)—矩陣V能將攝像機(jī)移動(dòng)到原點(diǎn)。
rV = (1, 0, 0)—矩陣V能將攝像機(jī)的right向量與世界坐標(biāo)系中的x軸對(duì)齊。
uV = (0, 1, 0)—矩陣V能將攝像機(jī)的up向量與世界坐標(biāo)系中的y軸對(duì)齊。
dV = (0, 0, 1)—矩陣V能將攝像機(jī)的look向量與世界坐標(biāo)系中的z軸對(duì)齊。
我們能將變換任務(wù)分為兩個(gè)部分：1）平移部分，將攝像機(jī)的位置移動(dòng)到原點(diǎn)；2）旋轉(zhuǎn)部分，將攝像機(jī)的方向向量與世界坐標(biāo)系的軸對(duì)齊。
12.2.1.1 第一部分：平移
平移只需要利用 –p就可簡(jiǎn)單地將 p 移動(dòng)到原點(diǎn)，因?yàn)?p–p=0。因此我們能夠用下面的矩陣來描述視圖變換中的平移部分：
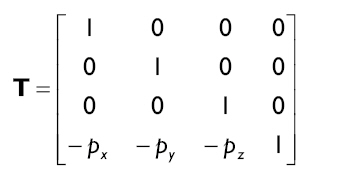
12.2.1.2 第二部分：旋轉(zhuǎn)
矯正攝像機(jī)的三個(gè)方向向量使其與世界坐標(biāo)系的軸對(duì)齊需要更多的工作。我們需要一個(gè)3*3的旋轉(zhuǎn)矩陣A，它能將right，up和look分別與x-，y-以及z軸對(duì)齊。這個(gè)矩陣將滿足如下三個(gè)等式：
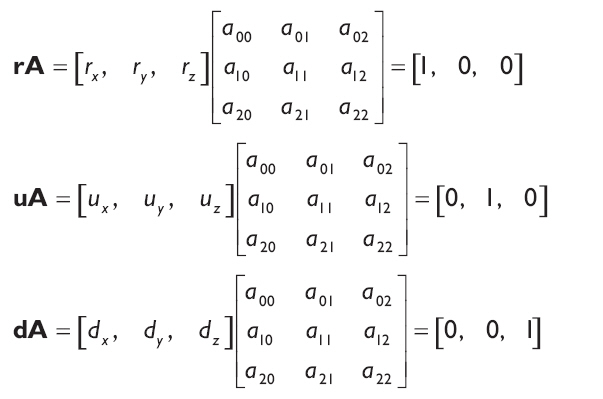
注意：我們?cè)谶@里使用3*3矩陣來工作是因?yàn)楝F(xiàn)在不需要額外的信息來表現(xiàn)旋轉(zhuǎn)。等一下我們將它增加到常用的4*4矩陣。
因?yàn)檫@三個(gè)等式都有一個(gè)相同系數(shù)矩陣A ，所以我們能夠把它們合在一起。我們把它們從新寫到一起來：
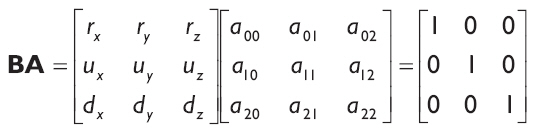
求A有很多方法，但是我們知道A是B逆矩陣因?yàn)?strong>BA = BB-1 = I。因?yàn)?span lang="EN-US">B 是一個(gè)正交矩陣（它的行向量是正交標(biāo)準(zhǔn)化的），我們知道它的逆矩陣就是它的轉(zhuǎn)置矩陣。因此，將方向向量和世界坐標(biāo)系中的坐標(biāo)軸對(duì)齊的變換如下：
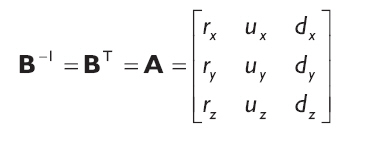
12.2.1.3 將兩部分合并
最后，將A增加為4*4矩陣，同時(shí)將平移部分合并到旋轉(zhuǎn)部分形成的視圖變換矩陣V：
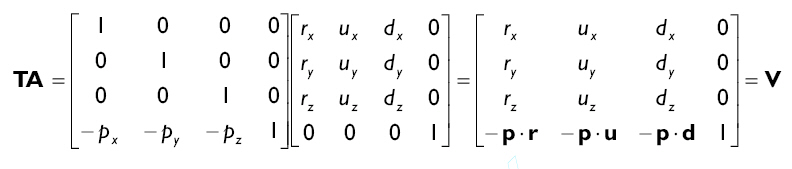
我們?cè)?span lang="EN-US">cCamera::get_view_matrix方法中建立這個(gè)矩陣：
void cCamera::get_view_matrix(D3DXMATRIX* v)
{
// keep camera's axis orthogonal to each other
D3DXVec3Normalize(&m_look, &m_look);
D3DXVec3Cross(&m_up, &m_look, &m_right);
D3DXVec3Normalize(&m_up, &m_up);
D3DXVec3Cross(&m_right, &m_up, &m_look);
D3DXVec3Normalize(&m_right, &m_right);
// build the view matrix
float x = -D3DXVec3Dot(&m_right, &m_pos);
float y = -D3DXVec3Dot(&m_up, &m_pos);
float z = -D3DXVec3Dot(&m_look, &m_pos);
(*v)(0, 0) = m_right.x; (*v)(0, 1) = m_up.x; (*v)(0, 2) = m_look.x; (*v)(0, 3) = 0.0f;
(*v)(1, 0) = m_right.y; (*v)(1, 1) = m_up.y; (*v)(1, 2) = m_look.y; (*v)(1, 3) = 0.0f;
(*v)(2, 0) = m_right.z; (*v)(2, 1) = m_up.z; (*v)(2, 2) = m_look.z; (*v)(2, 3) = 0.0f;
(*v)(3, 0) = x; (*v)(3, 1) = y; (*v)(3, 2) = z; (*v)(3, 3) = 1.0f;
}
你可能想知道方法中前面幾行代碼是干什么的。在幾次旋轉(zhuǎn)后，攝像機(jī)的方向向量可能變的不相互垂直了。因此，每當(dāng)該函數(shù)被調(diào)用時(shí)，我們根據(jù)look向量重新計(jì)算up和right向量，使它們保持相互垂直。新的up向量是這樣計(jì)算的up = look × right。 接著新的right向量是這樣計(jì)算的right = up × look