繪制流水線(2)
2.3 渲染管線
一旦我們描述幾何學(xué)上的3D場(chǎng)景和設(shè)置了虛擬照相機(jī),我們要把這個(gè)場(chǎng)景轉(zhuǎn)換成2D圖象顯示在顯示器上。這一系列必須完成的操作就叫做渲染管線。圖2.7展示了一個(gè)簡(jiǎn)化的渲染管線,隨后將詳細(xì)解釋圖中的每一部分。
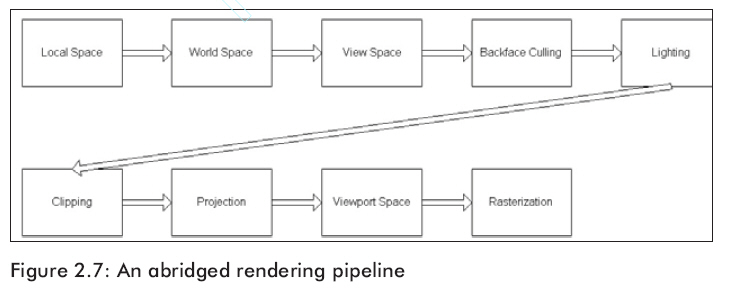
渲染管線中的許多級(jí)都是從一個(gè)坐標(biāo)系到另一個(gè)坐標(biāo)的幾何變換。這些變換都通過(guò)矩陣變換來(lái)實(shí)現(xiàn)。Direct3D為我們進(jìn)行變換計(jì)算并且如果顯卡支持硬件變換的話那就更有利了。使用Direct3D進(jìn)行矩陣變換,我們唯一要做的事就是提供從一個(gè)系統(tǒng)變換到另一個(gè)系統(tǒng)的變換矩陣就可以了。我們使用IDirect3DDevice9::SetTranform方法提供變換矩陣。它輸入一個(gè)表示變換類型的參數(shù)和一個(gè)變換矩陣。如圖2.7所示,為了進(jìn)行一個(gè)從自身坐標(biāo)系到世界坐標(biāo)系的變換,我們可以這樣寫:
|
Device->SetTransform(D3DTS_WORLD, &worldMatrix); |
2.3.1自身坐標(biāo)系(Local Space)
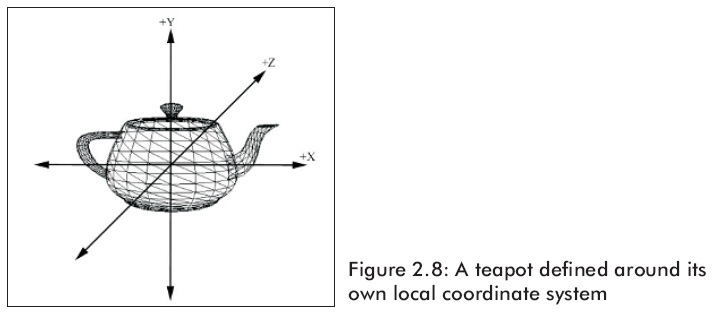
自身坐標(biāo)系又叫做建模空間,這是我們定義物體的三角形列的坐標(biāo)系。自身坐標(biāo)系簡(jiǎn)化了建模的過(guò)程。在物體自己的坐標(biāo)系中建模比在世界坐標(biāo)系中直接建模更容易。例如,在自身坐標(biāo)系中建模不像在世界坐標(biāo)系中要考慮本物體相對(duì)于其他物體的位置、大小、方向關(guān)系。圖 2.8所示是一個(gè)在自身局部坐標(biāo)系中定義的茶壺。
2.3.2世界坐標(biāo)系(World Space)
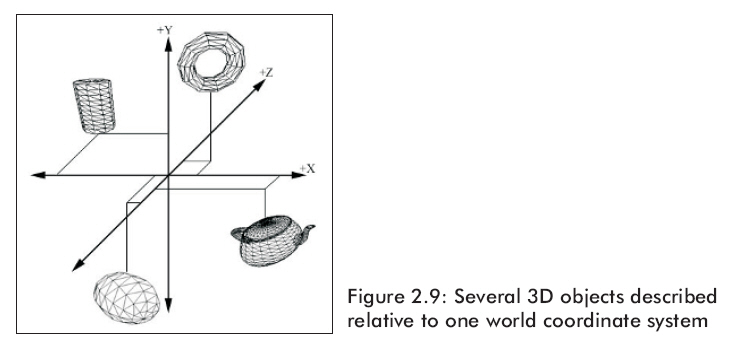
一旦我們構(gòu)造了各種模型,它們都在自己的自身坐標(biāo)系中,但是我們需要把它們都放到同一個(gè)世界坐標(biāo)系中。物體從自身坐標(biāo)系到世界坐標(biāo)系中的變換叫做世界變換。世界變換通常是用平移、旋轉(zhuǎn)、縮放操作來(lái)設(shè)置模型在世界坐標(biāo)系中的位置、大小、方向。世界變換就是通過(guò)各物體在世界坐標(biāo)系中的位置、大小和方向等相互之間的關(guān)系來(lái)建立所有物體。圖2.9所示是相對(duì)于世界坐標(biāo)系描述的幾個(gè)3D物體。
世界變換由一個(gè)矩陣表示,并且在Direct3D中調(diào)用IDirect3DDevice9::SetTransform方法設(shè)置它,記住將轉(zhuǎn)換類型設(shè)為D3DTS_WORLD。例如我們要在世界坐標(biāo)系中放置一個(gè)立方體定位在(-3,2,6)和一個(gè)球體定位在(5,0,-2),我們可以這樣寫程序:
|
//創(chuàng)建立方體的世界矩陣(一個(gè)平移矩陣) D3DXMATRIX cubeWorldMatrix; D3DXMatrixTranslation(&cubeWorldMatrix, -3.0f, 2.0f, 6.0f); //創(chuàng)建球體的世界矩陣(一個(gè)平移矩陣) D3DXMATRIX sphereWorldMatrix; D3DXMatrixTranslation(&sphereWorldMatrix, 5.0f, 0.0f, -2.0f); // 變換立方體,然后繪制它 Device->SetTransform(D3DTS_WORLD, &cubeWorldMatrix); drawCube(); // draw the cube // 因?yàn)榍蝮w使用一個(gè)不同的世界變換,我們必須更改世界矩陣為球體的, // 如果不更改,球體將繪制在上一個(gè)世界矩陣的位置上(立方體的世界矩陣) Device->SetTransform(D3DTS_WORLD, &sphereWorldMatrix); drawSphere(); // 繪制球體 |
這是個(gè)非常簡(jiǎn)單的實(shí)例,沒有用到矩陣的旋轉(zhuǎn)和縮放。但是一般很多物體都需要進(jìn)行這些變換,不過(guò)這個(gè)例子也還是展示了世界變換是怎樣進(jìn)行的。
2.3.3視圖坐標(biāo)系(View Space)
世界坐標(biāo)系中的幾何圖與照相機(jī)是相對(duì)于世界坐標(biāo)系而定義的,如圖2.10所示。然而在世界坐標(biāo)系中當(dāng)照相機(jī)是任意放置和定向時(shí),投影和其它一些操作會(huì)變得困難或低效。為了使事情變得更簡(jiǎn)單,我們將照相機(jī)平移變換到世界坐標(biāo)系的原點(diǎn)并把它的方向旋轉(zhuǎn)至朝向Z軸的正方向,當(dāng)然,世界坐標(biāo)系中的所有物體都將隨著照相機(jī)的變換而做相同的變換。這個(gè)變換就叫做視圖坐標(biāo)系變換(view space transformation)。

視圖坐標(biāo)的變換矩陣可以通過(guò)如下的D3DX函數(shù)計(jì)算得到:
|
D3DXMATRIX *D3DXMatrixLookAtLH( D3DXMATRIX* pOut, // 指向返回的視圖矩陣 CONST D3DXVECTOR3* pEye, // 照相機(jī)在世界坐標(biāo)系的位置 CONST D3DXVECTOR3* pAt, // 照相機(jī)在世界坐標(biāo)系的目標(biāo)點(diǎn) CONST D3DXVECTOR3* pUp // 世界坐標(biāo)系的上方向(0, 1, 0) ); |
pEye參數(shù)指定照相機(jī)在世界坐標(biāo)系中的位置,pAt參數(shù)指定照相機(jī)所觀察的世界坐標(biāo)系中的一個(gè)目標(biāo)點(diǎn),pUp參數(shù)指定3D世界中的上方向,通常設(shè)Y軸正方向?yàn)樯戏较颍慈≈禐椋?,1,0)。
例如:假設(shè)我們要把照相機(jī)放在點(diǎn)(5,3,-10),并且目標(biāo)點(diǎn)為世界坐標(biāo)系的中點(diǎn)(0,0,0),我們可以這樣獲得視圖坐標(biāo)系變換矩陣:
|
D3DXVECTOR3 position(5.0f, 3.0f, –10.0f); D3DXVECTOR3 targetPoint(0.0f, 0.0f, 0.0f); D3DXVECTOR3 worldUp(0.0f, 1.0f, 0.0f);
D3DXMATRIX V; D3DXMatrixLookAtLH(&V, &position, &targetPoint, &worldUp); |
視圖坐標(biāo)系變換也是通過(guò)IDirect3DDevice9::SetTransform來(lái)實(shí)現(xiàn)的,只是要將變換類型設(shè)為D3DTS_VIEW,如下所示:
|
Device->SetTransform(D3DTS_VIEW, &V); |
2.3.4背面消除(Backface Culling)
一個(gè)多邊形有兩個(gè)表面,我們將一個(gè)標(biāo)為正面,一個(gè)為背面。通常,后表面總是不可見的,這是因?yàn)閳?chǎng)景中大多數(shù)物體是密封的。例如盒子、圓柱體、箱子、角色等,并且我們也不能把照相機(jī)放入物體的內(nèi)部。因此照相機(jī)永不可能看到多邊形的背面。這是很重要的,如果我們能看背面,那么背面揀選就不可能工作。
圖2.11表示了一個(gè)物體在視圖坐標(biāo)系中的正面。一個(gè)多邊形的邊都是面向照相機(jī)叫正面多邊形,而一個(gè)多邊形的邊都背對(duì)照相機(jī)叫背面多邊形。
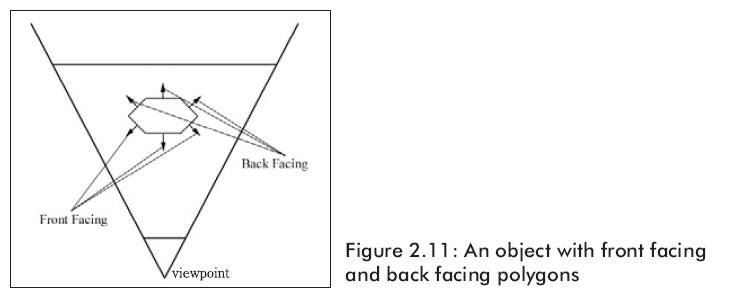
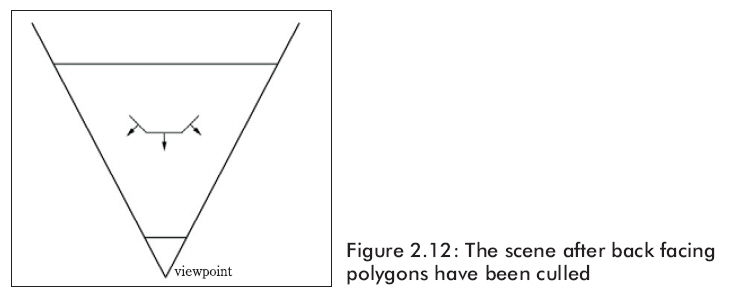
由圖2.11可知,正面多邊形擋住了在它后面的背面多邊形,Direct3D將通過(guò)消除(即刪除多余的處理過(guò)程)背面多邊形來(lái)提高效率,這種方法就叫背面揀選。圖2.12展示了背面揀選之后的多邊形,從照相機(jī)的觀察點(diǎn)來(lái)看,仍將繪制相同的場(chǎng)景到后備表面,那些被遮住的部分無(wú)論如何都永遠(yuǎn)不會(huì)被看見的。
當(dāng)然,為了完成這項(xiàng)工作,Direct3D需要知道哪個(gè)多邊形是正面,哪個(gè)是背面。Direct3D中默認(rèn)頂點(diǎn)以順時(shí)針?lè)较颍ㄔ谟^察坐標(biāo)系中)形成的三角形為正面,以逆時(shí)針?lè)较蛐纬傻娜切螢楸趁妗?/p>
如果我們不想使用默認(rèn)繪制狀態(tài),我們可以通過(guò)改變D3DRS_CULLMODE來(lái)改變渲染狀態(tài):
|
Device->SetRenderState(D3DRS_CULLMODE, Value); |
Value可以是如下一個(gè)值:
D3DCULL_NONE——完全不使用背面消除
D3DCULL_CW——消除順時(shí)針?lè)较颦h(huán)繞的三角形
D3DCULL_CCW——消除逆時(shí)針?lè)较颦h(huán)繞的三角形,這是默認(rèn)值。
posted on 2008-03-14 09:04 lovedday 閱讀(1052) 評(píng)論(0) 編輯 收藏 引用



