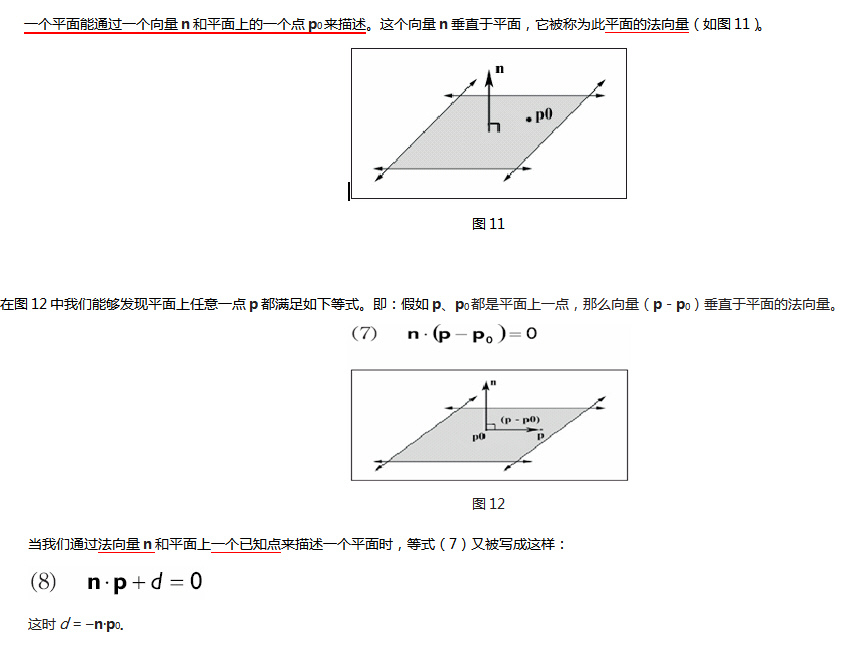
在代碼中描述一個平面:僅僅需要一個法向量n和常數d就可以了�����。因此我們就使用一個4D向量(我們記錄成(n,
d))來實現它���。D3DX庫中用如下的結構來定義一個平面:
對照等式(8)可知:這里a,
b和c是平面法向量n的成員�����,d就是那個常數�。
我們判定點和平面的關系主要是利用等式(8)來實現�。例如,假設平面(n,
d)�,我們能判定點p和平面的關系:
假如n·p
+
d
= 0�����,那么點p與平面共面。
假如n·p
+
d
>0,那么點p在平面的前面且在平面的正半空間里���。
假如n·p
+
d
<0,那么點p在平面的背面且在平面的負半空間里。
下邊的D3DX函數就是利用n·p
+
d
來判定點和平面的關系的函數:
FLOAT D3DXPlaneDotCoord(
CONST D3DXPLANE *pP,
//
平面
CONST D3DXVECTOR3 *pV
//
點
);
|
//
測試點相對于平面的位置
D3DXPLANE p(0.0f, 1.0f,
0.0f, 0.0f);
D3DXVECTOR3 v(3.0f, 5.0f,
2.0f);
float
x = D3DXPlaneDotCoord( &p, &v );
if(
x approximately equals 0.0f ) // v在平面.上
if(
x > 0 ) // v在正半空間
if(
x < 0 ) // v在負半空間
|
我們能通過兩種方法創建平面�。
第一種方法�����,直接用指定法線和點創建平面���。假設法線n和在平面上的已知點p0,我們就能求出d:
n·p0+
d = 0
n·p0
= -d
-n·p0
= d
D3DX庫提供如下函數來完成創建平面的任務:
|
D3DXPLANE *D3DXPlaneFromPointNormal(
D3DXPLANE* pOut,
// Result.
CONST D3DXVECTOR3*
pPoint, // Point on the plane.
CONST D3DXVECTOR3*
pNormal // The normal of the plane.
);
|
第二種方法���,我們能通過在平面上的3個點創立一個平面。
假如有點p0,
p1,
p2�,那么我們就能得到平面上的兩個向量:
因此我們能通過把平面上的兩個向量進行叉乘得到平面的法線�?��;貞涀笫肿鴺讼?。
n = u × v
Then, -(n ·
p0) = d.
D3DX庫提供如下函數來完成通過同一平面上的3個點確定一個平面:
|
D3DXPLANE *D3DXPlaneFromPoints(
D3DXPLANE* pOut,
// Result.
CONST D3DXVECTOR3*
pV1, // Point 1 on the plane.
CONST D3DXVECTOR3*
pV2, // Point 2 on the plane.
CONST D3DXVECTOR3*
pV3 // Point 3 on the plane.
);
|
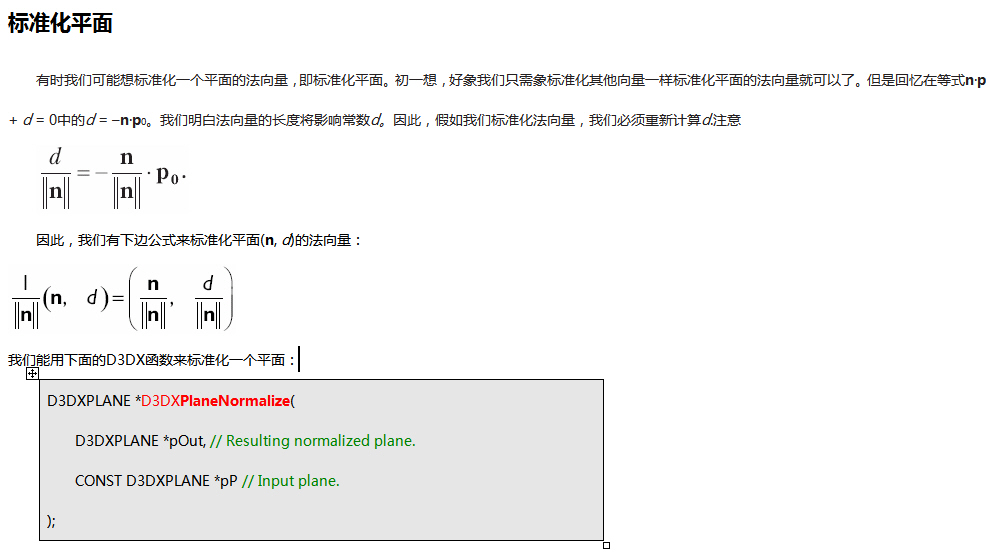
我們能夠通過如下處理來變換一個面(n,
d),就象一個4D向量通過乘以它所期望的變換矩陣的逆矩陣一樣來達到變換目的�����。注意平面的法向量必須首先被標準化�����。
我們能用下面的D3DX函數來完成操作:
|
D3DXPLANE *D3DXPlaneTransform(
D3DXPLANE *pOut,
// Result
CONST D3DXPLANE *pP,
// Input plane.
CONST D3DXMATRIX *pM
// Transformation matrix.
);
|
示例代碼:
|
D3DXMATRIX T(...);
// Init. T to a desired transformation.
D3DXMATRIX inverseOfT;
D3DXMATRIX
inverseTransposeOfT;
D3DXMatrixInverse( &inverseOfT,
0, &T );
D3DXMatrixTranspose( &inverseTransposeOfT,
&inverseOfT );
D3DXPLANE p(...);
// Init. Plane.
D3DXPlaneNormalize( &p, &p
); // make sure normal is normalized.
D3DXPlaneTransform( &p, &p,
&inverseTransposeOfT );
|
設想在游戲中的一個玩家�����,正用他的槍射擊敵人。我們怎么判斷子彈是否從一個位置擊中另一個位置的目標?一個方法是用一條射線模擬子彈,用一個球體模型模擬敵人。(球體模型只是一個球體,它緊緊的圍繞一個物體,從而粗略地表示它的大小���。球體模型將在第11章中做更詳細的介紹。)那么通過計算我們就能夠判定是否射中球體。在這部分我們學習射線的數學模型�。
一條射線能用一個起點和方向來描述���。射線的參數方程是:
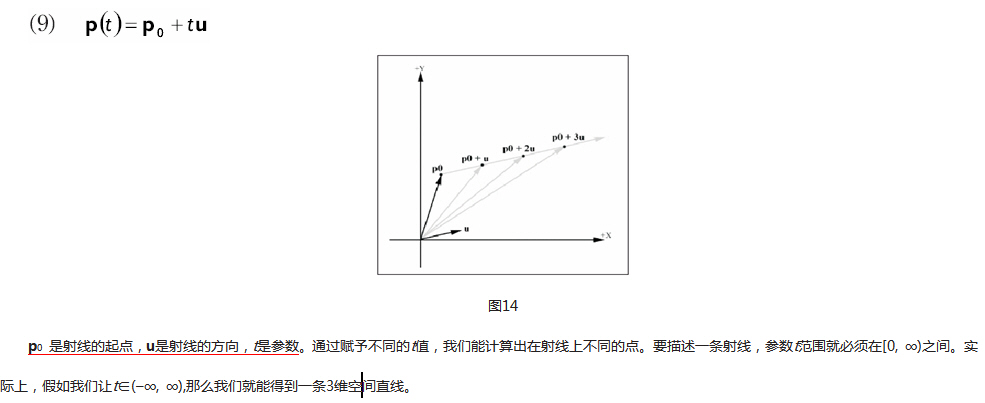
假設一條射線p(t)
= p0
+
tu
和 一個平面n·p
+
d
= 0�,我們想知道射線是否與平面相交�����,以及相交的交點信息(如果相交的話)。照這樣做���,我們把射線代入平面方程并且求滿足平面方程的參數t,解答出來的參數就是相交的點���。
把等式(9)代入平面方程:
