D3D編程必備的數學知識(4)
基本變換
當用Direct3D編程時,我們使用4×4矩陣來進行矩陣變換。用它的原因是:我們設置一個4×4矩陣X是為了更精確的描述矩陣變換。同樣我們設置一個相匹配的點或者把向量的分量放置到一個1×4的行矩陣V中。VX的乘積返回一個新的向量V’。例如:讓X沿著x軸平移10個單位同時V = [2, 6, –3, 1],乘積VX = V’= [12, 6, –3, 1]。
有一些東西需要闡明。我們使用4×4矩陣是因為這樣的大小能表現我們需要的所有變換。最初看來一個3×3的好象更適合3D。然而這里有很多種我們喜歡用的變換是不能用一個3×3的矩陣來表示的,比如平移、投影、反射。我們使用向量-矩陣相乘來工作,因此我們至少要通過一個矩陣乘法來完成相應的變化。增大到4×4的矩陣后,它允許我們用一個矩陣描述更多的變換,并且向量-矩陣乘法是可行的。
我們說過把一個相匹配的點或者一個向量的成員放置到一個1×4的行矩陣中。但是點和向量是3D的!為什么我們要用一個1×4的行矩陣呢?我們必需把3D點/向量增大為4D的單行矩陣,是為了符合向量與矩陣的乘法定義,而1×3的單行矩陣和4×4的矩陣相乘是不允許的。
那么,我們怎么使用第四個成員(我們用w來表示)呢?當我們把一個點放置到一個1×4的行矩陣中時,我們設置w為1。允許對點進行適當的平移。因為向量和位置無關,所以向量的平移沒有被定義,如果試圖這樣做會返回一個無意義的向量。為了防止對向量進行平移,當在把一個向量放置到一個1×4行矩陣中時我們把w設置為0。例如:
把點p = (p1, p2, p3)放置到一個單行矩陣中就象這樣:
[p1, p2, p3, 1],
同樣把向量v = (v1, v2, v3) 放置到一個單行矩陣中就象這樣:
[v1, v2, v3, 0]。
注意:我們設置w = 1是為了讓點可以被恰當的移動,同樣我們設置w = 0是為了防止向量被平移。當我們檢查矩陣實際平移時這是一個非常清晰的模型。
有時一個矩陣變換時我們改變向量成員w的值,即w≠0 且 w≠1。考慮下邊例子:

矩陣平移
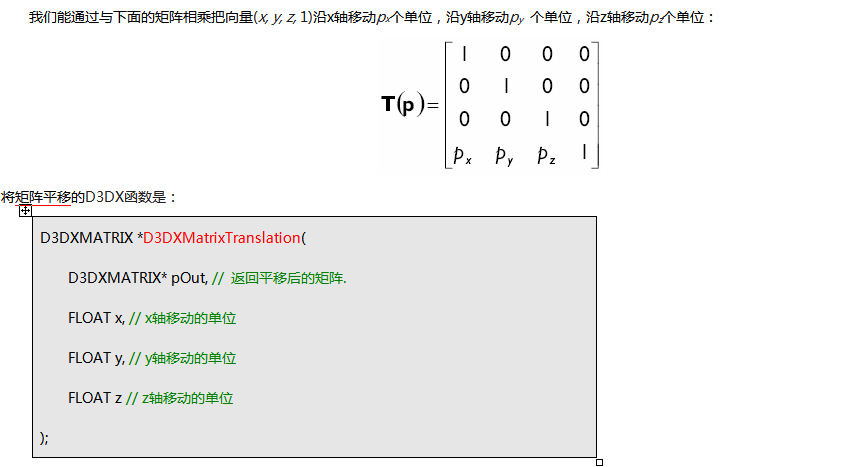
矩陣旋轉


旋轉矩陣R的逆矩陣等于它的轉置矩陣:RT= R-1。這樣的矩陣我們說它們是正交矩陣的。
矩陣縮放

綜合變換
常常我們要對一個向量進行一系列的變換。比如,我們可能先縮放一個向量,然后旋轉它,最后把它平移到指定的位置。
例如:先把向量p = [5, 0, 0, 1] 在所有軸上縮小為原來的1/5,然后沿著y軸旋轉π/4,最后把它在x軸上移動1個單位,在y軸上移動2個單位,在z軸上移動3個單位。
解答:注意我們必須完成縮放,沿y軸旋轉,以及移動。我們設縮放、旋轉、移動的變換矩陣分別是S, Ry, T,如下:

我們能用矩陣乘法把幾個變換矩陣轉換成一個矩陣,它是非常有益的矩陣。比如,重新考慮這部分開始的例子。通過使用矩陣相乘把3個變換矩陣合成一個矩陣。注意我們必須按實際應用的順序來進行矩陣相乘。
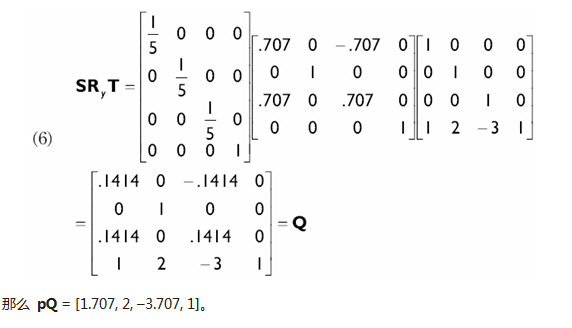
聯合變換有提高效率的能力。假如我們需要對一組數量巨大的向量(在3D圖形任務中是很普遍的)進行同樣的縮放,旋轉以及移動變換。替換這一系列的變換,即就象等式(5)中對每一個向量的做法,我們能把所有3個變換轉換到一個矩陣中,即就象在等式(6)中的做法。這樣我們只需要對每一個向量進行一次乘法就可以實現3種變換。這就減少了大量的向量-矩陣乘法操作。
一些向量變換函數
D3DX庫分別提供了下邊兩個對點和向量的變換函數。D3DXVec3TransformCoord函數變換點同時設置向量第4個成員為1(用于變換點向量)。D3DXVec3TransformNormal函數變換向量并且設置第4個成員為0(用于變換方向向量)。
D3DXVECTOR3 *D3DXVec3TransformCoord(
D3DXVECTOR3* pOut, // 返回的點向量
CONST D3DXVECTOR3* pV, // 點向量
CONST D3DXMATRIX* pM // 變換矩陣
);
|
D3DXMATRIX T(...); // 初始化矩陣 D3DXVECTOR3 p(...); // 初始化點 D3DXVec3TransformCoord( &p, &p, &T); // 變換一個點 |
D3DXVECTOR3 *WINAPI D3DXVec3TransformNormal(
D3DXVECTOR3 *pOut, //返回的方向向量
CONST D3DXVECTOR3 *pV, // 方向向量
CONST D3DXMATRIX *pM //變換矩陣
);
|
D3DXMATRIX T(...); // 初始化變換矩陣 D3DXVECTOR3 v(...); // 初始化方向向量 D3DXVec3TransformNormal( &v, &v, &T); // 變換方向向量 |
注意:D3DX庫也提供D3DXVec3TransformCoordArray和D3DXVec3TransformNormalArray來分別變換一個點數組和向量數組。



