幾何學中,我們用有向線段表示向量,如圖1。向量的兩個屬性是他的長度和他的頂點所指的方向。因此,可以用向量來模擬既有大小又有方向的物理模型。例如,以后我們要實現的粒子系統。我們用向量來模擬粒子的速度和加速度。在3D計算機圖形學中我們用向量不僅僅模擬方向。例如我們常常想知道光線的照射方向,以及在3D世界中的攝象機。向量為在3維空間中表示方向的提供了方便。
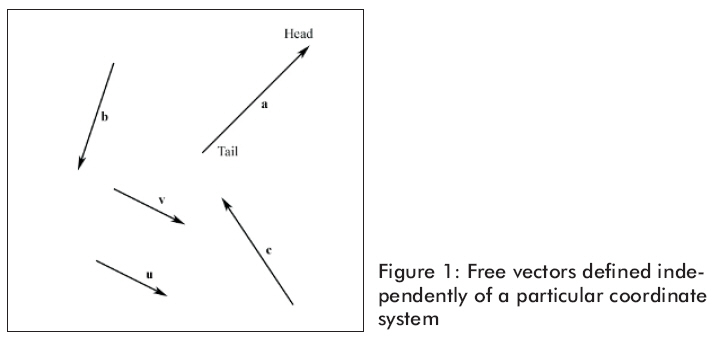
向量與位置無關。有同樣長度和方向的兩個向量是相等的,即使他們在不同的位置。觀察彼此平行的兩個向量,例如在圖1中u和v是相等的。
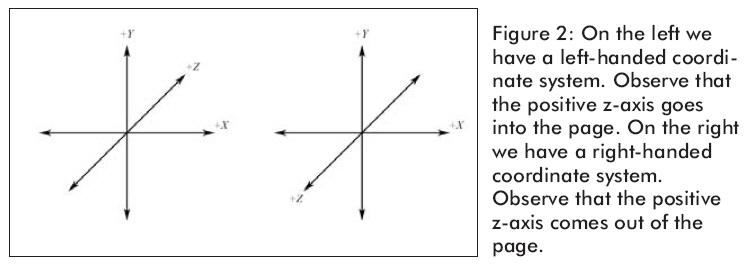
我們繼續學習左手坐標系。圖2顯示的是左手坐標系和右手坐標系。兩者不同的是Z軸的方向。在左手坐標系中Z軸是向書的里面去的,而右手坐標系是向書的外邊去的。
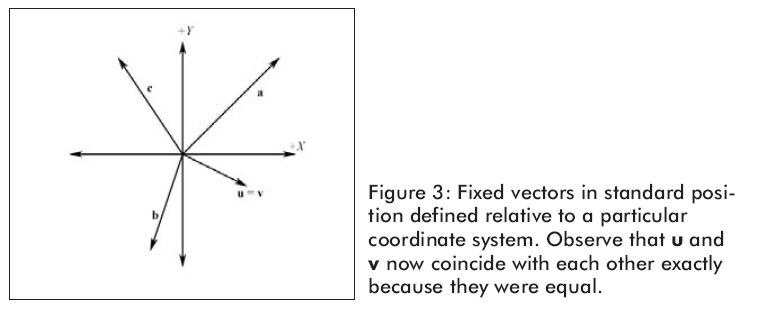
因為向量的位置不能改變它的性質,我們可以把所有向量平移使他們的尾部和坐標系的原點重合。因此,當一個向量在標準位置我們能通過頭點來描述向量。圖3顯示的是圖1中的向量在標準位置的樣子。
我們通常用小寫字母表示一個向量,但有時也用大寫字母。如2、3和4維向量分別是:
u
= (ux,
uy),
N
= (Nx,
Ny,
Nz),
c
= (cx,
cy,
cz,
cw)。
我們現在介紹4個特殊的3D向量,就象圖4顯示的。首先是都由含有0的零向量;它被表示成加粗的0
= (0, 0,
0)。接下來3個特殊的向量標準基向量。它們被叫做i,
j和k向量,分別沿著坐標系的x軸,y軸和z軸,并且有1的單位長:i
=
(1, 0, 0),
j
= (0, 1, 0), and
k
= (0, 0, 1)。
注意:只有1個單位長度的向量叫做單位向量(模長為1的向量)。

在D3DX庫中,我們能用D3DXVECTOR3類表示3維空間中的向量。它的定義是:
Note that D3DXVECTOR3
inherits its component data from D3DVECTOR,
which is defined as: