光的衰減
光隨距離衰減,所以遠離光源的物體會變暗一些。現實世界里,光強度反比于物體和光源距離的平方。
i1 / i2 = d22 / d12
公式15.12
實際光線衰減反比于距離的平方
此處i為光強,d為距離。
實踐中,公式15.12并不方便。我們常用另一個簡單的基于輻射衰減距離的模型替代,在輻射衰減距離之外,光線將完全衰減為0。通常,可在光線有效射程內使用線性插值表現光隨距離d的衰減:
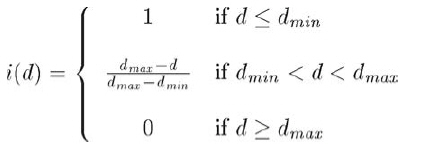
如上,實際有兩個輻射衰減距離。在dmin內,光強不衰減;dmin至dmax,光強有1減至0;超出dmax,光強一律為0。dmin控制開始衰減的距離,常設為0,表示光一旦射出即開始衰減;dmax是真正的衰減距離,此距離之外,光完全失效。
距離衰減也適用于點光源和聚光燈(平行光無衰減),聚光燈還多出一個Hotspot輻射衰減半徑,表示光亮在光錐邊上的衰減。一旦計算出衰減系數i,即可將它乘以鏡面反射分量和漫反射分量。記住環境光是不衰減的,這很顯然。
光照方程----合成
前面分別討論了光照方程的各分量,現在是把它們合成到一起的時候了:
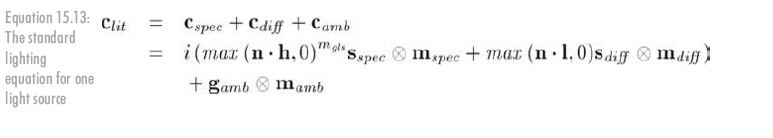
圖15.16顯示了當光分量獨立存在時,各分量的視覺效果:
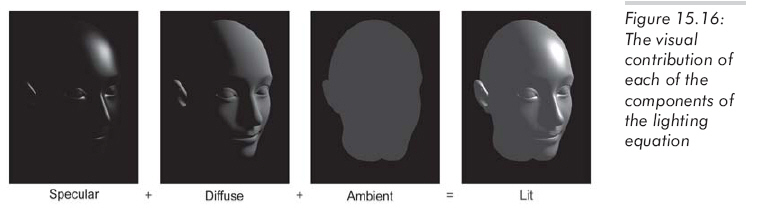
有幾點需要注意:耳朵和鼻子一樣亮,其實它本應該在頭部的影子中。這是采用局部光照的結果,要計算陰影,必須考慮其他高級技術,影子涉及全局光照。前兩幅圖中,因為沒有環境光,頭背向光源的部分為全黑。若想照亮物體的背向部分,必須使用環境光,或者在場景中設置更多的光源,使得所有面都能被直接照亮。當只有環境光時,只能看出輪廓。光照是使物體呈現3D外觀的重要武器,為了避免這種卡通效果,我們可以使用足夠多的光源使場景中的所有表面都被直接照亮。
當有多個光源時,光照方程如何工作?對所有光源求和即可。若Sj表示第j個光源,j從1...n,n是光源個數,光照公式如下:
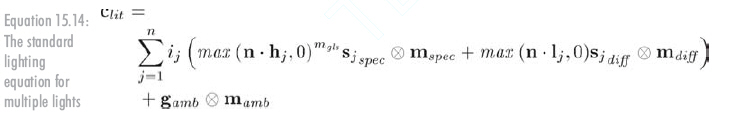
當然因為環境光只有一個,所以不做求和。
霧化
現實中,光線被空氣中無數粒子反射與折射。如果單位體積內粒子的濃度足夠,則它們是可見的,例如煙、灰塵、霧等。計算機圖形學中,上述現象都是通過霧化技術加以模擬的。想象我們正在注視遠處的物體,眼睛與物體間的光線受到大量粒子的擾動。一些原來直線傳播無法進入眼睛的光線,被那些粒子反射而進入眼睛,這就是我們"看到"空氣中粒子的原因。最后的視覺效果上,物體的顏色向霧的顏色偏移,粒子越多,偏移越大。
霧濃度在[0, 1]間取值,控制霧化程度。濃度0表示無霧化,濃度1表示完全霧化,這時像素呈現霧的顏色,最終的顏色值由物體顏色和霧顏色線性插值求得。如何計算霧濃度?前面提到,大氣中粒子越多,霧化越顯著。然而,如何知道粒子數并轉化為霧濃度呢?幸運的是,不必確切知道粒子數,我們用另一個值模擬這個數。粒子數依賴兩個因素:場景中的全局武濃度和眼睛與物體間的距離。
眼睛與物體間的距離容易得到。于是,剩下的就是根據這個距離由霧濃度求得像素顏色。如何定義霧的濃度和單位呢?我們不直接定義,而是用一個簡化系統。霧濃度由兩個距離dmin和dmax控制,像素和眼睛距離小于dmin時無霧化,隨著距離的增大,霧化逐漸加重,當距離大于dmax時完全霧化。如公式15.15所示:
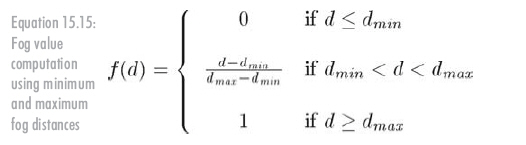
有兩點注意事項:
(1)該公式假設霧是空間均勻的,但實際情況并不總是如此。例如,現實世界中,霧常在下方較濃,此模型不能表達這個現象。
(2)距離的定義是可變的。當然,可以用歐式距離,得到球狀霧效果,但需要做開方運算。有一種簡化是以攝像機空間深度z為距離,從而得到線性霧。它的優點是速度快,但有一個惱人的副作用,某一點霧濃度可能因攝像機朝向的不同而改變,現實世界中這是不可能的。
一旦得到[0, 1]間的霧濃度,像素顏色就可以用如下線性插值公式計算:
cfogged = clit + f(gfog
- clit)
其中:
(1)clit為計算光照后的物體表面顏色
(2)f為公式15.15得出的霧濃度
(3)gfog為全局霧顏色
(4)cfogged為最終效果
為了在場景中得到霧化效果,必須向API說明霧的性質。常需要下列三種信息:
(1)霧化開關,如果要得到霧化效果,必須打開。
(2)霧的顏色,即上式的gfog。
(3)霧化距離,dmin和dmax。