逐片操作
三角網格是頂點和三角形的列表。三角網格的一系列基本操作都是逐點和逐三角形應用基本操作的結果。最明顯的,渲染和轉換都屬于這種操作。為渲染三角網格,我們逐個三角形渲染,如要向三角網格應用轉換,如旋轉和縮放等,應逐頂點進行。
焊接頂點
當兩個或更多頂點(也許有誤差)時,將它們焊接在一起是有益處的。更加準確地說,刪除其余的,只剩一個。例如,我們要焊接圖14.9中的A和B,有兩個步驟:
(1)步驟1,掃描三角形列表,將對B的引用全部替換成對A的引用。
(2)步驟2,現在B是孤立點,將它從頂點列表中刪除。

焊接頂點的目的有兩個。首先,去除重復頂點,節約內存。這是一種重要的優化方法,使得對網格的操作(如渲染和轉換)更快。其次,使幾何上相鄰的邊在邏輯上也是相鄰的。
上面討論的是兩個頂點的焊接,實踐中,我們常常希望找出與焊接點鄰近的所有頂點。這個想法是非常直接的,但有幾個細節需要明確。
(1)焊接前應去除孤立點,我們不想讓任何未被使用的點影響正被使用的點,如圖14.10所示:

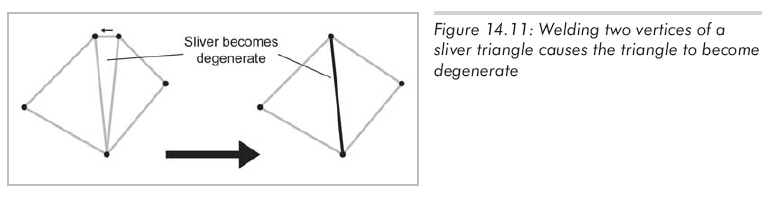
(2)當兩個頂點均來自"細長"三角形,焊接可能產生退化三角形,如圖14.11所示(這和邊縮坍類似)。這樣的三角形應被刪除,通常它們的數量并不大。焊接常會顯著減少頂點數,同時也會除去一小部分細長面。
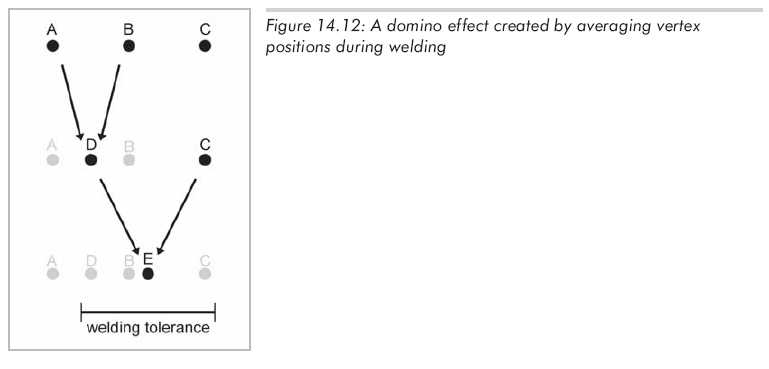
(3)焊接時,似乎應該用原頂點的平均作為新頂點,而不是簡單地選擇其中一個而拋棄另一個。這種方式不偏向任何一個頂點,,在只有少量頂點需要焊接時這似乎是個好主意。然而,焊接自動進行的時候可能引起"多米諾"效應,導致原來不在誤差容限內的多個點被焊接。
圖14.12中,點A和B在誤差容限內應被焊接。我們"聰明地"焊接這兩個點,計算A和B的平均值得到一個新的點D。現在C和D又在容限范圍內被焊接,最終產生E。結果是點A和C被焊接了,它們本不在誤差容限內的。并且,我們"聰明的"嘗試也失敗了,因為A、B和C被焊接,但結果并不是這三個點的平均。
這還不是最壞的情形,至少沒有點跑出誤差容限外去。但確實可以故意用更多頂點和不同順序制造這種惡毒的例子,更不幸的是實踐中確實存在這種問題,建模程序和自動生成程序常這么干。其實,即使不平均生成新坐標,依然會有上面的問題。例如不考慮平均坐標,以為應用一個簡單的規則"總是將高序數頂點焊接到低序數頂點"就可以解決這個問題。
有一些防止出現上述問題的方法。比如,可以先找出所有誤差容限內的頂點組,再焊接它們;或者不考慮已經焊接過的頂點;或者記錄原頂點坐標,當頂點和它們相比在容限外時就不焊接。這些方法都過于復雜,我們不應為不顯著的性能而增加復雜性。焊接是為了去除重復頂點,而不是為了網格消減:即大量減少三角形數,而盡量保持三角網外形不變。關于網格消減,必須使用更加高級的算法。
另外一個問題是關于三角網的附加信息的,如表面法向量、紋理映射坐標等。當點焊接時,先前的不連續消失了,圖14.8就是一個例子。
最后,頂點焊接的直接實現非常慢。即使在當今的硬件條件下,數千個點和面的焊接也要用掉數秒鐘。尋找焊接頂點對的算法是O(n2)復雜度的。一次焊接后的頂點索引替換需要遍歷整個三角形列表;刪除一個頂點也需要遍歷三角形列表以修復比刪除點序號高的頂點的索引。幸運的是,加以思考,我們可以找到一個快得多的算法。
面拆分
面拆分即復制頂點,使邊不再被共用,它和焊接剛好相反。顯然,面拆分會導致拓撲間斷,因為面不再鄰接。而這正是我們的目的,使得幾何間斷的地方拓撲也是間斷的(如角和邊)。圖14.13顯示了兩個三角形的拆分,盡管我們把兩個三角形分開以顯示這里有多個邊和頂點,這只是為了顯示,頂點沒有移動,新的頂點和邊其實是重合的。
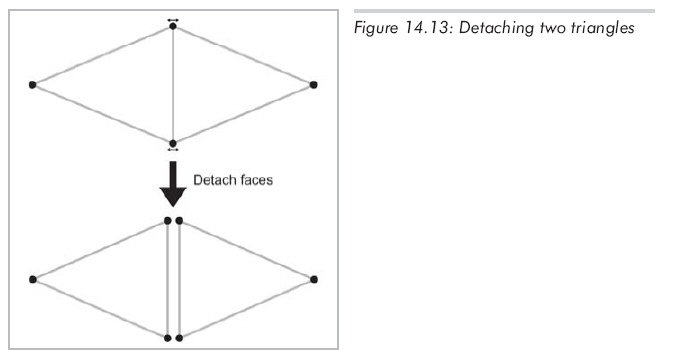
實踐中,我們經常要拆分所有面。
邊縮坍
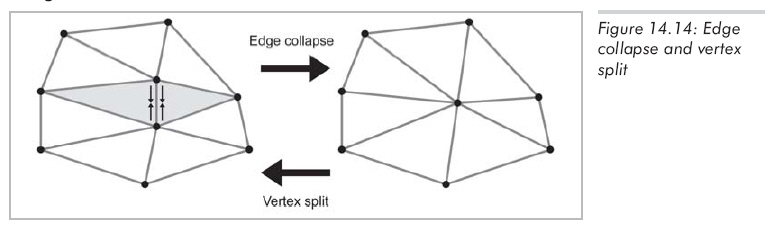
邊縮坍是將邊縮減為頂點的方法,與之對應的是頂點拆分。如圖14.14所示,注意到邊縮坍使邊的兩個頂點變為一個,共享該邊的三角形(圖14.14中陰影部分)消失。邊縮坍常用于網格消減,因為它減少了頂點和三角形數量。
網格消減
網格消減是將三角形和頂點數較多的網格變為三角形和頂點數相對較少的網格,并且要求網格外觀和主要頂點盡可能保持不變。Hugues
Hoppe指出zhi只用邊縮坍就可以達到好的效果,選擇要縮坍的邊相對費時,視啟發方法的復雜性而定。盡管選取縮坍對象的時間較長,但縮坍操作本身并不復雜。我們可將此過程離線記錄下來,在實時需要時"重放"它,即可得到任意精細程序的風格。Hoppe的論文描述了如何利用頂點拆分來反演邊縮坍過程,用此反演法生成的網格稱為漸進式網格。