三角帶
三角帶是一個(gè)三角形列表，其中每個(gè)三角形都與前一個(gè)三角形共享一邊，圖14.2顯示了一個(gè)三角帶的例子。
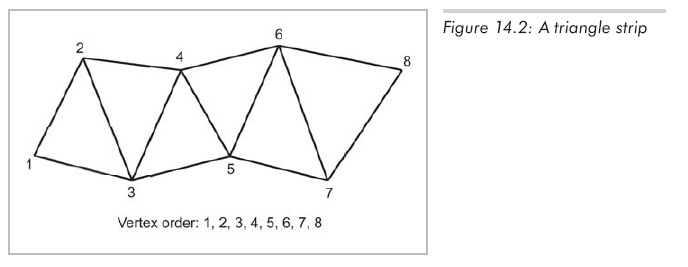
注意頂點(diǎn)列出的順序使得每三個(gè)連續(xù)的點(diǎn)都能構(gòu)成一個(gè)三角形。例如：
（1）頂點(diǎn)1、2、3構(gòu)成第一個(gè)三角形。
（2）頂點(diǎn)2、3、4構(gòu)成第二個(gè)三角形。
（3）頂點(diǎn)3、4、5構(gòu)成第三個(gè)三角形。
在圖14.2中，頂點(diǎn)以構(gòu)成三角形帶的順序編號(hào)。"索引"信息不再需要，因?yàn)轫旤c(diǎn)順序已經(jīng)隱式定義了三角形。通常，列表前部有頂點(diǎn)數(shù)目，或末尾處有一特殊碼表示"列表結(jié)束"。
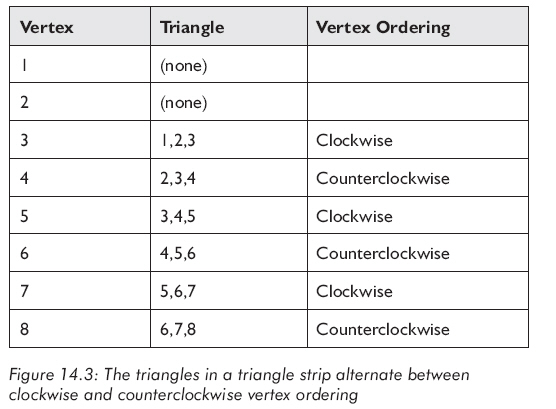
注意到，頂點(diǎn)順序在順指針和逆時(shí)針間不斷變換（見圖14.3）。某些平臺(tái)上，需要指出第一個(gè)三角形的頂點(diǎn)順序，而有些平臺(tái)上順序是固定的。
最佳情況下，三角帶可用n+2個(gè)頂點(diǎn)存儲(chǔ)n個(gè)面。n很大時(shí)，每個(gè)三角形平均發(fā)送一個(gè)頂點(diǎn)，遺憾的是，這只是最佳情況。實(shí)踐中，很多網(wǎng)格是一個(gè)三角形帶無法表達(dá)的，不僅如此，3個(gè)以上三角形共享的頂點(diǎn)還是要多次發(fā)送給圖形卡。從另一方面說，每個(gè)三角形至少要發(fā)送一個(gè)頂點(diǎn)。但在頂點(diǎn)緩存機(jī)制中，有可能將每個(gè)三角形發(fā)送的頂點(diǎn)數(shù)降到一個(gè)以下。當(dāng)然，頂點(diǎn)緩存需要額外的簿記信息（索引和緩存管理數(shù)據(jù)），可是盡管這些額外信息對(duì)單個(gè)頂點(diǎn)來講相對(duì)較大，操作速度也會(huì)相對(duì)下降，但發(fā)送頂點(diǎn)數(shù)最少的系統(tǒng)在特定平臺(tái)上速度最快。
假設(shè)用一種生成三角帶的直接方法，用三角帶表示三角網(wǎng)需要的頂點(diǎn)數(shù)為t+2s，t為三角形數(shù)目，s為三角帶數(shù)目。每個(gè)三角帶的第一個(gè)三角形對(duì)應(yīng)三個(gè)頂點(diǎn)，以后每個(gè)三角形對(duì)應(yīng)一頂點(diǎn)。因?yàn)槲覀兿Ｍ钚』l(fā)往圖形卡的頂點(diǎn)數(shù)，所以三角帶的數(shù)目應(yīng)盡可能少，即三角帶越長越好。STRIPE方法給出了一種三角帶數(shù)目接近理論下限的生成手段。
另一個(gè)希望減少三角形帶數(shù)目的原因在于建立各三角形需要額外時(shí)間。從另一方面說，分別渲染兩個(gè)長為n的三角帶所需時(shí)間長于渲染一個(gè)長為2n的三角帶，即使這個(gè)三角帶中的三角形數(shù)多于兩個(gè)分開帶中三角形數(shù)量的和。于是，我們經(jīng)常通過使用退化三角形連接多個(gè)三角帶，從而將整個(gè)網(wǎng)格置于一個(gè)連續(xù)的三角帶中，退化的意思是面積為0。圖14.4顯示了如何重復(fù)頂點(diǎn)以將兩個(gè)三角形合并為一個(gè)。
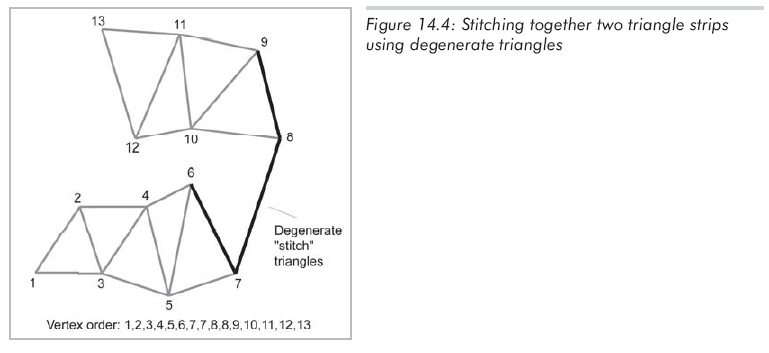
圖14.4的含義不太明顯，但這里有四個(gè)退化三角形用于連接兩個(gè)三角帶從而維持正確的順指針、逆時(shí)針順序。頂點(diǎn)7、8間的邊實(shí)際包含兩個(gè)退化三角形，圖14.5指出了圖14.4中包含的三角形。
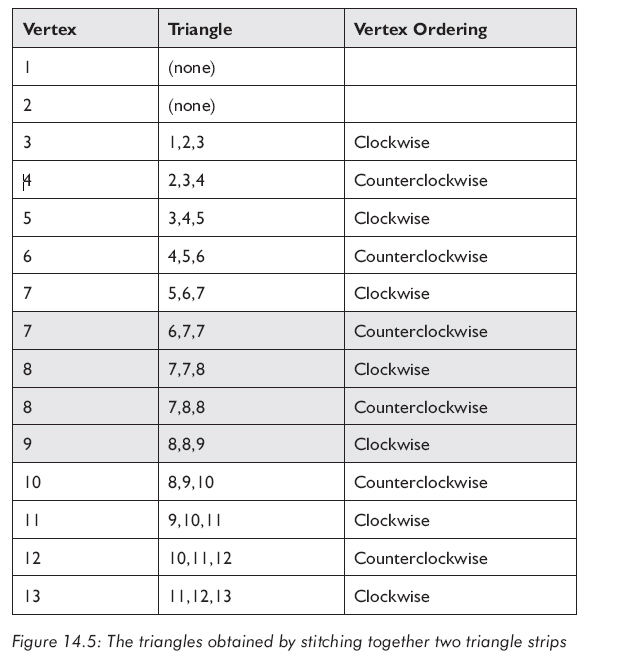
退化三角形面積為0不需要渲染，所以不會(huì)影響效率。實(shí)際上要發(fā)送到圖形卡的頂點(diǎn)仍然只是第一列的頂點(diǎn)：
1，2，3，4，5，6，7，8，9，10，11，12，13
這符合我們每三個(gè)連續(xù)頂點(diǎn)表示一個(gè)三角形的約定。
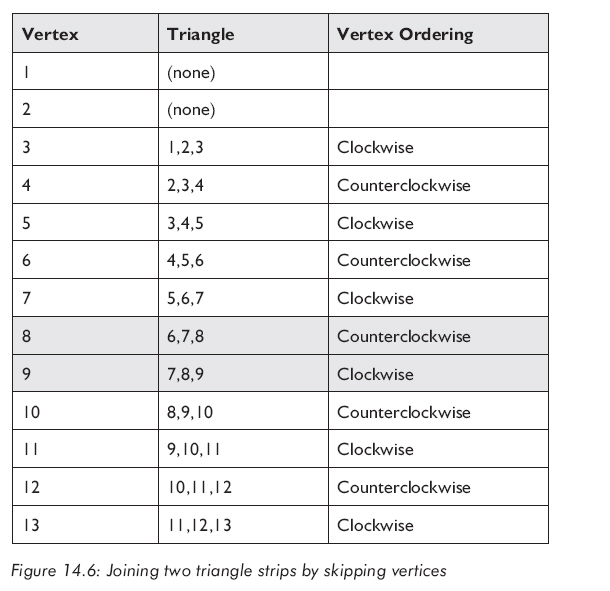
一些硬件（如PS2上的GS）可以跳過三角帶中的三角形，方法是通過一個(gè)頂點(diǎn)上的標(biāo)志位指出"不必繪制"此三角形。這給我們一種方法可以有效的從任意點(diǎn)開始新三角形帶而不必重復(fù)頂點(diǎn)或使用退化三角形。例如，圖14.4中的兩個(gè)三角帶可以如圖14.6那樣連接，其中灰色表示頂點(diǎn)被標(biāo)記"不必繪制"。
三角扇
三角扇和三角帶類似，但不如三角帶靈活，所以很少使用。圖14.7所示即為三角扇。
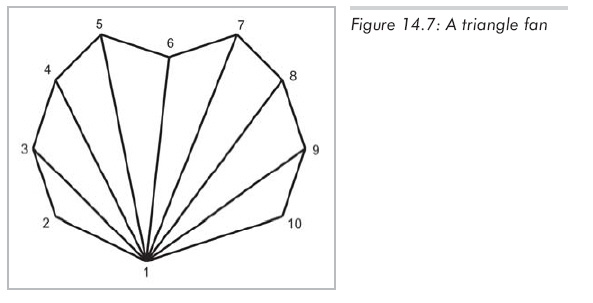
三角扇使用n+2個(gè)頂點(diǎn)存儲(chǔ)n個(gè)面，和三角帶相同。但是，第一個(gè)頂點(diǎn)必須為所有三角形共享，所以實(shí)踐中不太經(jīng)常能找到大型三角扇應(yīng)用的場(chǎng)合。并且，三角扇不能像三角帶那樣連接。所以，三角扇只能在特殊場(chǎng)合應(yīng)用，對(duì)一般應(yīng)用來說，三角帶更靈活。