三角形
三角形在建模和圖形學中有著極其重要的位置�。復雜3D物體的表面,如車或人體,都是用三角形模擬的�,像這樣一組相連的三角形稱作三角網格�。
基本性質
三角形是通過列出它的三個頂點來定義的�����。這些點的順序是非常重要的,在左手坐標系中���,當從三角形"正面"看時,經常以順時針方向列出這些點�����,設這三個頂點為v1�����、v2�����、v3�����。三角形位于一個平面中���,這個平面的方程(法向量n和到原點的距離d)在很多應用中非常重要���。
讓我們標出圖12.16中的三角形內角�、順時針邊向量�、邊長。
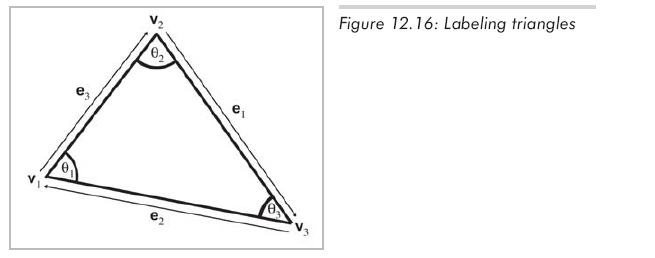
設Li為ei的長度,注意ei、Li和vi的對應關系���,vi為相應下標的頂點,它們的關系如下:
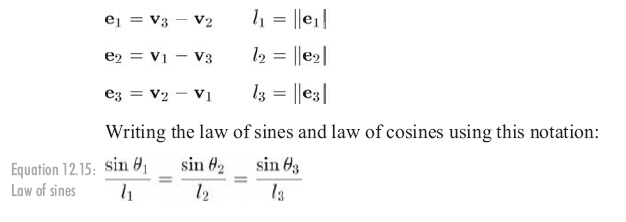
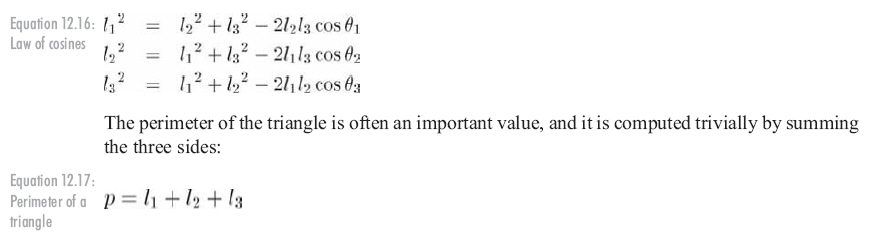
面積
最經典的計算方法是用底和高計算面積,觀察圖12.17中的平行四邊形及其包含的三角形���。
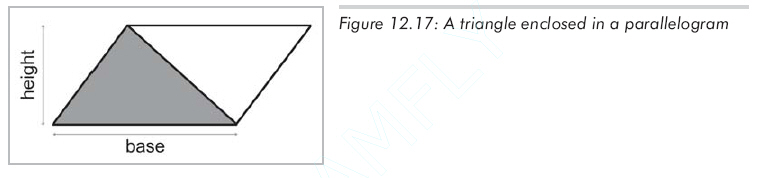
由經典幾何可知,平行四邊形面積等于底和高的乘積。因為三角形恰好占了這個面積的一半,所以由底和高給出的三角形面積公式為(公式12.18):
A = bh/2
公式12.18
三角形面積是平行四邊形面積的一半
如果不知道高,可以使用海倫公式計算面積���,它只需要提供三邊的長度即可。設s為周長的一半(也稱作半周長),如公式12.19所示:
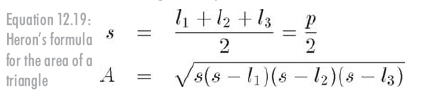
海倫公式非常有用���,因為它在3D中使用非常方便。
有時候�����,高和周長都沒有直接提供�����,所知道的只有頂點的笛卡爾坐標�����。(當然�,總是可以從坐標中算出邊長,但在某些情況下�����,我們想要避免這種代價相對較高的計算�����。)讓我們看看能否從頂點坐標直接計算面積�����。
先在2D中解決這個問題�����。基本思想是���,對三角形三邊中的每一邊,計算上由該邊���,下由x軸所圍成的梯形的有符號面積(如圖12.18
所示)。
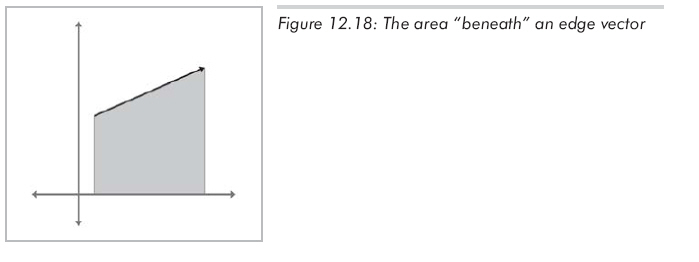
"有符號面積"是指:如果邊的端點是從左向右的�,則面積為正���;如果邊的端點是從右向左的�,則面積為負�����。注意不管三角形的方向如何變化,都存在至少一個正邊和一個負���,一個豎直邊的面積為0。各邊下面區域的面積分別為:
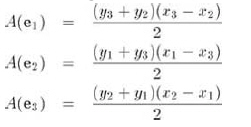
即使一部分(或整個)三角形擴展到了x軸下邊�,上面的公式依然正確�����。
這三個梯形的有符號面積相加,就得到了三角形本身的面積�。事實上���,能用同樣的思想計算任意多邊形的面積�����。
這里,假設頂點是按順指針列出的�����,如果頂點以相反的順序列出�,面積的符號將變負。將這三個梯形的面積相加�,計算三角形的有符號面積:
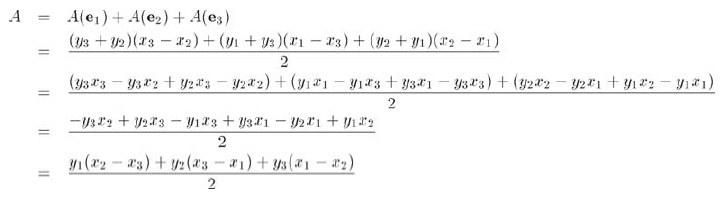
實際上���,還能進一步簡化���?;舅枷胧?,平移三角形不會改變三角形的面積。因此,我們可以在豎直方向上平移三角形�����,從每個y坐標中減去y3���,如公式12.20所示�����。(用代數變換也能得到這個簡化形式。)
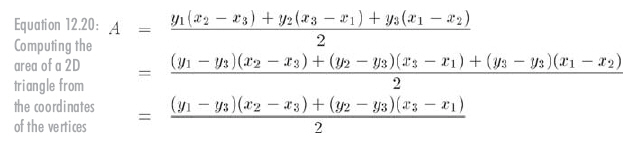
在3D中,可以通過叉乘來計算三角形的面積�。兩向量a�����、b叉乘的大小等于以a、b為兩邊的平行四邊形的面積。因為三角形面積等于包圍它的平行四邊形的一半,所以我們有了一種簡便方法。給出三角形的兩個邊向量���,e1和e2,則三角形面積為:
A = || e1 x e2 || / 2