特殊的2D直線表示方法
2D中,可以使用公式12.3隱式表示直線:
ax + by = d
公式12.3 2D直線的隱式定義
另一種表示方法為,設向量n = [a, b],用向量記法將公式12.3寫為公式12.4的形式:
p . n = d
公式12.4 用向量記法的2D直線的隱式定義
當?shù)仁絻蛇呁艘猿?shù)k時,n和d會發(fā)生變化但這并不會改變直線的定義。如果n為單位向量,大多數(shù)情況下計算會很方便。
再換一種表示方法,變換等式,將直線表示為斜截式,見公式12.5:
y = mx + b
公式12.5 斜截式
m是直線的"斜率",等于rise和run的比值:每向上移動rise單位,就會向右移動run單位。b是y截距(不同于第一種隱式法中的b)。b之所以稱為y截距,是因為直線和y軸相交于此。將x=0代入上述等式,就可以清楚地看出直線和y軸交于y=b。如圖12.5所示:
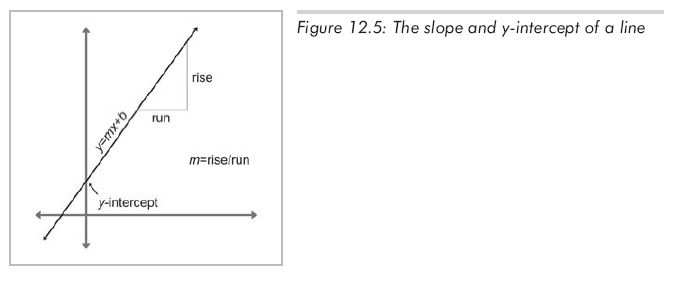
水平直線的斜率為0,豎直直線的斜率為無窮大,不能用斜截式表示。豎直直線的隱式表示為:
x = k
另一種描述直線的方法是給出垂直于直線的標準向量n和原點到直線的垂直距離d。標準向量描述了直線的方向,距離則描述了直線的位置。如圖12.6所示:

注意,這只是公式12.4的一種特殊情況。n是垂直于直線的單位向量,d給出了原點到直線的有符號距離。這個距離是在垂直于直線的方向(平行于n)上度量的。有符號距離的意思是如果直線和標準向量n代表的點在原點的同一側(cè),則d為正。當d增大時,直線沿方向n移動。
一種變形是用直線上的點來描述直線的位置而不是用原點到直線的距離。當然,直線上的任意點都可以。直線的方向仍然用垂直于直線的標準向量n表示,如圖12.7所示:
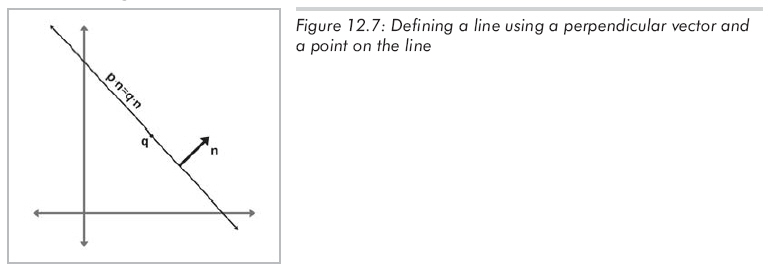
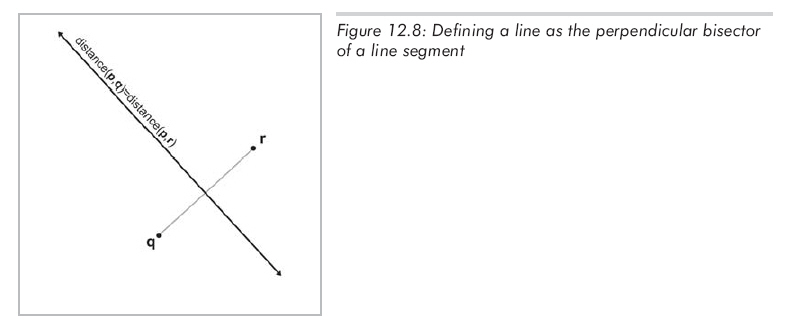
最后一種定義是將直線作為兩個點q和r的垂直平分線,如圖12.8所示。事實上,這也是直線最早的一種定義:到兩個給定點距離相等的點的集合。
在不同表示方法間轉(zhuǎn)換
注意,直線的表示方法僅適用于2D。
從射線的兩點定義式轉(zhuǎn)換到參數(shù)形式:
p0 = porg
d = pend - porg
相反的轉(zhuǎn)換,從參數(shù)形式轉(zhuǎn)換到兩點定義的形式:
porg = p0
pend = p0 + d
如果給定一條射線的參數(shù)形式,就能夠從中計算出包含該射線的直線的隱式表示:
a = dy
b = -dx
d = porgdy - porgdx
直線的隱式轉(zhuǎn)換到斜截式:
m = -a/b,b = d/b
注意,等號左邊的b是斜截式 ---- y = mx + b中的b;等號右邊的b則是隱式ax
+ by = d中y的系數(shù)。
從直線的隱格式轉(zhuǎn)換到"標準向量 + 距離"形式:
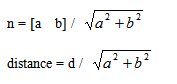
從"標準向量 + 直線上的點"形式轉(zhuǎn)換到"標準向量
+ 距離"形式(設n為標準向量):
n = n
distance = n . q
最后,從垂直平分線形式轉(zhuǎn)換到隱格式:
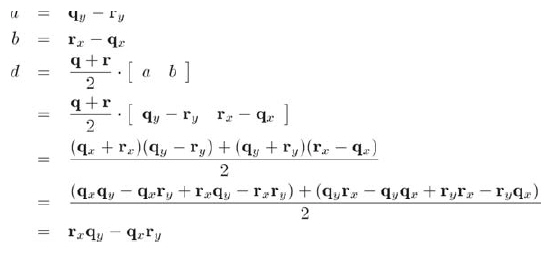
球和圓
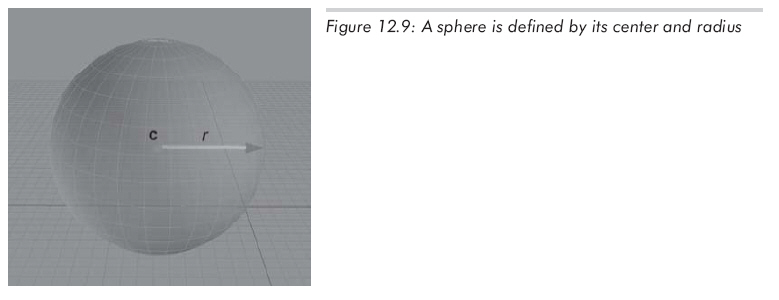
球是一種3D物體,定義為到給定點的距離為給定長度的所有點的集合。球面上某點到球心的距離稱作球的半徑,球的直接表示形式能描述出球心c和半徑r,如圖12.9所示:
球的簡單性使它在計算幾何和圖形學中幾乎無處不在。"邊界球"經(jīng)常用于相交性測試中,因為檢驗與一個球是否相交是非常簡單的。而且由于旋轉(zhuǎn)一個球時并不會改變它的形狀,所以使用邊界球時不必考慮物體的方向。
由球的定義可以直接導出它的隱式表示形式:到球心的距離為給定距離的點的集合。球心為c,半徑為r的球的隱式表示形式為:
|| p - c || = r
公式12.6 向量記法的球的隱式表示
注意p是球表面上的任意一點。如果要讓球內(nèi)部的點p也滿足這個式子,就必須將等號換為"≤"。公式12.6也是2D圓的隱式表示,將公式12.6在3D中展開,兩邊同時平方得到公式12.7:
(x - cx)2 + (y - cy)2
+ (z - cz)2 = r2
公式12.7 球的隱式定義
我們能計算圓和球的直徑(經(jīng)過圓心的直線與圓有兩個交點,這兩個交點間的距離稱作直徑)和周長(繞圓一周的長度即為周長),見公式12.8:
D = 2r
C = 2πr = πD
公式12.8 圓的直徑和周長
公式12.9為圓的面積:
A = πr2
公式12.9 圓面積
球的表面積S及體積V的計算方式如公式12.10所示:
S = 4πr2
V = 4/3 πr3
公式12.10 球的表面積和體積
如果學過微積分,你會發(fā)現(xiàn)一個非常有趣的現(xiàn)象:圓面積的微分是圓周長,球體積的微分是球表面積。