隱式表示
通過定義一個布爾函數f(x, y , z),我們能夠隱式表示一個圖元。如果所指定的點在這個圖元上,這個布爾函數就為真;對于其他的點,這個布爾函數為假。例如等式:
x2+y2+z2 = 1
對中心在原點的單位球表面上的所有點為真,隱式表示法用于測試圖元是否包含某點時非常有用。
參數形式表示
圖元也能以參數形式表示。我們從一個簡單的2D例子開始,定義如下兩個關于t的函數:
x(t) = cos2πt
y(t) = sin2πt
這里t被稱作參數,并和所用的坐標系無關。當t從0變化到1時,點(x(t),y(t))的軌跡就是所要描述的形狀。這組等式表示的是一個中心在原點的單位元(如圖12.1所示):
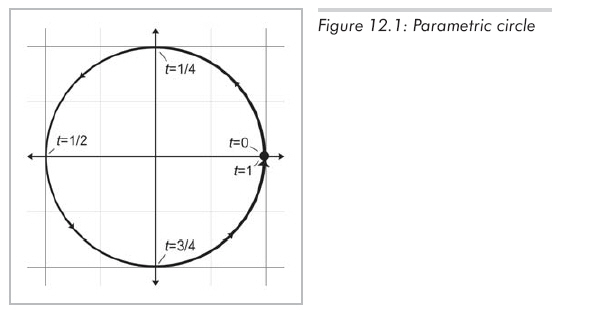
盡管可以讓t在我們想要的任意范圍內變化,但是在大多數情況下,把參數的變換范圍限制在0到1之間會比較方便一些。另一種常見的變換范圍是從0到L,L是圖元的"長度"。
如果函數只使用一個參數,就稱這些函數為單變量的,單變量函數的軌跡是一條曲線。有時候函數可能有多于一個的參數,雙變量函數接受兩個參數,經常設為s和t,雙變量函數的軌跡是一個曲面。
直接形式表示
我們將這組表示方法命名為直接法,是因為沒有更好的術語來描述它們。它們隨圖元的類型而變化,而且經常能直接體現圖元最本質和明顯的信息。例如,用兩個端點來表示一個線段,用球心和半徑來表示一個球。直接形式是最便于人們直接使用的形式。
自由度
每個幾何圖元都有一個固有的屬性:自由度。自由度是無歧義地描述該實體所需信息量的最小數目。有趣的是,同一幾何圖元,不同表示方法所用到的自由度是不同的。然而,我們會發現"多余"的自由度數量經常是由于圖元參數化中的冗余造成的,這些冗余可以通過一些適當的假設條件來消除,如假設向量為單位長度。
直線和射線
在經典幾何中,仍使用的是下列定義:
(1)直線向兩個方向無限延伸。
(2)線段是直線的有限部分,有兩個端點。
(3)射線是直線的"一半",有一個起點并向一個方向無限延伸。
在計算機科學和計算幾何中,存在著這些定義的許多變種。這里仍使用直線和線段的經典定義,但對射線的定義做出修改:
(4)射線就是有向線段。
對我們來說,射線有起點和終點。這樣,一條射線定義了一個位置,一個有限長度和一個方向(除非射線長度為0)。任何射線都定義了包含這個射線的一條直線和線段。射線在計算幾何和圖形學中占有非常重要的位置。如圖12.2:
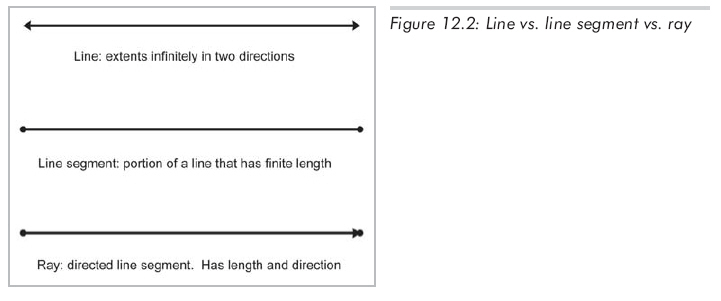
兩點表示法
描述射線最直觀的方法是給出兩個端點:起點Porg和終點Pend,如圖12.3所示:

射線的參數形式
2D和3D射線都能用參數形式表示,2D射線的參數形式使用兩個函數,如公式12.1所示:
x(t) = x0 + t△x
y(t) = y0 + t△y
公式12.1 2D射線的參數形式
3D射線是對2D的一種直接擴展,只需加上第三個函數z(t)即可,參數t的范圍從0到
1。
向量記法能使射線的參數形式更加緊湊,在任意維度中表示射線都可以用這種形式。如公式12.2所示:
p(t) = p0 + td
公式12.2 用向量記法表示的射線參數形式
射線的起點p(0) = p0 這樣,p0指定了射線的位置信息,同時增量向量d指定了它的長度和方向。射線的終點p(1)
= p0 + d,如圖12.4 所示:

在一些相交性測試中,我們可能使用公式12.2的一種變形:d為單位向量,參數t從0變化到L,L是射線的長度。