新建網頁 1
四元數樣條 ---- “squad”
Slerp提供了兩個方位間的插值,當有多于兩個的方位序列(它描述了我們想要經過的插值“路徑”)時怎么辦?我們可以在”控制點“之間使用slerp。類似于基本幾何學中的線性插值,控制點之間是以直線連接的。顯然,控制點上會有不連續性 ---- 這是我們想要避免的,我們給出squad(Spherical and Quadrangle)的公式,用來描繪控制點間的路徑。
設控制點由四元數序列所定義:
q1,q2,q3,…qn-2,qn-1,qn
另外,引進一個輔助四元數si,將它作為臨時控制點:
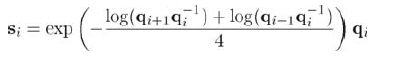
注意,qi-1至qi+1計算出si,所以s1和sn是未定義的。換句話說,曲線從q2延伸到qn-1,第一個和最后一個控制點僅用于控制中間的曲線。如果曲線一定要經過這兩點,必須在頭部和尾部增加虛控制點,一個顯而易見的方法就是復制這兩個控制點。
給定四個相鄰的控制點,squad用于計算中間兩點間的插值,這點非常像三次樣條。
設四個控制點為: qi-1,qi,qi+1,qi+2
還要引入一個插值變量h,h從0變化到1時,squad描繪qi到qi+1之間的曲線。
整條插值曲線能夠分段應用squad方法來獲得,如公式10.12所示:
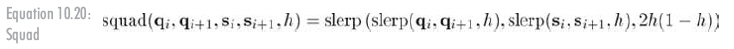
四元數的優點和缺點
四元數有一些其他角位移表示方法所沒有的優點:
(1)平滑插值。slerp和squad提供了方位間的平滑插值,沒有其他方法能提供平滑插值。
(2)快速連接和角位移求逆。四元數叉乘能將角位移序列轉換為單個角位移,用矩陣作同樣的操作明顯會慢一些。四元數共軛提供了一種有效計算反角位移的方法,通過轉置旋轉矩陣也能達到同樣的目的,但不如四元數來得容易。
(3)能和矩陣形式快速轉換。四元數和矩陣間的轉換比歐拉角與矩陣之間的轉換稍微快一點。
(4)僅用四個數。四元數僅包含4個數,而矩陣用了9個數,它比矩陣"經濟"得多(當然仍然比歐拉角多33%)。
要獲得這些優點是要付出代價的,四元數也有和矩陣相似的問題,只不過問題程度較輕:
(1)比歐拉角稍微大一些。這個額外的數似乎沒有太大關系,但在需要保存大量角位移時,如存儲動畫數據,這額外的33%也是數量可觀的。
(2)四元數可能不合法。壞的輸入數據或浮點數舍入誤差積累都可能使四元數不合法(能通過四元數標準化解決這個問題,確保四元數為單位大小)。
(3)難于使用。在所有三種形式中,四元數是最難于直接使用的。
各方法比較
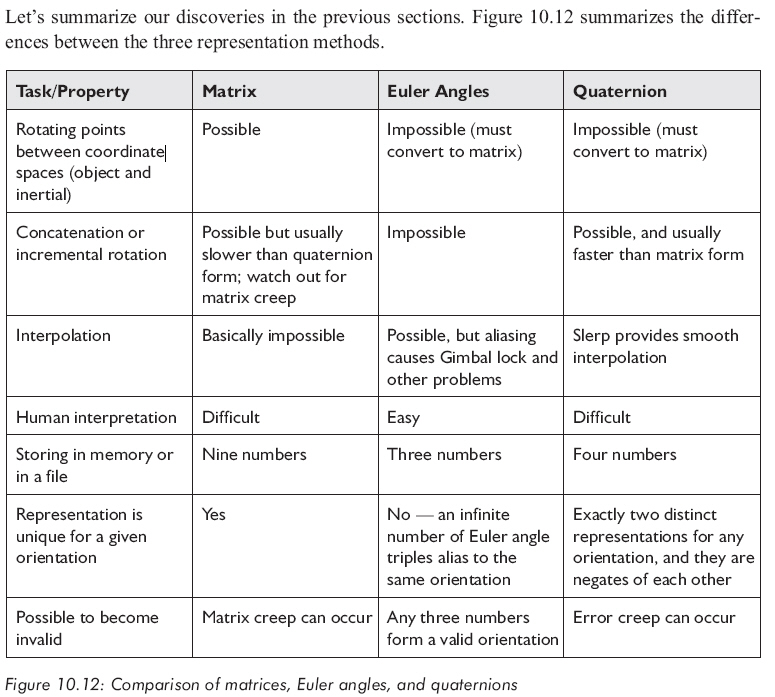
不同的方位表示方法適用于不同的情況,下面是我們對合理選擇格式的一些建議:
(1)歐拉角最容易使用。當需要為世界中的物體指定方位時,歐拉角能大大簡化人機交互,包括直接的鍵盤輸入方位、在代碼中指定方位(如為渲染設定攝像機)、在調試中測試。這個優點不應被忽視,不要以優化為名義而犧牲易用性,除非你確定這種優化的確有效果。
(2)如果需要在坐標系間轉換向量,那么就選擇矩陣形式。當然,這并不意味著你就不能用其他格式來保存方位,并在需要的時候轉換到矩陣形式。另一種方法是用歐拉角作為方位的主拷貝,但同時維護一個旋轉矩陣,當歐拉角發生改變時矩陣也要同時進行更新。
(3)當需要大量保存方位數據(如動畫)時,就使用歐拉角或四元數。歐拉角將少占用25%的內存,但它在轉換到矩陣時要稍微慢一些。如果動畫數據需要嵌套坐標系之間的連接,四元數可能是最好的選擇。
(4)平滑的插值只能用四元數完成。如果你用其他格式,也可以先轉換到四元數然后再插值,插值完畢后再轉換回原來的形式。
從歐拉角轉換到矩陣
歐拉角描述了一個旋轉序列。分別計算出每個旋轉的矩陣再將它們連接成一個矩陣,這個矩陣就代表了整個角位移。當然,它和我們是想要物體到慣性坐標的變換矩陣還是慣性到物體坐標的變換矩陣是相關的。
我們對歐拉角的定義是一個旋轉序列,該旋轉序列將物體(和它的坐標空間)從慣性坐標空間轉換到物體坐標空間。因此,可以用歐拉角定義的直接轉換來直接產生慣性 ---- 物體旋轉矩陣的一般形式:
M慣性 --> 物體 = HPB
H、P、B分別為heading、pitch、bank的旋轉矩陣,它們分別繞y、x、z軸旋轉,僅僅旋轉"坐標空間"就是旋轉"點"的嚴格相反操作。可以想象這些旋轉發生時點是固定在空間中不變的,例如,pitch使坐標空間向下,點實際上關于坐標空間向上。歐拉角公式明確指明是物體和它的坐標空間旋轉,但我們需要的是變換"點"的矩陣,所以計算矩陣H、P、B時,用相反的旋轉量來旋轉。設heading、pitch、bank的旋轉角分別為變量h、p、b:
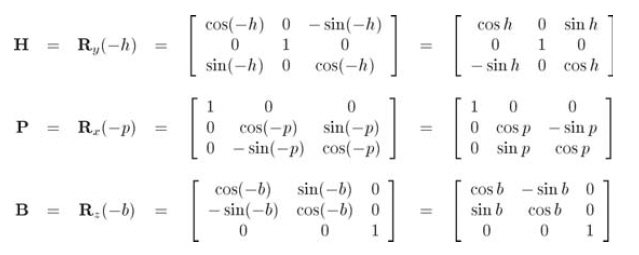
以適當的順序連接這些矩陣得到公式10.21:
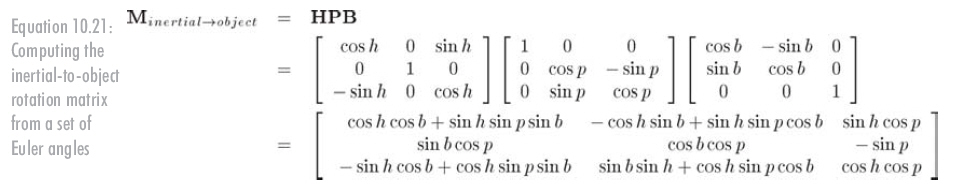
如果要從物體坐標空間變換到慣性坐標空間,應該使用慣性----物體旋轉矩陣的逆。因為旋轉矩陣是正交的,所以求它的逆就是求它的轉置,下面驗證這一點。
為了從物體坐標空間變換到慣性坐標空間,順序應該為"un-bank"、"un-pitch"、"un-heading",公式表示為:
M物體->慣性 = (M慣性->物體)-1 = (HPB)-1 = B-1P-1H-1
注意,可以認為旋轉矩陣B-1、P-1、H-1為它們對應矩陣的逆,或者是使用相反旋轉角b、p、h的一般旋轉矩陣。(慣性 --- 物體矩陣中,使用負的旋轉角,因此這里的角不用變負。)
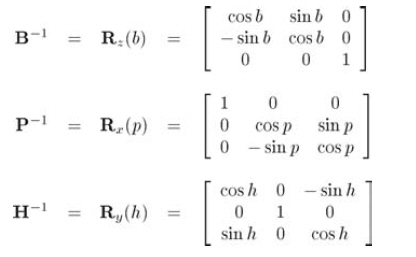
以適當的順序連接這些矩陣得到公式10.22:
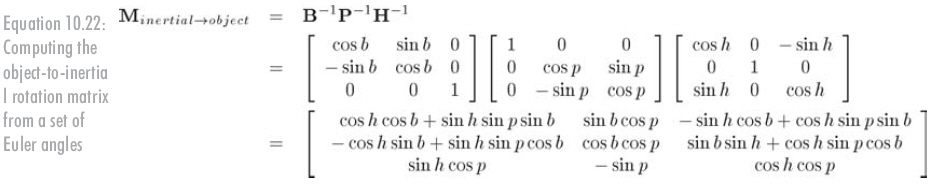
比較公式10.21和公式10.22,可以看到物體---慣性矩陣確實慣性---物體矩陣的轉置。
從矩陣轉換到歐拉角
將角位移從矩陣形式轉換到歐拉角需要考慮以下幾點:
(1)必須清楚矩陣代表什么旋轉:物體 -- 慣性還是 慣性 -- 物體,這里討論使用慣性 -- 物體矩陣的技術,物體 -- 慣性矩陣轉換成歐拉角的過程與之類似。
(2)對任意給定角位移,存在無窮多個歐拉角可以用來表示它。因為"別名"問題,這里討論的技術總是返回"限制歐拉角",heading和bank的范圍±180°,pitch的范圍為±90°。
(3)矩陣可能是病態的,我們必須忍受浮點數精度的誤差。有些矩陣還包括除旋轉外的變換,如縮放、鏡像等。這里只討論工作在旋轉矩陣上的變換。
考慮這些因素后,我們嘗試從公式10.21直接解得歐拉角:
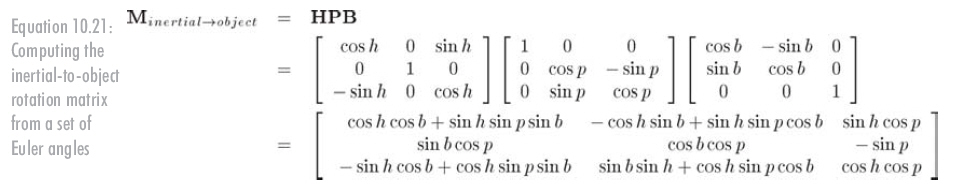

If cos p = 0, then we cannot use the above trick since all the matrix elements involved are zero.
However, notice that when cos p = 0, then p = 90°, which means we are either looking straight
up or straight down. This is the Gimbal lock situation, where heading and bank effectively rotate
about the same physical axis (the vertical axis). In this case, we will arbitrarily assign all rotation
about the vertical axis to heading and set bank equal to zero. Now we know the value of pitch and
bank, and all we have left is to solve for heading. Armed with the following simplifying
assumptions:
cosp = 0
b = 0
sinb = 0
cosb = 1
將它們代入公式10.21:
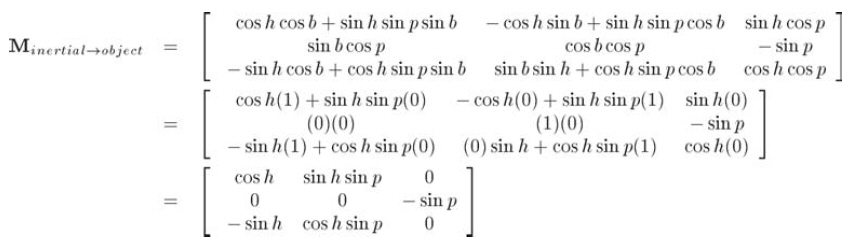
現在,能夠通過-m31和m11計算h,它們分別包含了h的sin和cos值。
讓我們看看使用上面的技術從慣性 ---- 物體旋轉矩陣中抽取歐拉角的代碼,為了使示例簡單,假設輸入輸出為全局變量。
Listing 10.3: Extracting Euler angles from an inertial-to-object rotation matrix
// Assume the matrix is stored in these variables:
float m11,m12,m13;
float m21,m22,m23;
float m31,m32,m33;
// We will compute the Euler angle values in radians and store them here:
float h,p,b;
// Extract pitch from m23, being careful for domain errors with asin(). We could have
// values slightly out of range due to floating point arithmetic.
float sp = –m23;
if (sp <= –1.0f) {
p = –1.570796f; // –pi/2
} else if (sp >= 1.0) {
p = 1.570796; // pi/2
} else {
p = asin(sp);
}
// Check for the Gimbal lock case, giving a slight tolerance
// for numerical imprecision
if (sp > 0.9999f) {
// We are looking straight up or down.
// Slam bank to zero and just set heading
b = 0.0f;
h = atan2(–m31, m11);
} else {
// Compute heading from m13 and m33
h = atan2(m13, m33);
// Compute bank from m21 and m22
b = atan2(m21, m22);
}