四元數(shù)乘法(叉乘)
四元數(shù)能根據(jù)復數(shù)乘法解釋來相乘,如下:
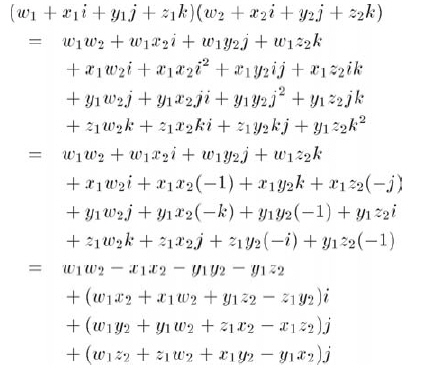
這導出了四元數(shù)乘法的標準定義,下面以兩種四元數(shù)記法給出,見公式10.9:
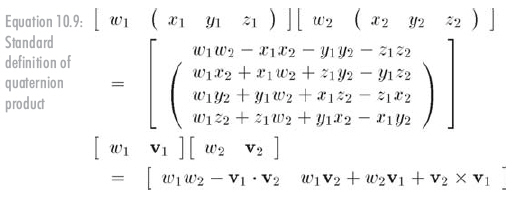
不用為四元數(shù)叉乘使用乘號,"行"或 "列"四元數(shù)也沒有什么區(qū)別。
四元數(shù)叉乘滿足結合律,但不滿足交換律,如公式10.10所示:
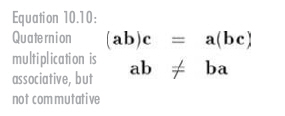
現(xiàn)在看看兩個四元數(shù)叉乘的模:
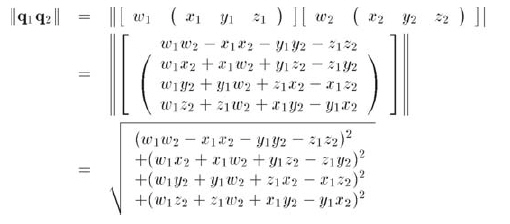
展開合并同類項:
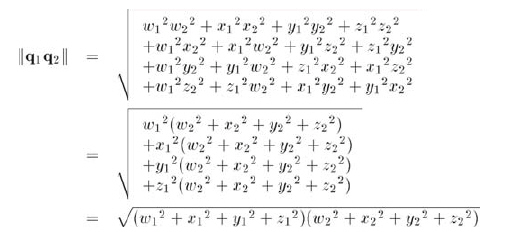
最后應用四元數(shù)模的定義得到公式 10.11:

因此,四元數(shù)乘積的模等于模的乘積。這個結論非常重要,因為它保證了兩個單位四元數(shù)相乘的結果還是單位四元數(shù)。
四元數(shù)乘積的逆等于各個四元數(shù)的逆以相反的順序相乘,如公式10.12所示:
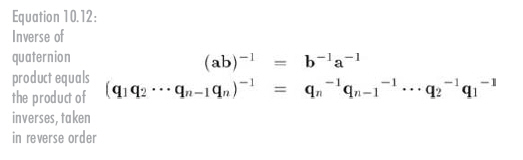
現(xiàn)在到了四元數(shù)非常有用的性質(zhì)。讓我們"擴展"一個標準3D點(x,
y, z)到四元數(shù)空間,通過定義四元數(shù)p=[0, (x, y, z)]即可(當然,在一般情況下,p不會是單位四元數(shù))。設q為我們討論的旋轉(zhuǎn)四元數(shù)形式[cos(θ/2),
nsin(θ/2)],n為旋轉(zhuǎn)軸,單位向量;θ為旋轉(zhuǎn)角。你會驚奇地發(fā)現(xiàn),執(zhí)行下面的乘法可以使3D點p繞n旋轉(zhuǎn):
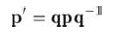
已經(jīng)證明,四元數(shù)乘法和3D向量旋轉(zhuǎn)的對應關系,更多的是理論上的意義,不是實踐上的。實際上,它幾乎和把四元數(shù)轉(zhuǎn)換到矩陣形式然后再用矩陣乘以向量所用的時間一樣。
讓我們看多次旋轉(zhuǎn)的情況,將點p用一個四元數(shù)a旋轉(zhuǎn)然后再用另一個四元數(shù)b旋轉(zhuǎn):
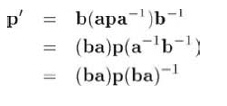
注意,先進行a旋轉(zhuǎn)再進行b旋轉(zhuǎn)等價于執(zhí)行乘積ba代表的單一旋轉(zhuǎn)。因此,四元數(shù)乘法能用來連接多次旋轉(zhuǎn),這和矩陣乘法的效果一樣。根據(jù)四元數(shù)乘法的標準定義,這個旋轉(zhuǎn)是以從右向左的順序發(fā)生的。這非常不幸,因為它迫使我們以 "由里向外"的順序連接多次旋轉(zhuǎn),這和以矩陣形式作同樣的運算是不同的(至少在使用行向量時是不同的)。
針對公式10.9所導致的"順序顛倒"問題,我們將違背標準定義,以相反的運算順序來定義四元數(shù)乘法。注意,僅僅向量叉乘部分受到了影響,見公式10.13:
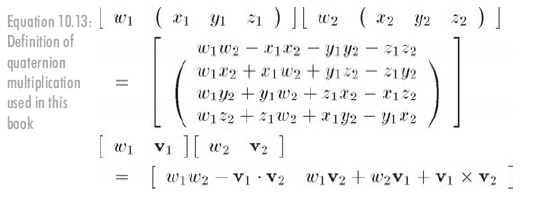
這并沒有改變四元數(shù)的基本性質(zhì)和用v、θ的幾何解釋,仍然能用四元數(shù)乘法來直接旋轉(zhuǎn)向量,唯一不同的是,根據(jù)我們的定義,將四元數(shù)放在向量右邊,而把它的逆放在向量的左邊:
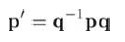
能看到下面這個表達了多個旋轉(zhuǎn)連接的等式,它是自左向右的,與旋轉(zhuǎn)發(fā)生的順序一致:
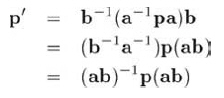
對于我們來說,讓四元數(shù)代表角位移的"高級"能力,使其易于使用,這比堅持正式標準更加重要。我們的目的在于理解四元數(shù)的本質(zhì)和它提供給我們的操作,設計一個類將直接引出這些操作,在需要的地方使用這個類,永遠不需要再去擺弄里面的數(shù)。
四元數(shù)的"差"
利用四元數(shù)的乘法和逆,就能夠計算兩個四元數(shù)的"差"。"差"被定義為一個方位到另一個方位的角位移。換句話說,給定方位a和b,能夠計算從a旋轉(zhuǎn)到b的角位移d。用四元數(shù)等式更加緊湊地表示為:ad=b。
兩邊同時左乘a-1:

現(xiàn)在,我們就有了求得代表一個方位到另一個方位角位移的四元數(shù)的方法。
數(shù)學上,兩個四元數(shù)之間的角度"差"更類似于"除",而不是真正的"差"(減法)。
四元數(shù)點乘
四元數(shù)也有點乘運算,它的記法、定義和向量點乘非常類似,如公式10.14所示:
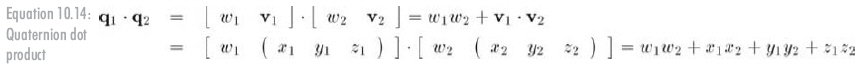
注意,和向量點乘一樣,其結果是標量。對于單位四元數(shù)a和b,有-1
≤ a . b ≤ 1。通常我們只關心
a . b 的絕對值,因為a . b = -(a
. -b),所以b和-b代表相同的角位移。
四元數(shù)點乘的幾何解釋類似于向量點乘的幾何解釋,四元數(shù)點乘 a . b
的絕對值越大,a和b代表的角位移越"相似"。