另一種描述方位的常用方法是歐拉角，這項(xiàng)技術(shù)以著名的數(shù)學(xué)家Leonhard Euler(1707 -
1783)的名字命名，他證明了角位移序列等價(jià)于單個(gè)角位移。
什么是歐拉角
歐拉角的基本思想是將角位移分解為繞三個(gè)互相垂直軸的三個(gè)旋轉(zhuǎn)組成的序列。這聽(tīng)起來(lái)很復(fù)雜，其實(shí)它是非常直觀的（事實(shí)上，易于使用正是它的主要優(yōu)點(diǎn)之一）。之所以有"角位移"的說(shuō)法正是因?yàn)闅W拉角能用來(lái)描述任意旋轉(zhuǎn)。
歐拉角將方位分解為繞三個(gè)互相垂直軸的旋轉(zhuǎn)，那么是哪三個(gè)軸？按什么順序？其實(shí)，任意三個(gè)軸和任意順序都可以，但最有意義的是使用笛卡爾坐標(biāo)系并按一定順序所組成的旋轉(zhuǎn)序列。最常用的約定是所謂的"heading
- pitch - bank"約定。在這個(gè)系統(tǒng)中，一個(gè)方位被定義為一個(gè)heading角，一個(gè)pitch角，一個(gè)bank角。它的基本思想是讓物體開(kāi)始于"標(biāo)準(zhǔn)"方位
--- 就是物體坐標(biāo)軸和慣性坐標(biāo)軸對(duì)齊。在標(biāo)準(zhǔn)方位上，讓物體作heading、pitch、bank旋轉(zhuǎn)，最后物體到達(dá)我們想要描述的方位。
如圖10.4所示，此時(shí)物體坐標(biāo)系和慣性坐標(biāo)系重合，heading為繞y軸的旋轉(zhuǎn)量，向右旋轉(zhuǎn)為正（如果從上面看，旋轉(zhuǎn)正方向就是順時(shí)針?lè)较颍?/p>
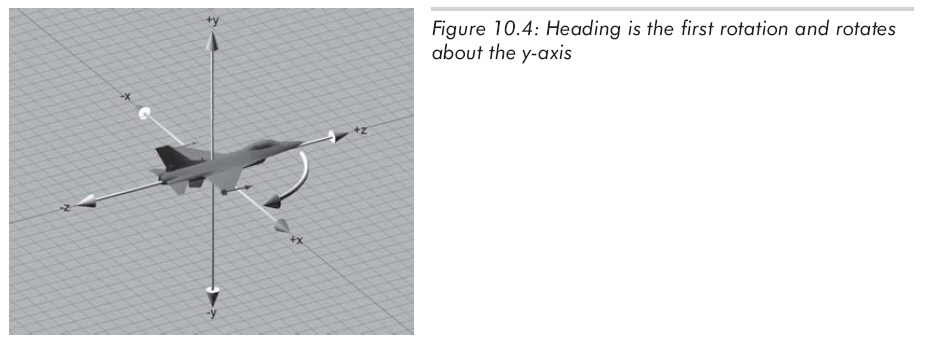
經(jīng)過(guò)heading旋轉(zhuǎn)后，pitch為繞x軸的旋轉(zhuǎn)量，注意是物體坐標(biāo)系的x軸，不是原慣性坐標(biāo)系的x軸。依然遵守左手法則，向下旋轉(zhuǎn)為正，如圖10.5所示：
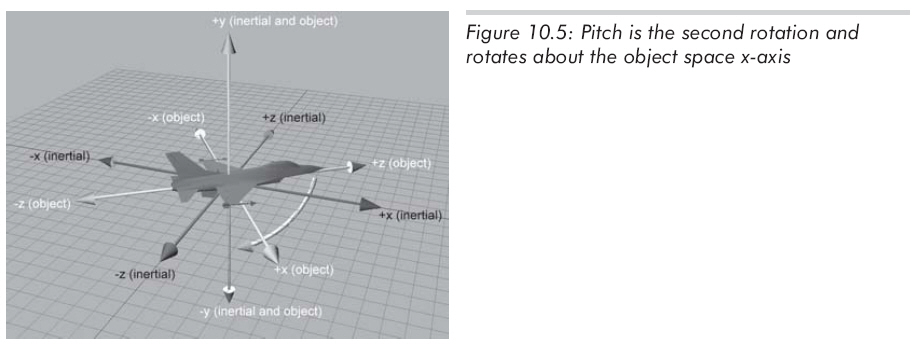
最后，經(jīng)過(guò)了heading和pitch，bank為繞z軸的旋轉(zhuǎn)量。再次提醒，是物體坐標(biāo)系的z軸，不是原慣性坐標(biāo)系的z軸。依據(jù)左手法則，從原點(diǎn)向+z看，逆時(shí)針?lè)较驗(yàn)檎?。如圖10.6所示：
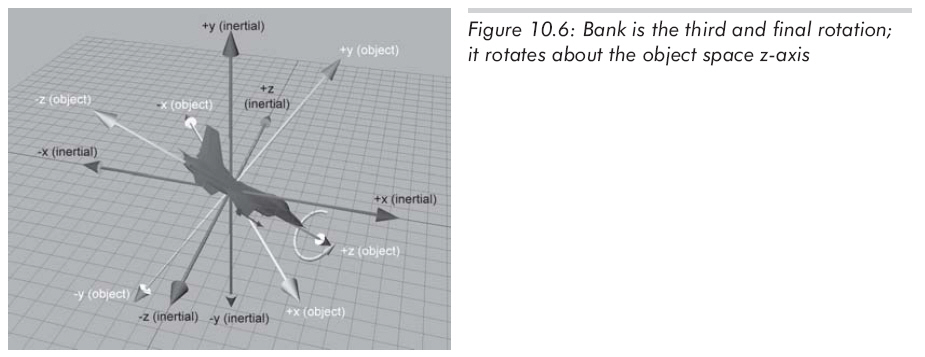
記住，當(dāng)我們說(shuō)旋轉(zhuǎn)的順序是heading-pitch-bank時(shí)，是指從慣性坐標(biāo)系到物體坐標(biāo)系。如果從物體坐標(biāo)系變換到慣性坐標(biāo)系，旋轉(zhuǎn)的順序就是相反的。"heading-pitch-bank"也叫作"roll-pitch-yaw"，roll類似于bank，yaw類似于heading（事實(shí)上，yaw并不嚴(yán)格等于heading）。注意，在roll-pitch-yaw系統(tǒng)中，角度的命名順序與從物體坐標(biāo)系到慣性坐標(biāo)系的旋轉(zhuǎn)順序一致的。
關(guān)于歐拉角的其他約定
heading-pitch-bank系統(tǒng)不是唯一的歐拉角系統(tǒng)。繞任意三個(gè)互相垂直軸的任意旋轉(zhuǎn)都能定義一個(gè)方位，所以多種選擇導(dǎo)致了歐拉角約定的多樣性：
（1）heading-pitch-bank系統(tǒng)有多個(gè)名稱。當(dāng)然，不同的名字并不代表不同的約定，這其實(shí)并不重要。一組常用的術(shù)語(yǔ)是roll-pitch-yaw，其中的roll等價(jià)于bank，yaw基本上等價(jià)于heading。注意，它的順序和heading-pitch-bank的順序相反，這只是語(yǔ)義上的。它定義了向量從物體坐標(biāo)系變換到慣性坐標(biāo)系的旋轉(zhuǎn)順序。（事實(shí)上，yaw和heading還是有技術(shù)上的差別，yaw是繞物體坐標(biāo)系y軸的旋轉(zhuǎn)，heading是繞慣性坐標(biāo)系y軸的旋轉(zhuǎn)。因?yàn)檫@里的旋轉(zhuǎn)是在物體坐標(biāo)系y軸和慣性坐標(biāo)系y軸重合時(shí)進(jìn)行的，所以這個(gè)區(qū)別并不重要。）
（2）任意三個(gè)軸都能作為旋轉(zhuǎn)軸，不一定必須是笛卡爾軸，但使用笛卡爾軸最有意義。
（3）決定每個(gè)旋轉(zhuǎn)的正方向時(shí)不一定必須遵守左手或右手法則。例如，完全可以定義pitch的正方向是向上的，并且這種定義方法非常常見(jiàn)。
（4）也是最重要的，旋轉(zhuǎn)可以以不同的順序進(jìn)行。順序并不重要，任何系統(tǒng)都能用來(lái)定義一個(gè)方位，但heading-pitch-bank順序最為實(shí)用。heading度量繞豎直軸的旋轉(zhuǎn)，它之所以有意義主要是因?yàn)槲覀兯诘沫h(huán)境經(jīng)常有某種形式的"地面"。一般來(lái)講繞慣性坐標(biāo)系的x或z軸的旋轉(zhuǎn)沒(méi)有什么意義。heading-pitch-bank順序下的另外兩個(gè)角的意義是：pitch度量水平方向的傾角，bank度量的是繞z軸的旋轉(zhuǎn)量。
歐拉角的優(yōu)點(diǎn)
歐拉角僅使用三個(gè)數(shù)來(lái)表達(dá)方位，并且這三個(gè)數(shù)都是角度。這兩個(gè)特點(diǎn)使歐拉角具有其他形式所沒(méi)有的優(yōu)點(diǎn)：
（1）歐拉角對(duì)我們來(lái)說(shuō)很容易使用。它比矩陣和四元數(shù)簡(jiǎn)單得多，這可能是因?yàn)闅W拉角中的數(shù)都是角度，符合人們思考方位的方式。如果我們選擇了與所要處理的情況最符合的約定，那么就能直接描述出最重要的角度，例如，用heading-pitch-bank系統(tǒng)就能直接地描述出偏差角度。便于使用是其最大的優(yōu)點(diǎn)，當(dāng)需要顯示方位或用鍵盤(pán)輸入方位時(shí)，歐拉角是唯一的選擇。
（2）最簡(jiǎn)潔的表達(dá)方式。歐拉角用三個(gè)數(shù)來(lái)表達(dá)方位。在3D中，表達(dá)方位不能少于三個(gè)數(shù)，如果要考慮內(nèi)存的因素，歐拉角是最合適的描述方位的方法。
（3）任意三個(gè)數(shù)都是合法的。取任意三個(gè)數(shù)，它們都能構(gòu)成合法的歐拉角，而且可以把它看成一個(gè)對(duì)方位的描述。從另一方面說(shuō)，沒(méi)有"不合法"的歐拉角。當(dāng)然數(shù)值可能不對(duì)，但至少它們是合法的。可矩陣和四元數(shù)就不一定是這樣了。
歐拉角的缺點(diǎn)
用歐拉角表達(dá)方位時(shí)的缺點(diǎn)主要有：
（1）給定方位的表達(dá)方式不唯一。
（2）兩個(gè)角度間求插值非常困難。
讓我們仔細(xì)討論這些問(wèn)題。第一個(gè)問(wèn)題是對(duì)于一個(gè)給定方位，存在多個(gè)歐拉角可以描述它。這稱作別名問(wèn)題，有時(shí)候會(huì)引起麻煩。因?yàn)檫@個(gè)原因，連一些基本的問(wèn)題（如"兩組歐拉角代表的角位移相同嗎？"）都很難回答。
第一種，在將一個(gè)角度加上360度的倍數(shù)時(shí)，我們就會(huì)遇到形式最簡(jiǎn)單的別名問(wèn)題。顯然，加上360度并不會(huì)改變方位，盡管它的數(shù)值改變了。
第二種，更加麻煩的別名問(wèn)題是由三個(gè)角度不互相獨(dú)立而導(dǎo)致的。例如，pitch135度等價(jià)于heading180度，pitch45度，然后bank180度。為了保證任意方位都只有獨(dú)一無(wú)二的表示，必須限制角度的范圍。一種常用的技術(shù)是將heading和bank限制在+180度到-180度之間，pitch限制在+90度到-90度之間。這就建立了歐拉角的一個(gè)"限制范圍"。對(duì)于任意方位，僅存在一個(gè)限制歐拉角能代表這個(gè)方位（事實(shí)上，還有一個(gè)違反唯一性的現(xiàn)象需要處理。）
歐拉角最著名的別名問(wèn)題是這樣的：先heading45度再pitch90度，這與先pitch90度再bank45度是等價(jià)的。事實(shí)上，一旦選擇+(-)90度為pitch角，就被限制在只能繞豎直軸旋轉(zhuǎn)。這種現(xiàn)象，角度為+(-)90度的第二次旋轉(zhuǎn)使得第一次和第三次旋轉(zhuǎn)的旋轉(zhuǎn)軸相同，稱作萬(wàn)向鎖。為了消除限制歐拉角的這種別名現(xiàn)象，規(guī)定萬(wàn)向鎖情況下由heading完成繞豎直軸的全部旋轉(zhuǎn)。換句話說(shuō)，在限制歐拉角中，如果pitch為+(-)90度，則bank為0。
如果是為了描述方位，特別是在使用了限制歐拉角的情況下，別名是不會(huì)造成太大的問(wèn)題的。現(xiàn)在來(lái)看兩個(gè)方位A和B間求插值的問(wèn)題，也就是說(shuō)，給定參數(shù)t，0
≤ t ≤ 1，計(jì)算臨時(shí)方位C，當(dāng)t從0變化到1時(shí)，C也平滑地從A變化到B。
這個(gè)問(wèn)題的簡(jiǎn)單解法是分別對(duì)三個(gè)角度作標(biāo)準(zhǔn)線性插值，公式如下：
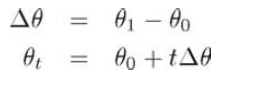
但這里面有很多問(wèn)題。
第一，如果沒(méi)有使用限制歐拉角，將得到很大的角度差。例如，方位A的heading為720度，方位B的heading為45度，720
= 360 x 2，也就是0度。所以heading值只相差45度，但簡(jiǎn)單的插值會(huì)在錯(cuò)誤的方向上繞將近兩周。如圖10.7所示：
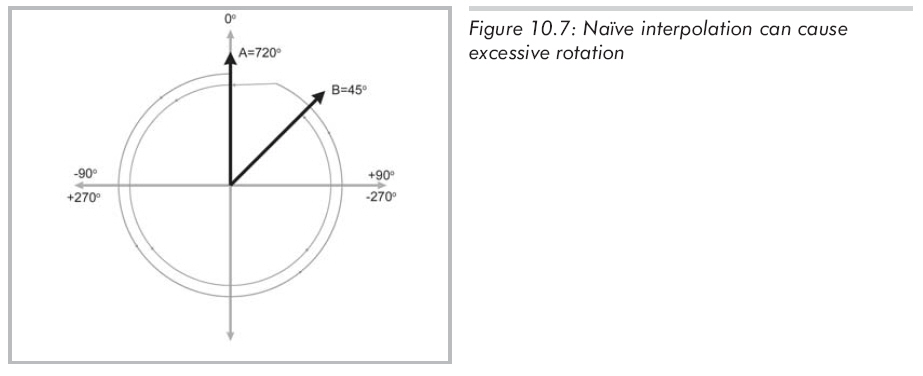
解決問(wèn)題的方法是使用限制歐拉角，然而，即使是限制歐拉角也不能完全解決問(wèn)題。插值的第二個(gè)問(wèn)題是由旋轉(zhuǎn)角度的周期性引起的。設(shè)A的heading為-170度，B的heading為170度。這些值在heading的限制范圍內(nèi)，都在-180度到180度之間。這兩個(gè)值只相差20度，但插值操作又一次發(fā)生了錯(cuò)誤，旋轉(zhuǎn)是沿 "長(zhǎng)弧"繞了340度而不是更短的20度，如圖10.8所示：
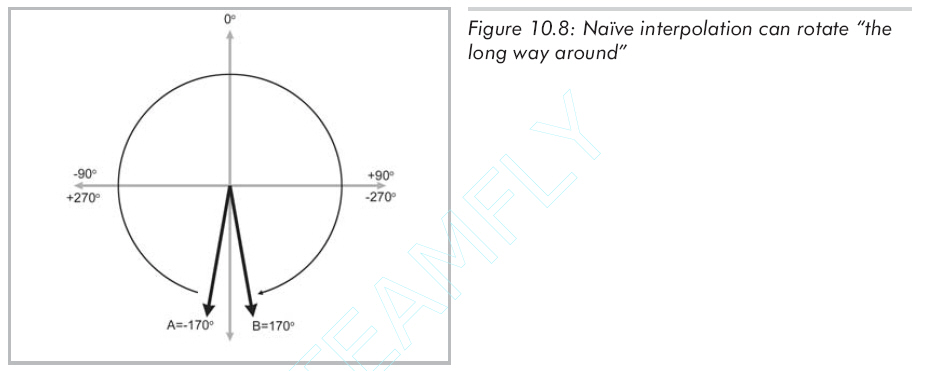
解決這類問(wèn)題的方法是將插值的"差"角度折到-180度到180度之間，以找到最短弧。
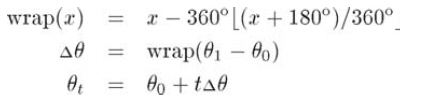
即使使用了這兩個(gè)角度限制，歐拉角插值仍然可能碰到萬(wàn)向鎖的問(wèn)題，它在大多數(shù)情況下會(huì)產(chǎn)生抖動(dòng)、路徑錯(cuò)誤等現(xiàn)象，物體會(huì)突然飄起來(lái)像是"掛"在某個(gè)地方。根本問(wèn)題是插值過(guò)程中角速度不是恒定的。
歐拉角插值的前兩個(gè)問(wèn)題雖然煩人，但并不是不可克服的。限制歐拉角和將角度差限制在一定范圍內(nèi)提供了簡(jiǎn)單的解決方法。而對(duì)于萬(wàn)向鎖，非常不幸，它非常令人討厭，是一個(gè)底層的問(wèn)題。你可能會(huì)考慮重新規(guī)劃旋轉(zhuǎn)，發(fā)明一種不會(huì)遭遇這些問(wèn)題的系統(tǒng)。不幸的是，這不可能。這是一個(gè)用3個(gè)數(shù)表達(dá)3D方位的方法與生俱來(lái)的問(wèn)題。我們可以改變問(wèn)題，但不能消滅它們。任何使用三個(gè)數(shù)來(lái)表達(dá)3D方位的系統(tǒng)，若能保證空間的唯一性，就都會(huì)遇到這些問(wèn)題，如萬(wàn)向鎖。