什么是方位
直觀地說，我們知道物體的“方位”主要描述的是物體的朝向。然而“方向”和“方位”并不完全一樣。向量有“方向”但沒有“方位”，區(qū)別在于，當(dāng)一個向量指向特定方向時，可以讓向量自轉(zhuǎn)（如圖10.1所示），但向量（或者說它的方向）卻不會有任何變化，因?yàn)橄蛄康膶傩灾挥?#8220;大小”，而沒有“厚度”和“寬度”。
然而，當(dāng)一個物體朝向特定的方向時，讓它和上面的向量一樣自轉(zhuǎn)，你會發(fā)現(xiàn)物體的方位改變了，如圖10.2所示：
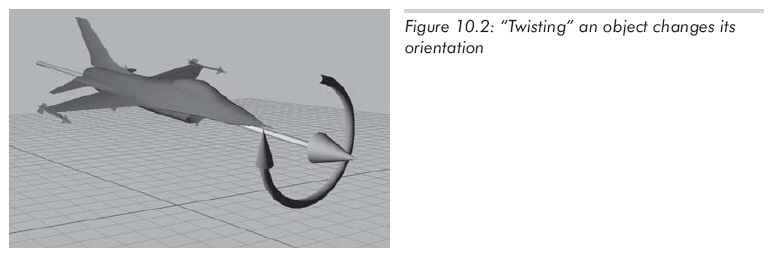
從技術(shù)角度來講，這就說明在3D中，只要用兩個數(shù)字（例如：極坐標(biāo)），就能用參數(shù)表示一個方向（direction）。但是，要確定一個方位（orientation），卻至少需要需要三個數(shù)字。
我們知道不能用絕對坐標(biāo)來描述物體的位置，要描述物體的位置，必須把物體放置于特定的參考系中。描述位置實(shí)際上就是描述相對于給定參考點(diǎn)（通常是坐標(biāo)系的原點(diǎn)）的位移。
同樣，描述物體方位時，也不能使用絕對量。與位置只是相對已知點(diǎn)的位移一樣，方位是通過與相對已知方位（通常稱為"單位"方位或"源"方位）的旋轉(zhuǎn)來描述的。旋轉(zhuǎn)的量稱作角位移。換句話說，在數(shù)學(xué)上描述方位就等價于描述角位移。
"方位"和"角位移"的區(qū)別就像"點(diǎn)"和"向量"的區(qū)別
----
兩個術(shù)語都只是在數(shù)學(xué)上等價而在概念上是不同的。方位和點(diǎn)主要用來描述一個單一的狀態(tài)，而角位移和向量描述的是兩個狀態(tài)間的差別。具體來說，我們用矩陣和四元數(shù)來表示"角位移"，用歐拉角來表示"
方位"。
矩陣形式
3D中，描述坐標(biāo)系中方位的一種方法就是列出這個坐標(biāo)系的基向量，這些基向量是用其他的坐標(biāo)系來描述的。用這些基向量構(gòu)成一個3x3矩陣，然后就能用矩陣形式來描述方位。換句話說，能用一個旋轉(zhuǎn)矩陣來描述這兩個坐標(biāo)系之間的相對方位，這個旋轉(zhuǎn)矩陣用于把一個坐標(biāo)系中的向量轉(zhuǎn)換到另外一個坐標(biāo)系中，如圖10.3所示：
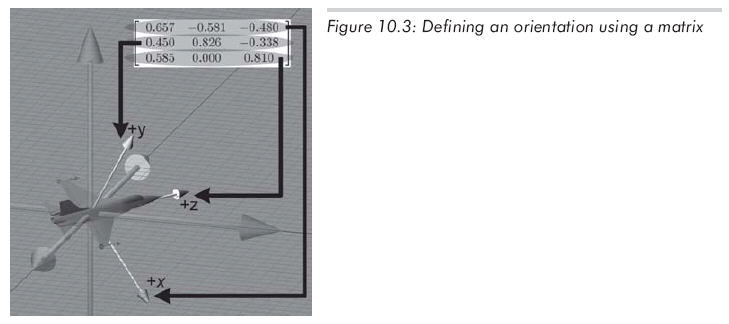
我們通過描述一個坐標(biāo)系到另一個坐標(biāo)系的旋轉(zhuǎn)（無論采用哪種變換）來確定一個方位。矩陣變換的具體方向是一個實(shí)現(xiàn)細(xì)節(jié)，因?yàn)樾D(zhuǎn)矩陣是正交的，如果必要的話，只需簡單的轉(zhuǎn)置就可求得逆變換。
矩陣形式的優(yōu)點(diǎn)
矩陣是一種非常直接的描述方位的形式，這種直接性帶來了如下優(yōu)點(diǎn)：
（1）可以立即進(jìn)行向量的旋轉(zhuǎn)。矩陣形式最重要的性質(zhì)就是利用矩陣能在物體和慣性坐標(biāo)系間旋轉(zhuǎn)向量，這是其他描述方位所做不到的。為了旋轉(zhuǎn)向量，必須將方位轉(zhuǎn)換成矩陣形式。
（2）矩陣形式被圖形API所采用。圖形API使用矩陣來描述方位。（API就是應(yīng)用程序接口，基本上它們就是實(shí)現(xiàn)你和顯卡交流的代碼。）當(dāng)你和圖形API交流時，最終必須用矩陣來描述所需的變換。程序中怎樣保存方位由你決定，但如果選擇了其他形式，則必須在渲染管道的某處將其轉(zhuǎn)換為矩陣。
（3）多個角位移連接。矩陣形式的第二個優(yōu)點(diǎn)就是可以 “打破”嵌套坐標(biāo)系間的關(guān)系。例如，如果知道A關(guān)于B的方位，又知道B關(guān)于C的方位，使用矩陣可以求得A關(guān)于C的方位。
（4）矩陣的逆。用矩陣形式表達(dá)角位移時，逆矩陣就是"反"
角位移。因?yàn)樾D(zhuǎn)矩陣是正交的，所以這個計算只是簡單的矩陣轉(zhuǎn)置運(yùn)算。
矩陣形式的缺點(diǎn)
（1）矩陣占用了更多的內(nèi)存。如果需要保存大量方位，如動畫序列中的關(guān)鍵幀，9個數(shù)會導(dǎo)致數(shù)目可觀的額外空間損失。舉一個或許不太合適的例子，假設(shè)現(xiàn)在做的是一個人的模型動畫，該模型被分解為15塊。動畫的完成實(shí)際是嚴(yán)格地控制子塊和父塊之間的相對方位。假設(shè)每一幀為每一塊保存一個方位，動畫頻率是15HZ
，這意味這每秒需要保存225個方位。使用矩陣和32位浮點(diǎn)數(shù)，每一幀有8100字節(jié)，而使用歐拉角，同樣的數(shù)據(jù)只需2700字節(jié)。對于30s的動畫數(shù)據(jù)，矩陣就比歐拉角多占用162k字節(jié)。
（2）難以使用。矩陣對人類來說并不直觀，有太多的數(shù)，并且它們都在-1到1之間。人類考慮方位的直觀方法是角度，而矩陣使用的是向量。通過實(shí)踐，我們能從一個給定的矩陣中得到它所表示的方位。但這仍比歐拉角困難得多，其他方面也不盡如人意。用手算來構(gòu)造描述任意方位的矩陣幾乎是不可能的。總之，矩陣不是人類思考方位的直觀方法。
（3）矩陣可能是病態(tài)的。矩陣使用9個數(shù)，其實(shí)只有3個數(shù)是必須的。也就是說，矩陣帶有6階冗余。描述方位的矩陣必須滿足6個限制條件。行必須是單位向量，而且它們互相垂直。
病態(tài)矩陣是怎樣出現(xiàn)的呢？有多種原因：
1、矩陣可能包含縮放、切變或鏡像操作，這些操作會對物體的"方位"產(chǎn)生什么影響呢？確實(shí)，對此沒有一個清晰的定義。任何非正交的矩陣都不是一個定義良好的旋轉(zhuǎn)矩陣。雖然鏡像矩陣也是正交的，但它不是有效的旋轉(zhuǎn)矩陣。
2、可能從外部數(shù)據(jù)源獲得"壞"數(shù)據(jù)。例如，使用物體數(shù)據(jù)獲取設(shè)備（如動作捕捉器）時，捕獲過程中可能產(chǎn)生錯誤。許多建模包就是因?yàn)闀a(chǎn)生病態(tài)矩陣而變得聲名狼藉。
3、可能因?yàn)楦↑c(diǎn)數(shù)的舍入錯誤產(chǎn)生"壞"數(shù)據(jù)。例如，對一個方位作大量的加運(yùn)算，這在允許人們手動控制物體方位的游戲中是很常見的。由于浮點(diǎn)精度的限制，大量的矩陣乘法最終可能導(dǎo)致病態(tài)矩陣，這種現(xiàn)象稱作"矩陣蠕變"。