一般仿射變換
3x3矩陣僅能表達3D中的線性變換,不能包含平移。經過4x4矩陣的武裝后,現在我們可以構造包含平移在內的一般仿射變換矩陣了。例如:
(1)繞不通過原點的軸旋轉。
(2)沿不穿過原點的平面縮放。
(3)沿不穿過原點的平面鏡像。
(4)向不穿過原點的平面正交投影。
它們的基本思想是將變換的"中心點"平移到原點,接著進行線性變換,然后再將"中心點"平移回原來的位置。開始使用平移矩陣T將點P移到原點,接著用線性變換矩陣R進行線性變換,最終的仿射變換矩陣M等于矩陣的積,即:TRT-1。T-1是平移矩陣,執行和T相反的變換。
觀察這種矩陣的一般形式,它非常有趣。讓我們先用 "分塊"形式寫出前面用到的T、R、T-1。

可以看出,仿射變換中增加的平移部分僅僅改變了4x4矩陣的最后一行,并沒有影響到上面所包含的線性變換的3x3部分。
透視投影
學習透視投影最好的方法是將它和平行投影相比較。正交投影也稱作平行投影,因為投影線都是平行的(投影線是指從原空間中的點到投影點的連線)。正交投影中的平行線如圖9.3所示:
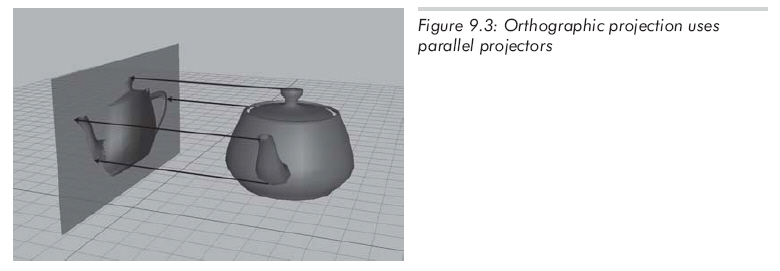
3D中的透視投影仍然是投影到2D平面上,但是投影線不再平行,實際上,它們相交于一點,該點稱作投影中心。如圖9.4所示:
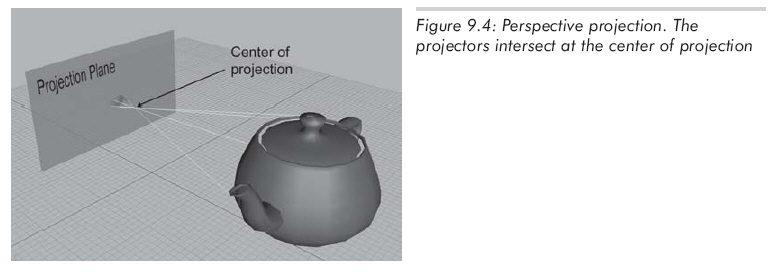
因為投影中心在投影平面前面,投影線到達平面之前已經相交,所以投影平面上的圖像是翻轉的。當物體遠離投影中心時,正交投影仍保持不變,但透視投影變小了。如圖9.5所示:

圖9.5中,右邊的茶壺離投影平面更遠,所以它的投影比離投影平面較近的那個茶壺小。這是一種非常重要的視覺現象,稱作透視縮略。
小孔成像
透視投影在圖形學中非常重要,因為它是人類視覺系統的模型。實際上,人類視覺系統遠比這復雜,因為我們有兩只眼睛,而且對于每只眼睛,投影表面(視網膜)不是一個平面。所以,讓我們來看一個簡單些的例子----小孔成像。小孔成像系統就是一個盒子,一側上有小孔,光線穿過小孔照射到另一側的背面,那里就是投影平面。如圖9.6所示:
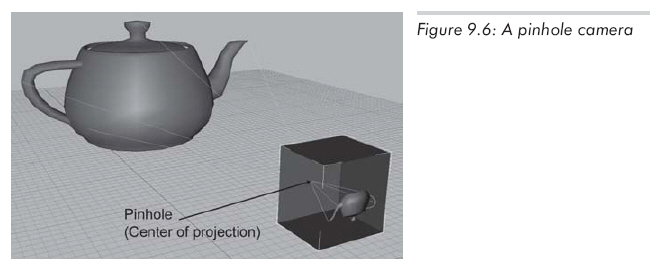
圖9.6中,盒子左面和右面是透明的,以使你能看見盒子內部。注意盒子內部的投影是倒著的,這是因為光線(投影線)已經在小孔處(投影中心)相交了。
讓我們探索小孔成像背后的幾何原理。設想一個3D坐標系,它的原點在投影中心,z軸垂直于投影平面,x和y軸平行于投影平面。如圖9.7所示:
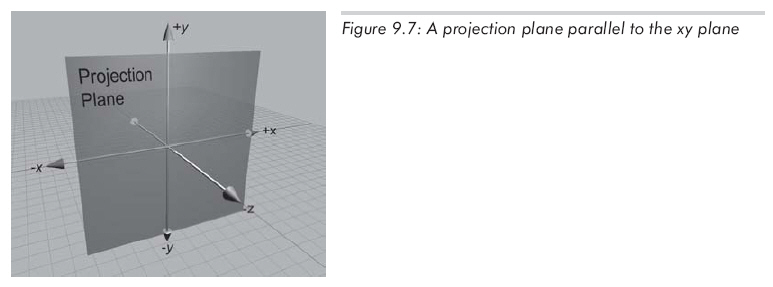
讓我們看看能否計算出任意點p通過小孔投影到投影平面上的坐標p'。首先,需要知道小孔到投影平面的距離,設為d。因此,投影平面為z=-d。現在,從另一個角度來看問題,求出新的y。如圖9.8所示。
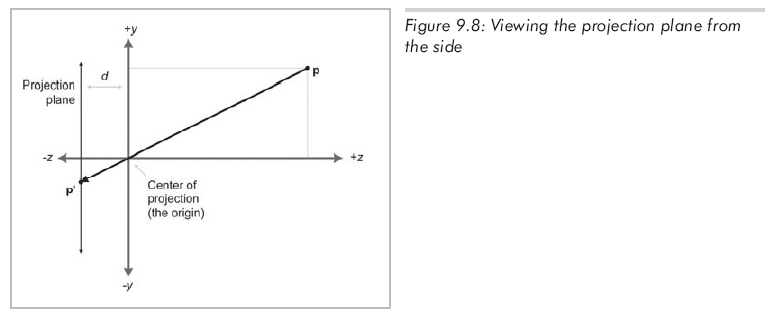
由相似三角形得到:
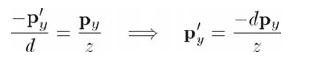
注意小孔成像顛倒了圖像,py和py'的符號相反。px'的值可通過類似的方法求得:
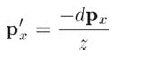
所有投影點的z值都是相同的:-d。因此,點p通過原點向平面z=-d投影的結果如公式9.11所示:
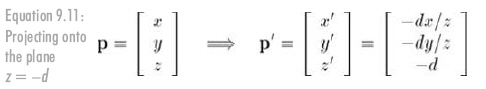
在實際應用中,負號會帶來不必要的復雜性。所以將投影平面移到投影的前面(也就是說,平面z=d),如圖 9.9所示:

當然,這對于實際的小孔成像是不可能的。因為設置小孔的目的就是使光線只能通過小孔,但在計算機數學世界中,可以不理會這些規定。如你所愿,將投影平面移到投影中心前面,煩人的負號消失了,如公式9.12所示:
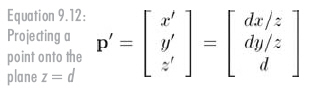
使用4x4矩陣進行透視投影
從4D到3D的變換就意味著除法運算,因此我們可以利用4x4階矩陣來編寫代碼,以實現透視投影。基本思想是提出一個關于p'的公式,其中的x、y、z有公分母,然后構造一個4x4矩陣,使w與這個公分母相等。這里我們假設初始點處有w=1。
先對3D形式表達的p'公式變形,可以得到:
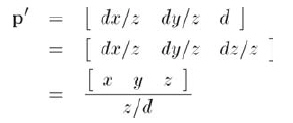
將4D齊次向量變換到3D時,要用4D向量除以w,反推可知p'的4D形式為:
[x y z z/d]
因此我們需要一個4x4矩陣,它可接收一個奇異的齊次向量。該向量的形式為[x,
y, z, 1],然后將其變換為上述形式。這樣的矩陣如公式9.13所示:

這樣就得到了一個4x4投影矩陣,有幾個需要注意的地方:
(1)乘以這個矩陣并沒有進行實際的透視投影變換,它只是計算出合適的分母。投影實際發生在從4D向3D變換時。
(2)存在多種變換。例如,將投影平面放在z=0處而投影中心在[0,
0, -d],這將導致一個不同的公式。
(3)這里看起來比較復雜,似乎只需要簡單地除以z,不必勞煩矩陣。那么為什么要使用齊次矩陣呢?第一,4x4矩陣提供了一個方法將投影表達為變換,這樣就能和其他變換相連接;第二,使得投影到不平行于坐標軸的平面變得可行。實際上,我們不需要齊次坐標做任何運算,但4x4矩陣提供了一種簡潔的方法表達和操縱投影變換。
(4)實際的圖形幾何管道中的投影矩陣不像這里導出的那樣,還有許多重要的細節需要考慮。如用以上矩陣對向量進行變換后,z值實際上被舍棄了,而很多圖形系統的z緩沖用到了該值。