正交矩陣的運(yùn)算法則
若方陣M是正交的，則當(dāng)且僅當(dāng)M與它轉(zhuǎn)置矩陣MT的乘積等于單位矩陣，見(jiàn)公式9.8：
矩陣乘以它的逆等于單位矩陣：M M-1 = I
所以，如果一個(gè)矩陣是正交的，那么它的轉(zhuǎn)置等于它的逆：
這是一條非常有用的性質(zhì)，因?yàn)樵趯?shí)際應(yīng)用中經(jīng)常需要計(jì)算矩陣的逆，而3D圖形計(jì)算中正交矩陣出現(xiàn)又是如此頻繁。比如旋轉(zhuǎn)和鏡像矩陣是正交的，如果知道矩陣是正交的，就可以完全避免計(jì)算逆矩陣了，這也將大大減少計(jì)算量。
正交矩陣的幾何解釋
正交矩陣對(duì)我們非常有用，因?yàn)楹苋菀子?jì)算它的逆矩陣。但怎樣知道一個(gè)矩陣是否正交，以利用它的性質(zhì)呢？
很多情況下，我們可以提前知道矩陣是如何建立的，甚至了解矩陣是僅包含旋轉(zhuǎn)、鏡像呢，還是二者皆有（記住：旋轉(zhuǎn)和鏡像矩陣是正交的）。這種情況非常普遍。
如果無(wú)法提前清楚矩陣的某些情況呢？換句話說(shuō)，對(duì)于任意矩陣M，怎樣檢測(cè)它是否正交？為了做到這一點(diǎn)，讓我們從正交矩陣的定義開(kāi)始，以3x3階矩陣為例。設(shè)M是3x3矩陣，根據(jù)定義，當(dāng)且僅當(dāng)
M MT = I 時(shí)M是正交的。它的確切含義如下：
現(xiàn)在做一些解釋：
（1）當(dāng)且僅當(dāng)一個(gè)向量是單位向量時(shí)，它與自身的點(diǎn)積結(jié)果是1。因此，僅當(dāng)r1、r2、r3是單位向量時(shí)，第1、5、9式才能成立。
（2）當(dāng)且僅當(dāng)兩個(gè)向量是互相垂直時(shí)，它們的點(diǎn)積為0。因此，僅當(dāng)r1、r2、r3互相垂直時(shí)其他等式才成立。
所以，若一個(gè)矩陣是正交的，它必須滿足下列條件：
矩陣的每一行都是單位向量，矩陣的所有行互相垂直。
對(duì)矩陣的列也能得到類似的條件，這使得以下結(jié)論非常清楚：如果M是正交的，則MT也是正交的。
計(jì)算逆矩陣時(shí)，僅在預(yù)先知道矩陣是正交的情況下才能利用正交性的優(yōu)點(diǎn)。如果預(yù)先不知道，那么檢查正交性經(jīng)常是浪費(fèi)時(shí)間。即使在最好的情況下，先檢查正交性以確定矩陣是否正交再進(jìn)行轉(zhuǎn)置，和一開(kāi)始就進(jìn)行求逆運(yùn)算也將耗費(fèi)同樣多的時(shí)間。而如果矩陣不是正交，那么這種檢查完全是浪費(fèi)時(shí)間。
注意，有一個(gè)術(shù)語(yǔ)上的差別可能會(huì)導(dǎo)致輕微的混淆。線性代數(shù)中，如果一組向量互相垂直，這組向量就被認(rèn)為是正交基（orthogonal
basis）。它只要求所有向量互相垂直，并不要求所有向量都是單位向量。如果它們都是單位向量，則稱它們?yōu)闃?biāo)準(zhǔn)正交基（orthogonal
basis）。這里所講的正交矩陣的行或列向量都是指標(biāo)準(zhǔn)正交基向量（orthogonal basis
vectors），所以由一組正交基向量構(gòu)造的矩陣并不一定是正交矩陣（除非基向量是標(biāo)準(zhǔn)正交的）。
矩陣正交化
有時(shí)可能會(huì)遇到略微違反了正交性的矩陣。例如，可能從外部得到了壞數(shù)據(jù)，或者是浮點(diǎn)運(yùn)算的累積錯(cuò)誤（稱作”矩陣爬行“）。這些情況下，需要做矩陣正交化，得到一個(gè)正交矩陣，這個(gè)矩陣要盡可能地和原矩陣相同（至少希望是這樣）。
構(gòu)造一組正交基向量（矩陣的行）的標(biāo)準(zhǔn)算法是施密特正交化。它的基本思想是，對(duì)每一行，從中減去它平行于已處理過(guò)的行的部分，最后得到垂直向量。
以3x3矩陣為例，和以前一樣，用r1、r2、r3代表3x3階矩陣M的行。正交向量組r1'、r2'、r3'的計(jì)算如公式9.9所示：
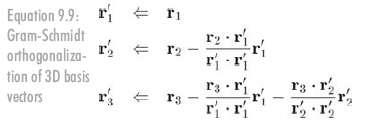
現(xiàn)在r1'、r2'、r3'互相垂直了，它們是一組正交基。當(dāng)然，它們不一定是單位向量。構(gòu)造正交矩陣需要使用標(biāo)準(zhǔn)正交基，所以必須標(biāo)準(zhǔn)化這些向量。注意，如果一開(kāi)始就進(jìn)行標(biāo)準(zhǔn)化，而不是在第2步中做，就能避免所有除法了。
施密特正交化是有偏差的，這取決于基向量列出的順序。一個(gè)明顯的例子是，r1總不用改變。該算法的一個(gè)改進(jìn)是不在一次正交化過(guò)程中將整個(gè)矩陣完全正交化。而是選擇一個(gè)小的因子k，每次只減去投影的k倍，而不是一次將投影全部減去。改進(jìn)還體現(xiàn)在，在最初的軸上也減去投影。這種方法避免了因?yàn)檫\(yùn)算順序不同帶來(lái)的誤差。算法總結(jié)如下:
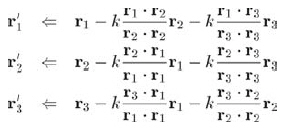
該算法的每次迭代都會(huì)使這些基向量比原來(lái)的基向量更為正交化，但可能不是完全正交的，多次重復(fù)這個(gè)過(guò)程，最終將得到一組正交基。要得到完美的結(jié)果，就得選擇一個(gè)適當(dāng)?shù)囊蜃觡并迭代足夠多次（如：10次）。接著，進(jìn)行標(biāo)準(zhǔn)化，最后就會(huì)得到一組正交基。