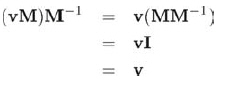3D數學 ---- 矩陣的更多知識(2)
矩陣的逆
另外一種重要的矩陣運算是矩陣的求逆,這個運算只能用于方陣。
運算法則
方陣M的逆,記作M-1,也是一個矩陣。當M與M-1相乘時,結果是單位矩陣。表示為公式9.6的形式:
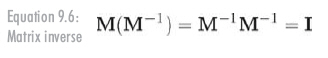
并非所有的矩陣都有逆。一個明顯的例子是若矩陣的某一行或列上的元素都為0,用任何矩陣乘以該矩陣,結果都是一個零矩陣。如果一個矩陣有逆矩陣,那么稱它為可逆的或非奇異的。如果一個矩陣沒有逆矩陣,則稱它為不可逆的或奇異矩陣。奇異矩陣的行列式為0,非奇異矩陣的行列式不為0,所以檢測行列式的值是判斷矩陣是否可逆的有效方法。此外,對于任意可逆矩陣M,當且僅當v=0時,vM=0。
M的”標準伴隨矩陣“記作”adjM“,定義為M的代數余子式矩陣的轉置矩陣。下面是一個例子,考慮前面給出的3x3階矩陣M:
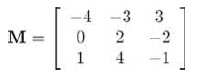
計算M的代數余子式矩陣:
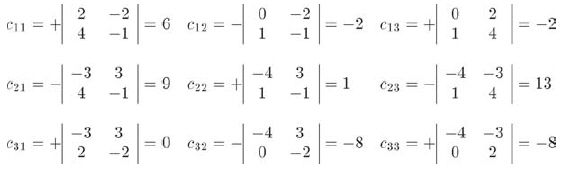
M的標準伴隨矩陣是代數余子式矩陣的轉置:
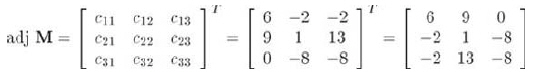
一旦有了標準伴隨矩陣,通過除以M的行列式,就能計算矩陣的逆。
其表示如公式9.7所示:

例如為了求得上面矩陣的逆,有:
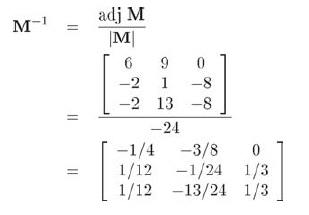
當然還有其他方法可以用來計算矩陣的逆,比如高斯消元法。很多線性代數書都斷定該方法更適合在計算機上實現,因為它所使用的代數運算較少,這種說法其實是不正確的。對于大矩陣或某些特殊矩陣來說,這也許是對的。然而,對于低階矩陣,比如幾何應用中常見的那些低階矩陣,標準伴隨矩陣可能更快一些。因為可以為標準伴隨矩陣提供無分支(branchless)實現,這種實現方法在當今的超標量體系結構和專用向量處理器上會更快一些。
矩陣的逆的重要性質:

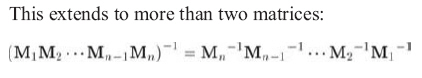
幾何解釋
矩陣的逆在幾何上非常有用,因為它使得我們可以計算變換的”反向“或”相反“變換 ---- 能”撤銷“原變換的變換。所以,如果向量v用矩陣M來進行變換,接著用M的逆M-1進行變換,將會得到原向量。這很容易通過代數方法驗證: