矩陣的行列式
在任意方陣中都存在一個標量,稱作該方陣的行列式。
線性運算法則
方陣M的行列式記作|M|或“det
M”,非方陣矩陣的行列式是未定義的。n x n階矩陣的行列式定義非常復雜,讓我們先從2
x 2,3 x 3矩陣開始。
公式9.1給出了2 x 2階矩陣行列式的定義:
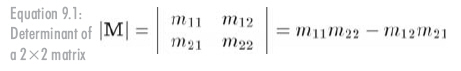
注意,在書寫行列式時,兩邊用豎線將數字塊圍起來,省略方括號。
下面的示意圖能幫助記憶公式9.1,將主對角線和反對角線上的元素各自相乘,然后用主對角線元素的積減去反對角線元素的積。
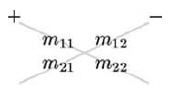
3 x 3 階矩陣的行列式定義如公式9.2所示:
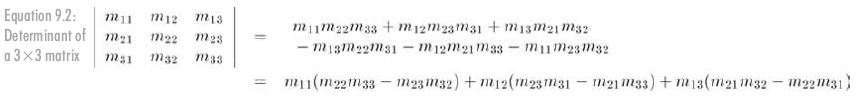
可以用類似的示意圖來幫助記憶。把矩陣M連寫兩遍,將主對角線上的元素和反對角線上的元素各自相乘,然后用各主對角線上元素積的和減去各反對角線上元素積的和。
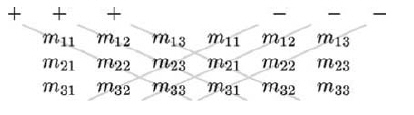
如果將3 x 3階矩陣的行解釋為3個向量,那么矩陣的行列式等于這些向量的所謂“三元組積”。
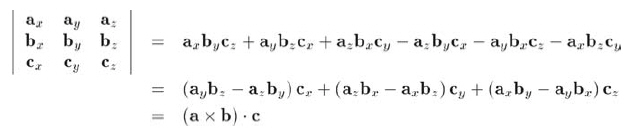
假設矩陣M有r行c列,記法M{ij}表示從M中除去第i行和第j列后剩下的矩陣。顯然,該矩陣有r-1行,c-1列,矩陣M{ij}稱作M的余子式。
對方陣M,給定行、列元素的代數余子式等于相應余子式的有符號行列式,見公式9.3:
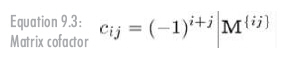
如上,用記法cij表示M的第i行,第j列元素的代數余子式。注意余子式是一個矩陣,而代數余子式是一個標量。代數余子式計算式中的項(–1)(i+j)有以棋盤形式使矩陣的代數余子式每隔一個為負的效果:

n維方陣的行列式存在著多個相等的定義,我們可以用代數余子式來定義矩陣的行列式(這種定義是遞歸的,因為代數余子式本身的定義就用到了矩陣的行列式)。
首先,從矩陣中任意選擇一行或一列,對該行或列中的每個元素,都乘以對應的代數余子式。這些乘積的和就是矩陣的行列式。例如,任意選擇一行,如行i,行列式的計算過程如公式9.4所示:
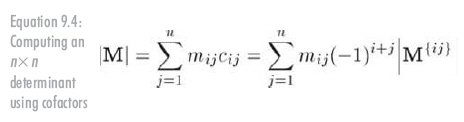
下面舉一個例子,重寫3x3矩陣的行列式:
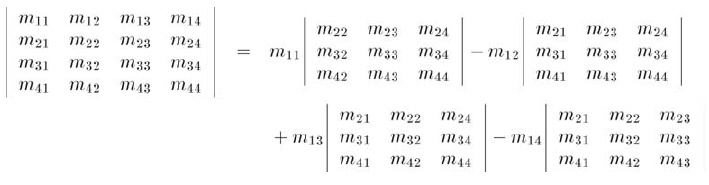
綜上,可導出4x4矩陣的行列式:
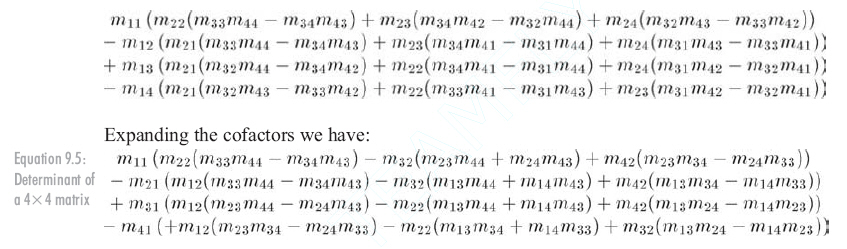
高階行列式計算的復雜性是呈指數遞增的。幸運的是,有一種稱作”主元選擇“的計算方法,它不影響行列式的值,但它能使特定的行或列中除了一個元素(主元)外其他元素全為0,這樣僅一個代數余子式需要計算。
行列式的一些重要性質:
(1)矩陣積的行列式等于矩陣行列式的積:|AB| = |A||B|
這可以擴展到多個矩陣:
|M1 M2 ... Mn| = |M1| |M2| ... |Mn-1| |Mn|
(2)矩陣轉置的行列式等于原矩陣的行列式:|MT| = |M|
(3)如果矩陣的任意行或列全為0,那么它的行列式等于0.
(4)交換矩陣的任意兩行或兩列,行列式變負。
(5)任意行或列的非零積加到另一行或列上不會改變行列式的積。
幾何解釋
矩陣的行列式有著非常有趣的幾何解釋。2D中,行列式等于以基向量為兩邊的平行四邊形的有符號面積(如圖9.1所示)。有符號面積是指如果平行四邊形相對于原來的方位”翻轉“,那么面積變負。
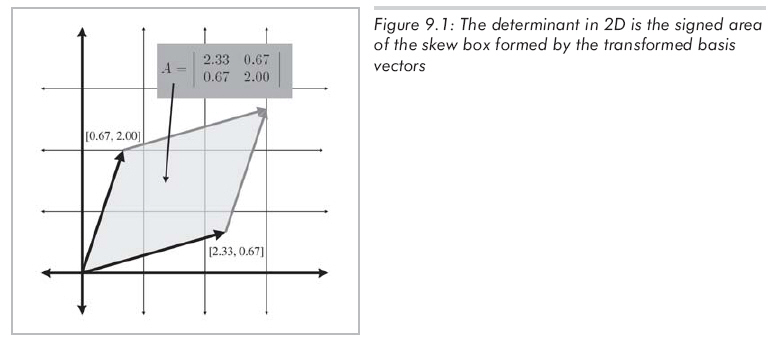
3D中,行列式等于以變換后的基向量為三邊的平行六面體的有符號的體積。3D中,如果變換使得平行六面體”有里向外“翻轉,則行列式變負。
行列式與矩陣變換導致的尺寸改變相關,其中行列式的絕對值與面積(2D)、體積(3D)的改變相關,行列式的符號說明了變換矩陣是否包含鏡像或投影。
矩陣的行列式還能對矩陣所代表的變換進行分類。如果矩陣的行列式為0,那么該矩陣包含投影。如果矩陣的行列式為負,那么該矩陣包含鏡像。