變換的組合
設想世界中有一個任意方向、任意位置的物體,我們要把它渲染到任意方向、任意位置的攝像機中。為了做到這一點,必須將物體的所有頂點從物體坐標系變換到世界坐標系,接著再從世界坐標系變換到攝像機坐標系。其中的數學變換總結如下:

矩陣乘法滿足結合律,所以我們能用一個矩陣直接從物體坐標系變換到攝像機坐標系:
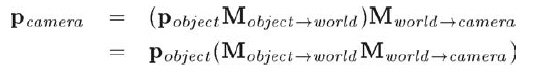
這樣就能在渲染的循環外先將所有矩陣組合起來,使循環內作矩陣乘法的時候只需要和一個矩陣相乘即可(物體有很多頂點,省一次矩陣乘法就會提高不少效率),如下:

所以矩陣組合從代數角度看是利用了矩陣乘法的結合律。矩陣的行向量就是變換后的基向量,這在多個變換的情況下也是成立的。考慮矩陣乘法AB,結果中的每一行都是A中相應的行與矩陣B相乘的結果。換言之,設a1,
a2, a3為A的行,矩陣乘法能夠寫為:
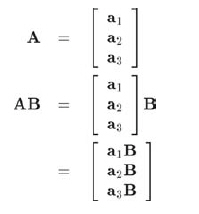
這使得結論更加清晰,AB結果中的行向量確實是對A的基向量進行B變換的結果。
變換分類
變換的類別并不是互斥的,也不存在一定的“次序”或“層次”使得某一類比另一類多或少一些限制。
當討論一般意義上的變換時,我們將使用類似的術語:映射或函數。在最一般的意義上,映射就是一種簡單的規則,接受輸入,產生輸出。我們把從a到b的F映射記作F(a)
= b。
線性變換
在數學上,如果滿足下式,那么映射F(a)就是線性的:
F(a + b) = F(a) + F(b) 以及
F(ka) = kF(a)
如果映射F保持了基本運算:加法和數量乘,那么就可以稱該映射為線性的。在這種情況下,將兩個向量相加然后再進行變換得到的結果和先分別進行變換再將變換后的向量相加得到的結果相同。同樣,將一個向量數量乘再進行變換和先進行變換再數量乘的結果也是一樣的。
這個線性變換的定義有兩條重要的引理:
(1) 映射F(a)
= aM,當M為任意方陣時,說映射是一個線性變換,這是因為:
F(a + b) = (a + b)M
= aM + bM = F(a) + F(b)
和
F(ka) = (ka)M = k(aM) =
kF(a)
(2) 零向量的任意線性變換的結果仍然是零向量。(如果F(0)
= a,a ≠ 0。那么F不可能是線性變換。因為F(k0)
= a,但F(k0) ≠ kF(0)),因此線性變換不會導致平移(原點位置上不會變化)。
在某些文獻中,線性變換的定義是平行線變換后仍然是平行線。大多數情況下它是對的,但有一個小小的例外:投影(當一條直線投影后變成一個點,能認為這個點平行于什么?)除了這點理論上的例外,這種定義是正確的。線性變換可能造成“拉伸”,但直線不會”彎折“,所以平行線仍然保持平行。
仿射變換
仿射變換是指線性變換后接著平移。因此仿射變換的集合是線性變換的超集,任何線性變換都是仿射變換,但不是所有仿射變換都是線性變換。
任何具有形式 v' = vM + b 的變換都是仿射變換。
可逆變換
如果存在一個逆變換可以”撤銷“原變換,那么該變換是可逆的。換句話說,如果存在逆變換G,使得G(F(a))
= a,對于任意a,映射F(a)是可逆的。
存在非仿射變換的可逆變換,但暫不考慮它們。現在,我們集中精力于檢測一個仿射變換是否可逆。一個仿射變換就是一個線性變換加上平移,顯然,可以用相反的量”撤銷“平移部分,所以問題變為一個線性變換是否可逆。
顯然,除了投影以外,其他變換都能”撤銷“。當物體被投影時,某一維有用的信息被拋棄了,而這些信息時不可能恢復的。因此,所有基本變換除了投影都是可逆的。
因為任意線性變換都能表達為矩陣,所以求逆變換等價于求矩陣的逆。如果矩陣是奇異的,則變換不可逆;可逆矩陣的行列式不為0。
等角變換
如果變換前后兩向量夾角的大小和方向都不改變,該變換是等角的。只有平移,旋轉和均勻縮放是等角變換。等角變換將會保持比例不變,鏡像并不是等角變換,因為盡管兩向量夾角的大小不變,但夾角的方向改變了。所有等角變換都是仿射和可逆的。
正交變換
術語“正交”用來描述具有某種性質的矩陣。正交變換的基本思想是軸保持互相垂直,而且不進行縮放變換。
平移、旋轉和鏡像是僅有的正交變換。長度、角度、面積和體積都保持不變。(盡管如此,但因為鏡像變換被認為是正交變換,所以一定要密切注意角度、面積和體積的準確定義)。
正交矩陣的行列式為1或者負1,所有正交矩陣都是仿射和可逆的。
剛體變換
剛體變換只改變物體的位置和方向,不包括形狀。所有長度、角度、面積和體積都不變。平移和旋轉是僅有的剛體變換,鏡像并不被認為是剛體變換。剛體變換也被稱作正規變換,所有剛體變換都是正交、等角、可逆和仿射的,某些剛體變換旋轉矩陣的行列式為1。