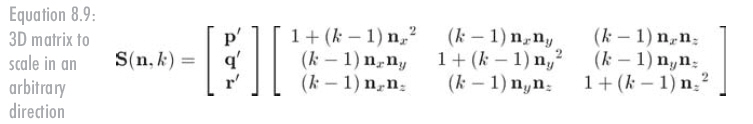我們可以通過讓比例因子k按比例放大或縮小來縮放物體。如果在各方向應(yīng)用同比例的縮放，并且沿原點“膨脹”物體，那么就是均勻縮放。均勻縮放可以保持物體的角度和比例不變。如果長度增加或減小因子k，則面積增加或減小k^2。在3D中，體積將增加或減小 k^3。

如果需要“擠壓”或"拉伸"物體，在不同的方向應(yīng)用不同的因子即可，這稱作非均勻縮放。非均勻縮放時，物體角度將發(fā)生變化。視各方向縮放因子的不同，長度、面積、體積的變化因子也各不相同。

如果|k|<1，物體將“變短”；如果|k|>1，物體將“變長”，如果k = 0，就是正交投影，如果k < 0就是鏡像。

應(yīng)用非均勻縮放的效果類似于切變，事實上，非均勻縮放和切變是很難區(qū)分的。

沿坐標軸的縮放

最簡單的縮放方法是沿著每個坐標軸應(yīng)用單獨的縮放因子，縮放是沿著垂直的軸（2D中）或平面（3D中）進行的。如果每個軸的縮放因子相同，就是均勻縮放，否則是非均勻縮放。

2D中有兩個不同的縮放因子，Kx和Ky，圖8.13展示了應(yīng)用不同縮放因子后的情況。

憑直覺就可知道，基向量p，q由相應(yīng)的縮放因子單獨影響：

p' = Kxp = Kx [1   0] = [Kx   0]

q' = Kyq = Ky [0   1] = [0   Ky]

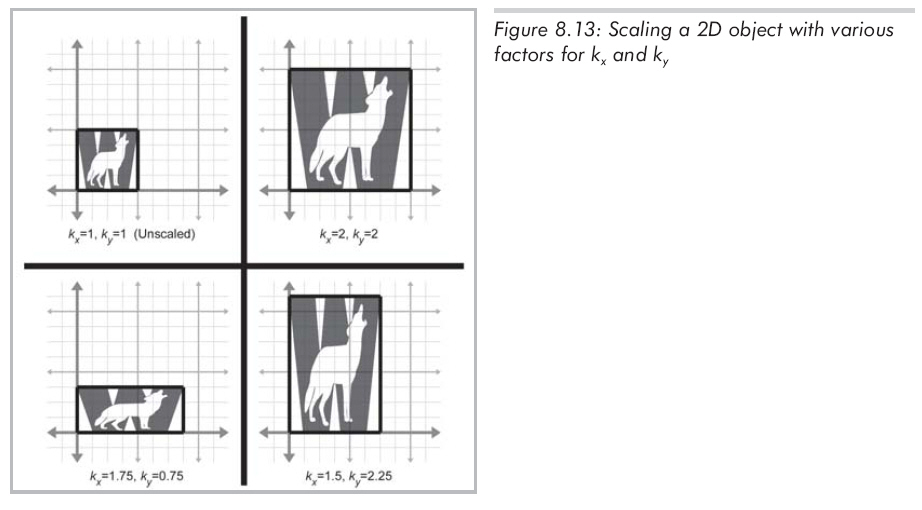
用基向量構(gòu)造矩陣，結(jié)果如公式8.6所示：

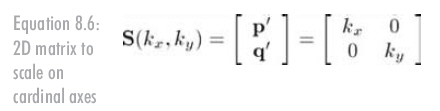
對于3D，需要增加第三個縮放因子Kz，3D縮放矩陣如公式8.7所示：

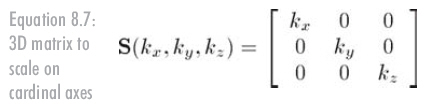
沿任意方向縮放

我們可以不依賴于坐標系而沿任意方向進行縮放，設(shè)n為平行于縮放方向的單位向量，k為縮放因子，縮放沿穿過原點并平行于n的直線（2D中）或平面（3D中）進行。

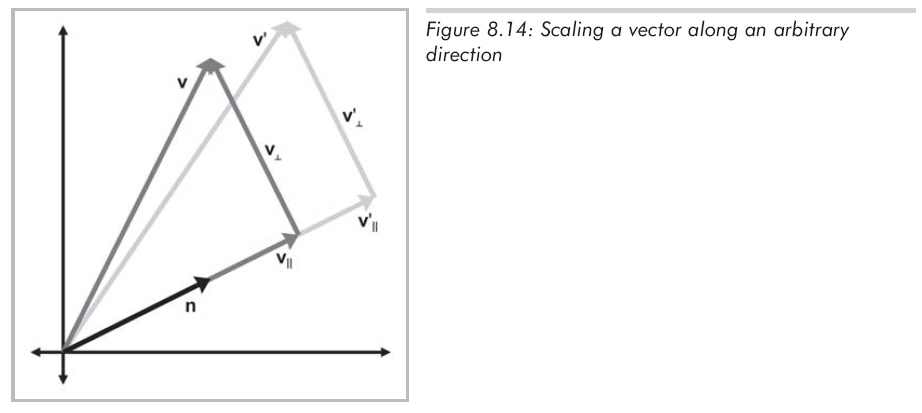
我們需要推導出一個表達式，給定向量v，可以通過v，n和k來計算v'。為了做到這一點，將v分解為兩個分量，v||和v⊥，分別平行于n和垂直于n，并滿足v =v|| + v⊥。v||是v在n上的投影，由 (v . n)n 可以得到 v||。因為v⊥垂直于n，它不會被縮放操作影響。因此，v' = v||' + v⊥，剩下的問題就是怎樣得到v||'。由于v||平行于縮放方向，v||'可以由公式kv||得出，如圖8.14所示：

總結(jié)已知向量并進行代換，得到：

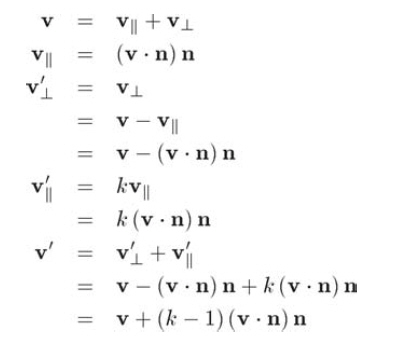
既然我們知道了怎樣對任意向量進行縮放，當然也就可以計算縮放后的基向量。這里只詳細列出2D中的一個基向量的求法，其余的基向量依次類推。我們只給出其結(jié)果（注意下面采用列向量形式只是為了使等式的形式好看一些。）

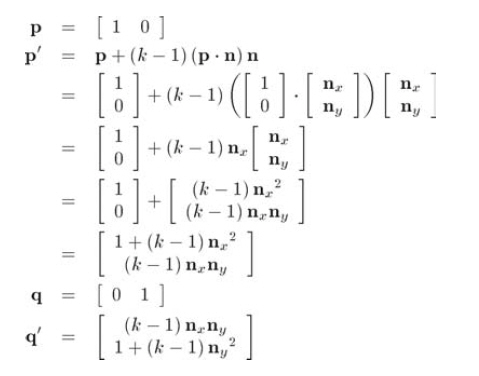
通過基向量構(gòu)造矩陣，得到以單位向量n為縮放方向，k為因子的縮放矩陣，如公式8.8所示：

3D中，基向量為：

以單位向量n為縮放方向，k為因子的3D縮放矩陣如公式8.9所示：