通過這篇文章我們主要回答以下幾個問題:
1. LSH解決問題的背景,即以圖片相似性搜索為例,如何解決在海量數據中進行相似性查找?
2. 圖像相似性查找的連帶問題:相似性度量,特征提取;
3. LSH的數學分析,即局部敏感HASH函數的數學原理,通過與、或構造提升查找的查全率與查準率
4. LSH具體實現,對著代碼一步一步學習算法的具體實現
一、問題背景介紹
LSH即Locality Sensitive hash,用來解決在海量數據中進行相似性查找的問題,以圖片搜索為例,見下圖,用戶向百度圖搜提交待搜索圖片,百度圖搜將相似的圖片返回展示。

要實現這樣一個應用,需要考慮以下幾個問題:
1. 提取用戶提交的圖片特征,即將提交圖片轉換成一個特征向量;
2. 預先將所有收集到的圖片進行特征提取;
3. 把步驟1中提取的特征與步驟2中的特征集合,進行比對,并記錄比對的相似性值;
4. 對相似值由大到小排序,返回相似度最高的作為檢索結果。
問題1,2是一個圖片特征提取的問題,與LSH無關。LSH主要解決問題3與問題4,在海量特征集中找到相似特征。以下簡述問題1,2,詳細講解問題3,4。
二、圖像的特征提取
圖像的特征提取屬于個圖像學研究領域,有很多經典的圖像算法,分別從圖像顏色,角度,形態不同角度進行圖像的特征描述,包括最近流行的深度學習方法也可以做類似的事情。這里介紹一種比較容易理解的2種方法,一種是傳統的顏色直方圖,一種是自編碼器。
1. 顏色直方圖就是將RGB圖像中出現的顏色進行統計,將一張圖像描述中一個256維度的特征向量,如下圖所示:

2. 自編碼器的思想是通過神經網絡進行特征提取,提取出針對學習樣本的通用特征降維方法,用訓練得到的統一方法對待測圖像進行降維處理,得到一個特征向量。
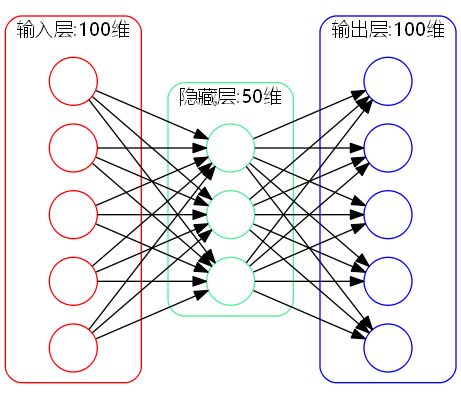
如圖所示,神經網絡的2端通過相同的數據限制,學習到中間的隱藏層權重,通過使用降維再升維的方法,使隱藏層輸出最大限度的保存圖像的主要特征,以使還原后的圖像與原圖像誤差達到最小。
自編碼器完成訓練后,使用輸入層到隱藏層的權重向量進行特征提取,將圖像數據作為輸入層輸入,將隱藏層輸出作為圖像特征,以此作為圖像的特征。
三、特征的相似性比較
相似是一個形容詞,對于一對圖像使用不同的評價標準可能得到不同相似度量值。比如對于不同的業務場景,如相貌識別、形態識別、背景識別所采用相似度量方法可能完全是不同的。
同樣從數學的角度進行特征的相似性比較也有不同的方法,如果把特征向量看成空間的一個點,那么可以把度量2個向量的相似性看做度量多維空間中的2個點的距離,這些度量方法包括:
歐式距離
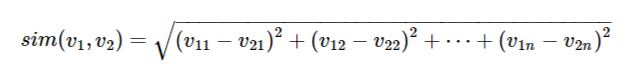
Jaccard距離
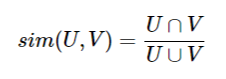
余弦距離
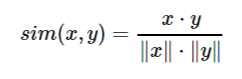
曼哈頓距離
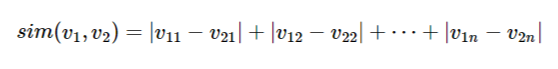
閔可夫斯基距離
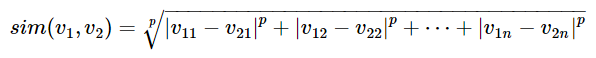
作為一個距離的度量函數d,必須滿足以下一些性質
• d(x,y)>=0,距離非負性
• d(x,y)=0當切僅當x=y,只有點到自身的距離為0,其他距離都大于0
• d(x,y)=d(y,x),距離對稱性
• d(x,y)<=d(x,z)+d(z,y),滿足三角不等式
當完成了第1,第2步以后,即能提取圖像的特征,又找到了方法可以度量圖像特征的相似后,剩下的事情就是要預先將圖像庫的所有圖像一一提取特征,在搜索時用同樣的特征提取方法對待測圖像提取特征,然后將待搜特征循環與圖像庫中的圖像特征集合比較,找到相似度最高的。
四、局部敏感hash
由于圖像庫的特征通常數量很大,循環比較的時間復雜度過高,無法滿足應用的響應需要。因此,必須要使用類似的索引技術來降低搜索的復雜性,多維索引有一種叫KD樹的技術可以做類似的事情,但是對于圖像搜索的場景另外一種LSH的技術更有用。
回顧問題的背景,現在已經預先將圖像庫中的圖像都轉換成了特征并組成特征集合(所有特征的維度都是相同的):
[[20,….,………….61],
…,
[[31,….,………….55]]
同時也用相同的特征提取算法提取了用戶提交圖像的特征,如:
[1,2,3,4,5,6,….,60]
現在的問題是從第一個特征集中找到與用戶圖像特征相似度最高的一些特征。
用一個p穩定分布(p-stable distribution)定義如下:
• 定義:對于一個實數集R上的分布D,如果存在P>=0,對任何n個實數v1,…,vn和n個滿足D分布的變量X1,…,Xn,隨機變量ΣiviXi(向量點乘,一個整數)和(Σi|vi|p)1/pX(p(階)范數,一個整數)有相同的分布,其中X是服從D分布的一個隨機變量,則稱D為 一個p-穩定分布。比如p=1是柯西分布,p=2時是高斯分布。
這里面有幾個基本問題必須要進行背景了解,向量點乘、范數、正態分布、同分布。
向量點乘:2個向量相同維度相乘,再相加。
范數:是具有“長度”概念的函數。向量的0范數,向量中非零元素的個數。向量的1范數,為絕對值之和。向量的2范數,就是通常意義上的模。
正態分布:這個太長見了,不多解釋。
同分布:2個數列同分布,意味著呈線性關系的兩個數列,可以理解為同比例縮放。
用通俗的語言進行解析上述定義就是:
取滿足正態分布的一個數列,與某個特征向量做向量點乘,得到一個數值,這個數值與這個特征向量本身的2階范數(即向量每一維的元素絕對值的平方和再開方,代表向量的長度,也是一個數值),有同分布的性質。
假設有兩個圖像特征X1,X2,用這兩個特征分別與同一個正態分布的數列做向量點乘,所得到的2個數值在一維上的距離與X1,X2在多維上的歐氏距離是同分布的。
設正態分布數值為D,待計算的兩個圖像特征為X1,X2,則有:
|X1.D-X2.D| = (X1 – X2).D 同分布于 (X1 – X2) 的2階范數(即長度)。
(X1 – X2)是向量相減,得到一個新的向量,代表兩個特征的距離向量。
用圖像庫中N個圖像的N個特征分別與同一個正態分布的數列做向量點乘,得到的N個特征在一維上的點,我們用在一維上的點之間的距離度量多維空間的距離,當然這種相近是概率意義下的相近。為了簡化計算,把一維上的線劃分成段;為了提高算法的穩定性,向量點乘后增加一個隨機的噪音。于是得到了一個新的哈希函數:
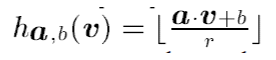
a是p穩定生成的隨機數列
b是(0,r)里的隨機數, noise/隨機噪音
r為直線上分段的段長
V待計算特征向量,即圖像提取出來的特征
像這樣一類hash函數稱之為局部敏感hash函數,下面給出局部敏感hash函數的定義:
將這樣的一族hash函數 H={h:S→U} 稱為是(d1,d2,p1,p2)敏感的,如果對于任意H中的函數h,滿足以下2個條件:
– 如果d(O1,O2)<d1,那么Pr[h(O1)=h(O2)]≥p1
– 如果d(O1,O2)>d2,那么Pr[h(O1)=h(O2)]≤p2
其中,O1,O2∈S,表示兩個具有多維屬性的數據對象,d(O1,O2)為2個對象的相異程度,也就是相似度。
通俗的講就是:
• N個值足夠相似時
– 映射為同一hash值的概率足夠大;
• N個值不足夠相似時
– 映射為同一hash值的概率足夠小
可以用下圖來表示:
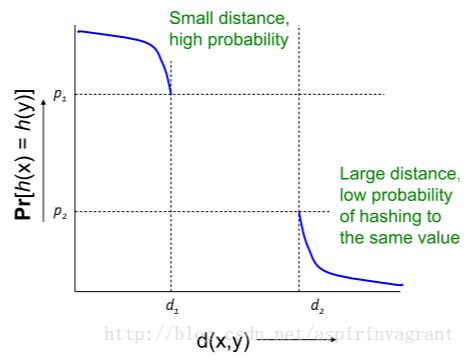
局部敏感HASH函數必要要滿足如下條件:
[1] 進行相似性搜索時,在概率上可以保證返回值的相似性
[2] 函數族中的各函數,返回值在概率上相互獨立,概率獨立可以帶來以下好處
a) 統計獨立,滿足疊加多個函數,提高查準率
b) 通過組合能夠避免偽正例、偽反例
[3] 搜索效率
a) hash比對比線性查詢快
五、概率相似度度量與調節(與構造與或構造)
既然是在概率意義下相似性度量,必然會存在著相近樣本被hash到不同的hash值情況,同時也必然會存在不相近的樣本被hash到相同的hash值情況,前一種稱為偽反例,向一種稱為偽正例。
偽正例通過與構造解決,即通過多個hash函數,計算同一個特征的多個hash值,只有當多個hash函數均相同時,才認為特征相似。這有效避免了不相似的特征被判定為相似特征的情況。
偽反例通過或構造解決,即通過多個hash函數,計算同一個特征的多個hash值,只有多個hash函數有一個hash值相同時,即認為特征相似。這有效避免了相似的特征被判定為不相似特征的情況。
結合與構造與或構造2種方案,可以生成r*b個函數,每r個hash函數帶表一組與構造,每b組hash函數族代表一組或構造,當滿足一個或構造后特征判定為相似。設一組特征hash的相似概率為s,則通過hash函數與/或構造后的相似概率為:
1-(1-s^r)^b
在這個概率函數中,s與hash函數的精度相關,屬于不可調節參數。當r越大時,相似概率越小,當b越大時,相似概率越大。r與b作為LSH的超參數可以根據實際情況進行相應的調節。
六、代碼分析
下面的LIRE上找到一份LSH的代碼實現,這份代碼實現清晰明了,比網上大多數開源出來的代碼要更容易理解。
1 /*
2 * This file is part of the LIRE project: http://www.semanticmetadata.net/lire
3 * LIRE is free software; you can redistribute it and/or modify
4 * it under the terms of the GNU General Public License as published by
5 * the Free Software Foundation; either version 2 of the License, or
6 * (at your option) any later version.
7 *
8 * LIRE is distributed in the hope that it will be useful,
9 * but WITHOUT ANY WARRANTY; without even the implied warranty of
10 * MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
11 * GNU General Public License for more details.
12 *
13 * You should have received a copy of the GNU General Public License
14 * along with LIRE; if not, write to the Free Software
15 * Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA
16 *
17 * We kindly ask you to refer the any or one of the following publications in
18 * any publication mentioning or employing Lire:
19 *
20 * Lux Mathias, Savvas A. Chatzichristofis. Lire: Lucene Image Retrieval 鈥?
21 * An Extensible Java CBIR Library. In proceedings of the 16th ACM International
22 * Conference on Multimedia, pp. 1085-1088, Vancouver, Canada, 2008
23 * URL: http://doi.acm.org/10.1145/1459359.1459577
24 *
25 * Lux Mathias. Content Based Image Retrieval with LIRE. In proceedings of the
26 * 19th ACM International Conference on Multimedia, pp. 735-738, Scottsdale,
27 * Arizona, USA, 2011
28 * URL: http://dl.acm.org/citation.cfm?id=2072432
29 *
30 * Mathias Lux, Oge Marques. Visual Information Retrieval using Java and LIRE
31 * Morgan & Claypool, 2013
32 * URL: http://www.morganclaypool.com/doi/abs/10.2200/S00468ED1V01Y201301ICR025
33 *
34 * Copyright statement:
35 * ====================
36 * (c) 2002-2013 by Mathias Lux (mathias@juggle.at)
37 * http://www.semanticmetadata.net/lire, http://www.lire-project.net
38 *
39 * Updated: 02.06.13 10:27
40 */ 41 42 package net.semanticmetadata.lire.indexing.hashing;
43 44 import java.io.*;
45 import java.util.zip.GZIPInputStream;
46 import java.util.zip.GZIPOutputStream;
47 48 /**
49 * <p>Each feature vector v with dimension d gets k hashes from a hash bundle h(v) = (h^1(v), h^2(v),  , h^k(v)) with
, h^k(v)) with
50 * h^i(v) = (a^i*v + b^i)/w (rounded down), with a^i from R^d and b^i in [0,w) <br/>
51 * If m of the k hashes match, then we assume that the feature vectors belong to similar images. Note that m*k has to be bigger than d!<br/>
52 * If a^i is drawn from a normal (Gaussian) distribution LSH approximates L2. </p>
53 * <p/>
54 * Note that this is just to be used with bounded (normalized) descriptors.
55 *
56 * @author Mathias Lux, mathias@juggle.at
57 * Created: 04.06.12, 13:42
58 */ 59 public class LocalitySensitiveHashing {
60 private static String name = "lshHashFunctions.obj";
61 // 一組正態分布數列,長250,比實際用到的長一些
62 private static int dimensions = 250;
// max d
63 // 50組正態分布數列(供與/或構造共同使用)
64 public static int numFunctionBundles = 50;
// k
65 // 一維線段的長度,公式中的r
66 public static double binLength = 10;
// w
67 68 private static double[][] hashA =
null;
69 70 71 72 // a
73 private static double[] hashB =
null;
// b
74 private static double dilation = 1d;
// defines how "stretched out" the hash values are.
75 76 /**
77 * Writes a new file to disk to be read for hashing with LSH.
78 *
79 * @throws java.io.IOException
80 */ 81 // 產生hash函數,并存儲到磁盤上
82 public static void generateHashFunctions()
throws IOException {
83 File hashFile =
new File(name);
84 System.out.println(hashFile.getAbsolutePath());
85 if (!hashFile.exists()) {
86 ObjectOutputStream oos =
new ObjectOutputStream(
new GZIPOutputStream(
new FileOutputStream(hashFile)));
87 oos.writeInt(dimensions);
88 oos.writeInt(numFunctionBundles);
89 // 產生點乘結果相加的隨機數噪聲
90 for (
int c = 0; c < numFunctionBundles; c++) {
91 oos.writeFloat((
float) (Math.random() * binLength));
92 }
93 // 產生 numFunctionBundles 組正態分布數列,每組dimensions個數字
94 for (
int c = 0; c < numFunctionBundles; c++) {
95 for (
int j = 0; j < dimensions; j++) {
96 oos.writeFloat((
float) (drawNumber() * dilation));
97 }
98 }
99 oos.close();
100 }
else {
101 System.err.println("Hashes could not be written: " + name + " already exists");
102 }
103 }
104 105 // 指定路徑名版本
106 public static void generateHashFunctions(String name)
throws IOException {
107 File hashFile =
new File(name);
108 if (!hashFile.exists()) {
109 ObjectOutputStream oos =
new ObjectOutputStream(
new GZIPOutputStream(
new FileOutputStream(hashFile)));
110 oos.writeInt(dimensions);
111 oos.writeInt(numFunctionBundles);
112 for (
int c = 0; c < numFunctionBundles; c++) {
113 oos.writeFloat((
float) (Math.random() * binLength));
114 }
115 for (
int c = 0; c < numFunctionBundles; c++) {
116 for (
int j = 0; j < dimensions; j++) {
117 oos.writeFloat((
float) (drawNumber() * dilation));
118 }
119 }
120 oos.close();
121 }
else {
122 System.err.println("Hashes could not be written: " + name + " already exists");
123 }
124 }
125 126 /**
127 * Reads a file from disk and sets the hash functions.
128 *
129 * @return
130 * @throws IOException
131 * @see LocalitySensitiveHashing#generateHashFunctions()
132 */133 public static double[][] readHashFunctions()
throws IOException {
134 return readHashFunctions(
new FileInputStream(name));
135 }
136 137 // 讀取存儲在磁盤上LSH hash函數值,計算圖像特征時反復使用同一套LSH函數
138 public static double[][] readHashFunctions(InputStream in)
throws IOException {
139 ObjectInputStream ois =
new ObjectInputStream(
new GZIPInputStream(in));
140 dimensions = ois.readInt();
141 numFunctionBundles = ois.readInt();
142 double[] tmpB =
new double[numFunctionBundles];
143 for (
int k = 0; k < numFunctionBundles; k++) {
144 tmpB[k] = ois.readFloat();
145 }
146 LocalitySensitiveHashing.hashB = tmpB;
147 double[][] hashFunctions =
new double[numFunctionBundles][dimensions];
148 for (
int i = 0; i < hashFunctions.length; i++) {
149 double[] functionBundle = hashFunctions[i];
150 for (
int j = 0; j < functionBundle.length; j++) {
151 functionBundle[j] = ois.readFloat();
152 }
153 }
154 LocalitySensitiveHashing.hashA = hashFunctions;
155 return hashFunctions;
156 }
157 158 /**
159 * Generates the hashes from the given hash bundles.
160 *
161 * @param histogram
162 * @return
163 */164 // 計算一個特征的numFunctionBundles組hash特征
165 public static int[] generateHashes(
double[] histogram) {
166 double product;
167 int[] result =
new int[numFunctionBundles];
168 for (
int k = 0; k < numFunctionBundles; k++) {
169 product = 0;
170 // 1. 向量點乘
171 for (
int i = 0; i < histogram.length; i++) {
172 product += histogram[i] * hashA[k][i];
173 }
174 // 2. 加上隨機噪音,除一維線段長度
175 result[k] = (
int) Math.floor((product + hashB[k]
/*加上隨機噪音*/) / binLength
/*除一維線段長度*/);
176 }
177 return result;
178 }
179 180 181 /**
182 * Returns a random number distributed with standard normal distribution based on the Box-Muller method.
183 *
184 * @return
185 */186 // Box-Muller算法,產生正態分布數
187 private static double drawNumber() {
188 double u, v, s;
189 do {
190 u = Math.random() * 2 - 1;
191 v = Math.random() * 2 - 1;
192 s = u * u + v * v;
193 }
while (s == 0 || s >= 1);
194 return u * Math.sqrt(-2d * Math.log(s) / s);
195 // return Math.sqrt(-2d * Math.log(Math.random())) * Math.cos(2d * Math.PI * Math.random());
196 }
197 198 public static void main(String[] args) {
199 try {
200 generateHashFunctions();
201 }
catch (IOException e) {
202 e.printStackTrace();
203 }
204 }
205 206 207 }
208
七、總結
本文描述了LSH的適用場景、算法原理與算法分析,并配合源代碼幫助讀者理解算法原理,了解算法的實現要點。
程序員長期養成了從代碼反向學習知識的習慣,但是到了人工智能時代這種學習方式受到了很大的挑戰,在一些復雜的數學背景知識面前,先了解背景知識是深入掌握的前提。
參考文獻:
Website:
[1] http://people.csail.mit.edu/indyk/ (LSH原作者)
[2] http://www.mit.edu/~andoni/LSH/ (E2LSH)
Paper:
[1] Approximate nearest neighbor: towards removing the curse of dimensionality
[2] Similarity search in high dimensions via hashing
[3] Locality-sensitive hashing scheme based on p-stable distributions
[4] MultiProbe LSH Efficient Indexing for HighDimensional Similarity Search
[5] Near-Optimal Hashing Algorithms for Approximate Nearest Neighbor in High Dimensions
Tutorial:
[1] Locality-Sensitive Hashing for Finding Nearest Neighbors
[2] Approximate Proximity Problems in High Dimensions via Locality-Sensitive Hashing
[3] Similarity Search in High Dimensions
Book:
[1] Mining of Massive Datasets
[2] Nearest Neighbor Methods in Learning and Vision: Theory and Practice
Cdoe:
[1] http://sourceforge.net/projects/lshkit/?source=directory
[2] http://tarsos.0110.be/releases/TarsosLSH/TarsosLSH-0.5/TarsosLSH-0.5-Readme.html
[3] http://www.cse.ohio-state.edu/~kulis/klsh/klsh.htm
[4] http://code.google.com/p/likelike/
[5] https://github.com/yahoo/Optimal-LSH
[6] OpenCV LSH(分別位于legacy module和flann module中)
posted on 2018-02-24 13:10
胡滿超 閱讀(8910)
評論(0) 編輯 收藏 引用 所屬分類:
算法 、
搜索引擎