《數(shù)據(jù)結(jié)構(gòu)》這門課是計算機(jī)專業(yè)的核心課程,但往往卻讓人頭痛,因為比較抽象,當(dāng)然了,也許你足夠聰明,并不覺得它有多難,但對我而言,是有點難度,后來我仔細(xì)想了想,到底哪里難?我得出這么個結(jié)論:長篇大論,缺乏圖表。現(xiàn)在的人都喜歡看電影,看電視劇,很少人還熱衷于看小說吧,密密麻麻的文字不如一些圖來得直觀。
另外,我們大多數(shù)人是做應(yīng)用的,不是做研究的,所以我們只需要知道2+3=5,而不需要知道a+b=c。所以我就不深入理論,再說自己也沒那個能力。
好,接下去我就用最一般的例子,最通俗易懂的圖,算法和盡量少的文字,描述某作者需要長篇大論方可完成教材。
一、大圈表示法
面試時候如果讓你寫一個算法,要求復(fù)雜度為Ο(n),你明白是什么意思嗎?說起數(shù)據(jù)結(jié)構(gòu),就先提一下這個表示法吧,后面會用到。
“Ο”,其實不是英文的“O”,它是個希臘字母,發(fā)音大概是“歐麥克隆”,所以我們一般說“圈”而不是跟英文的O一樣的發(fā)音。簡單地說,大圈表示法是一種用于表示算法復(fù)雜度數(shù)量級的方法。要精確描述這個表示法,很難,不過我們不需要懂那么精確,只要八九不離十就可以了。下面我列個表,復(fù)雜度從低到高,大家就知道其意義:
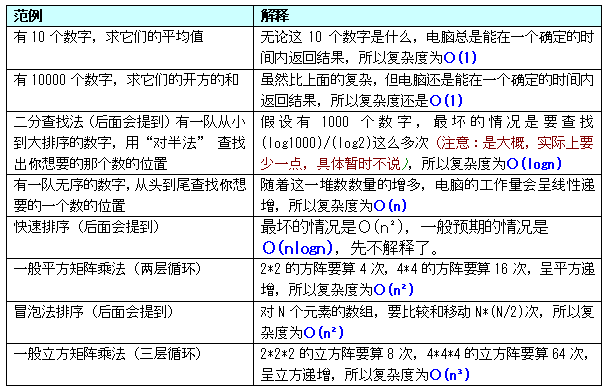
另外還有個叫指數(shù)復(fù)雜度,這里不提,因為見得實在太少,“指數(shù)級遞增”本身就是一個很夸張的形容詞,我們也要避免這種復(fù)雜度的出現(xiàn)。還需要說明的一點是大圈表示法是時間遞增數(shù)量級的表示方法,注意“遞增”兩個字,所以并不是說復(fù)雜度為Ο(1)的算法消耗的時間一定比復(fù)雜度為Ο(n)的算法少。
如果你還是不太明白大圈表示法,不用擔(dān)心,繼續(xù)往下看,會慢慢明白的。
二、動態(tài)數(shù)組(Dynamic Array)
接下去介紹最最基本的兩種數(shù)據(jù)結(jié)構(gòu),即動態(tài)數(shù)組和單向鏈表,其它數(shù)據(jù)結(jié)構(gòu)其實都可以通過這兩者衍生出來。BTW:如果算法太簡單,我就不列出代碼,只稍微描述一下。
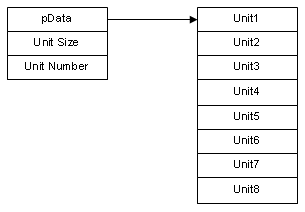
這就是一個最基本的動態(tài)數(shù)組,pData記錄了數(shù)組第一個元素的位置,Unit Size記錄了每個元素的大小,(這樣可以方便地找到第N個元素了)Unit Number記錄了元素的數(shù)目。
獲取數(shù)組中第N個元素,是很簡單的,無需多說。
但已知某位置,要插入一個元素,就稍微有點難,因為要挪動一些元素,如圖:
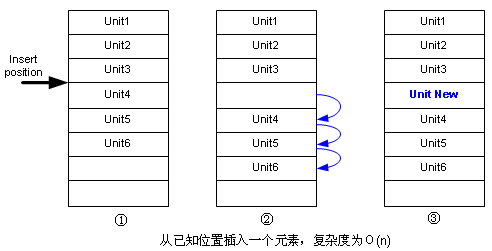
刪除元素跟這個也類似,也是需要挪一挪后面的元素,只不過是往前挪。
數(shù)組的大小不能很方便地調(diào)整,需要幾個步驟,如下圖所示:
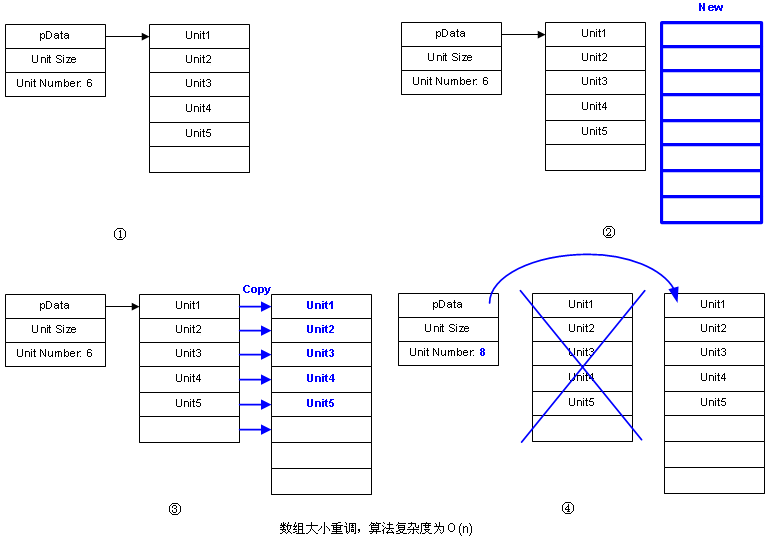
代碼我就不寫了,大概就是new,memcpy,delete這幾個步驟。
三、單向鏈表(Singly-linked List)
下圖就是最簡單最一般的單向鏈表:

還有這種:

多一個Tail指針,好處就是能很方便地找到末尾,然后在末尾插入新的元素什么的。還有這種也比較常見:
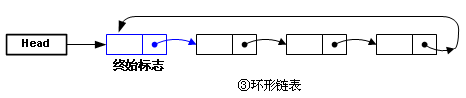
留一個終始標(biāo)志,這個節(jié)點作為一個標(biāo)志,不用于存儲數(shù)據(jù),鏈表末尾指向這個節(jié)點,形成一個“環(huán)形鏈表”,這樣無論在鏈表的哪里插入新的元素,操作都一致了,不必判斷頭和尾的特殊性。
數(shù)組的好處就是鏈表的壞處,數(shù)組的壞處就是鏈表的好處,請看:

因為需要從頭開始找,沒辦法像數(shù)組那樣直接跳到那個地址。而插入元素,就比數(shù)組方便了,如果你已經(jīng)得知了要插入的地址的話,不過還要注意哦,是“后插入”(Insert After):
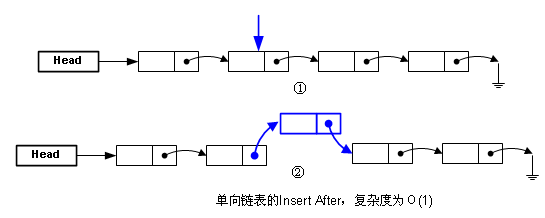
有“后插入”,那就有“前插入”(Insert Before),兩者對單向鏈表來說真的不一樣,下圖描述了“前插入”:
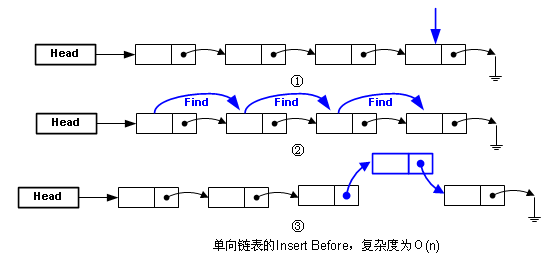
由于指針向后不向前,我們不知道要插入位置的前一個節(jié)點是什么,只能從頭找,所以比較麻煩。
至于鏈表大小的重新調(diào)整,和數(shù)組相比如何呢?呃……我可沒說鏈表有大小限制吧?
(未完待續(xù)……)