国产免费久久精品99久久,久久丫精品国产亚洲av不卡 ,亚洲AV日韩AV天堂久久

圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹

這篇將是最有難度和挑戰(zhàn)性的一篇，做好心理準(zhǔn)備！

十、二叉查找樹（BST）

前一篇介紹了樹，卻未介紹樹有什么用。但就算我不說(shuō)，你也能想得到，看我們Windows的目錄結(jié)構(gòu)，其實(shí)就是樹形的，一個(gè)典型的分類應(yīng)用。當(dāng)然除了分類，樹還有別的作用，我們可以利用樹建立一個(gè)非常便于查找取值又非常便于插入刪除的數(shù)據(jù)結(jié)構(gòu)，這就是馬上要提到的二叉查找樹（Binary Search Tree），這種二叉樹有個(gè)特點(diǎn)：對(duì)任意節(jié)點(diǎn)而言，左子（當(dāng)然了，存在的話）的值總是小于本身，而右子（存在的話）的值總是大于本身。

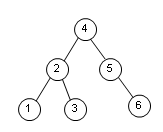
這種特性使得我們要查找其中的某個(gè)值都很容易，從根開(kāi)始，小的往左找，大的往右找，不大不小的就是這個(gè)節(jié)點(diǎn)了；插入一樣的道理，從根開(kāi)始，小的往左，大的往右，直到葉子，就插入，算法比較簡(jiǎn)單，不一一列了，它們的時(shí)間復(fù)雜度期望為Ο(logn)。（為什么是“期望”，后面會(huì)講）

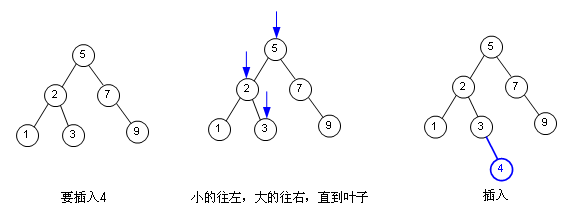
刪除則稍微麻煩點(diǎn)，因?yàn)槲覀儎h的不一定是葉子，如果只是葉子，那就好辦，如果不是呢？我們最通常的做法就是把這個(gè)節(jié)點(diǎn)往下挪，直到它變?yōu)槿~子為止，看圖。

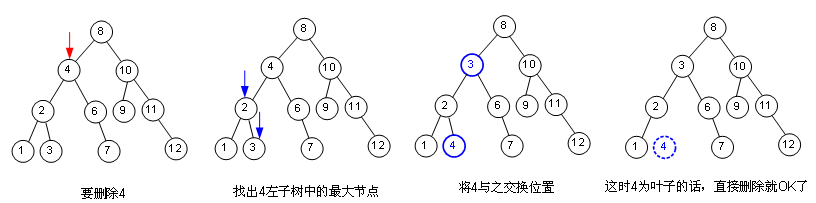
也許你要問(wèn)，如果和左子樹最大節(jié)點(diǎn)交換后，要?jiǎng)h除的節(jié)點(diǎn)依然不是葉子，那怎么辦呢？那繼續(xù)唄，看圖：

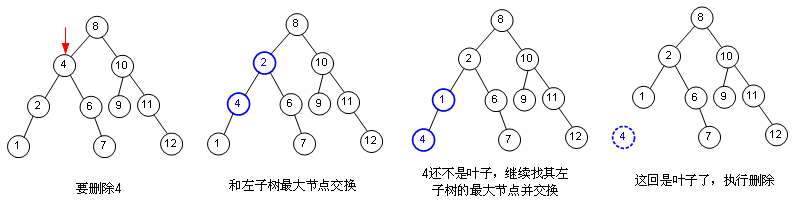
那左子樹不存在的情況下呢？你可以查找右子樹的最小節(jié)點(diǎn)，和上面是類似的，圖我就不畫了。

十一、平衡二叉查找樹（AVL）

前面說(shuō)了，二叉查找樹方便查找取值插入刪除，其復(fù)雜度不過(guò)為Ο(logn)，但這是個(gè)“期望值”，因?yàn)槲覀円灿斜容^差的情況，比如下面這棵樹：

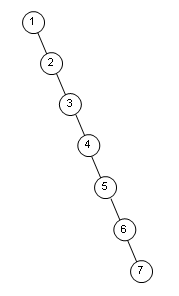
說(shuō)是樹，其實(shí)已經(jīng)退化為鏈表了，但從概念上來(lái)說(shuō)它依然是一棵二叉查找樹，這棵樹怎么形成的呢？很簡(jiǎn)單，我們只要按著1，2，3，4，5，6，7這樣的順序往一個(gè)空的二叉查找樹里添加元素，就形成了。這樣我們?cè)偬砑?，9，10……那真的就變成了一個(gè)鏈表結(jié)構(gòu)，那插入的復(fù)雜度也就變成了Ο(n)。導(dǎo)致這種糟糕的原因是這棵樹非常不平衡，右樹的重量遠(yuǎn)大于左樹，所以我們提出了一種叫“平衡二叉查找樹”的結(jié)構(gòu)，平衡二叉查找樹英文叫AVL，而不是我本來(lái)以為的什么Balance BST，AVL來(lái)自于人名，我這里就不追究了。

平衡，顧名思義，就是兩邊看起來(lái)比較對(duì)稱，但很多時(shí)候我們是做不到絕對(duì)的對(duì)稱（絕對(duì)對(duì)稱即對(duì)任意子樹而言，左右節(jié)點(diǎn)的數(shù)量都相等），因?yàn)橹挥?2^n-1)元素?cái)?shù)目的二叉樹才能做到絕對(duì)對(duì)稱，所以我們使用了“高度”（height）這么個(gè)概念，某節(jié)點(diǎn)的高度指的是它離它的子樹的葉子的最遠(yuǎn)距離：

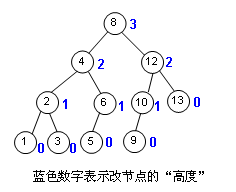
那么我再引申出兩個(gè)概念，左高和右高：
左高 = 左節(jié)點(diǎn)空 ? 0 : (左節(jié)點(diǎn)高+1)
右高 = 右節(jié)點(diǎn)空 ? 0 : (右節(jié)點(diǎn)高+1)

那我們就可以給AVL下個(gè)定義了，對(duì)AVL的任意節(jié)點(diǎn)而言：

ABS(左高 - 右高) <= 1

做到了這點(diǎn)，這棵樹看起來(lái)就比較平衡了，如何生成一棵AVL樹呢？算法十分不簡(jiǎn)單，那我們先通過(guò)圖來(lái)獲得一些最直觀的認(rèn)識(shí)，就先按1，2，3，4……這樣的自然數(shù)順序加入到樹中，下圖體現(xiàn)出了樹的構(gòu)造變化：

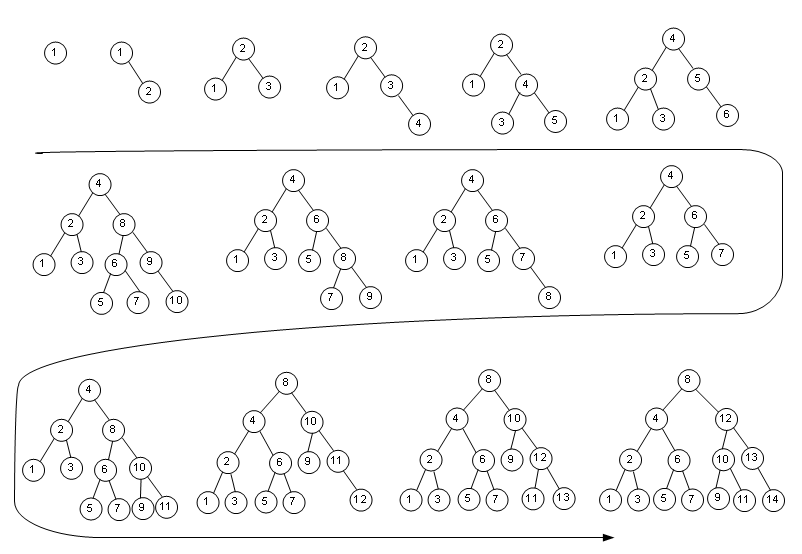
隨著新節(jié)點(diǎn)的加入，樹自動(dòng)調(diào)整自身結(jié)構(gòu)，達(dá)到新的平衡狀態(tài)，這就是我們想要的AVL樹。我們先要分析，為什么樹會(huì)失衡？是由于插入了一個(gè)元素，對(duì)吧，那我們能不能把不同的插入情況全部概括起來(lái)并作出統(tǒng)一的調(diào)整來(lái)使得樹重新平衡？答案是肯定的，也有人幫我們研究好了，只是證明這個(gè)過(guò)程需要一些數(shù)學(xué)功底，我是不行的了，所以直接給出算法示意圖和范例。

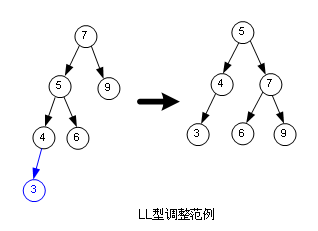
LL型調(diào)整：

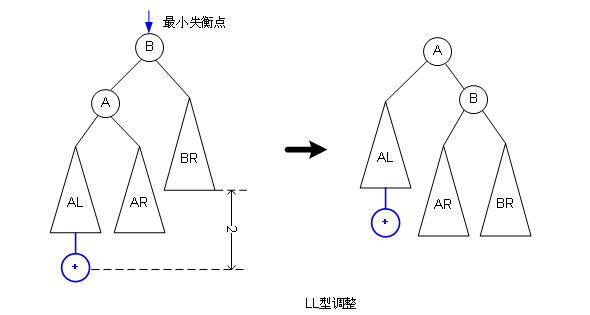
再給一個(gè)LL型調(diào)整的實(shí)例：

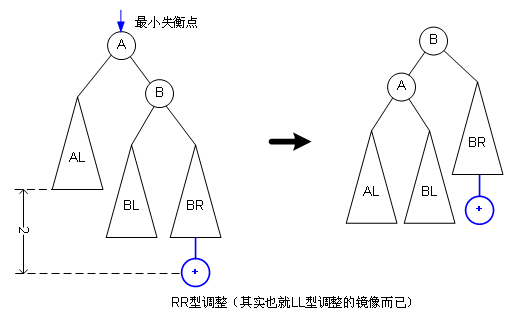
RR型調(diào)整，其實(shí)就是LL型調(diào)整的鏡像而已：

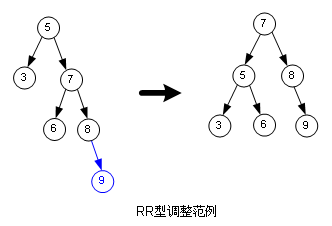
這是一個(gè)RR型調(diào)整的實(shí)例：

接下去就是LR型調(diào)整：

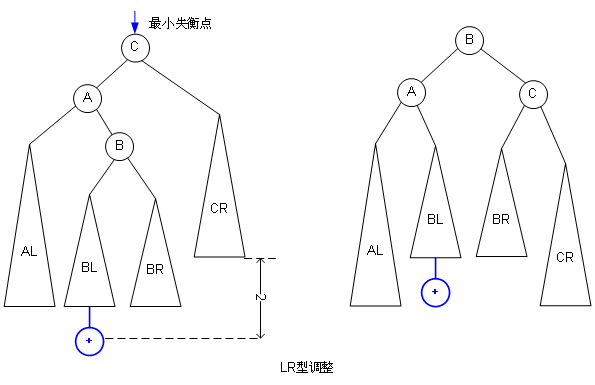
這是一個(gè)LR型調(diào)整的實(shí)例：

RL型調(diào)整是LR型調(diào)整的鏡像，所以不再畫圖了。

至于如何選擇不同的調(diào)整類型，我后面將給出代碼，看“DoBalance”這個(gè)函數(shù)的實(shí)現(xiàn)，很清晰的。那接下去我們還要面臨一個(gè)比較困難的問(wèn)題，就是刪除及刪除平衡，因?yàn)椴还馐遣迦朐乜赡軐?dǎo)致不平衡，刪除也會(huì)。不過(guò)我們都有個(gè)同樣的前提，就是無(wú)論是插入前還是刪除前的二叉樹，都是平衡的。

我參考的書上說(shuō)刪除和插入其實(shí)是很類似的，具體實(shí)現(xiàn)卻沒(méi)說(shuō)，我后來(lái)寫代碼蠻辛苦的，最后發(fā)現(xiàn)確實(shí)差別不大，但在調(diào)整相關(guān)節(jié)點(diǎn)高度的時(shí)候確實(shí)有點(diǎn)細(xì)微上的差別，這個(gè)在我的代碼里也能看得出來(lái)。下面我就給出我的代碼，我已經(jīng)通過(guò)了初步的測(cè)試，不過(guò)也許代碼還有bug，如果發(fā)現(xiàn)了，請(qǐng)留言。

代碼比較長(zhǎng)，其中還利用了之前的堆棧和隊(duì)列結(jié)構(gòu)，可以算是復(fù)習(xí)，如果覺(jué)得代碼晦澀難懂，也可以跳過(guò)，有些怕自己的代碼寫得不夠好……

另附帶一些代碼說(shuō)明：
1，TreeNode目前只帶一個(gè)“數(shù)據(jù)”，就是iData，所以交換節(jié)點(diǎn)位置時(shí)候，為了方便，只需要交換這個(gè)數(shù)據(jù)；
2，代碼中的pMinBST指向的是“最小不平衡樹”，即：從插入或刪除的位置開(kāi)始往上查找出現(xiàn)的第一個(gè)不平衡的節(jié)點(diǎn)；
3，“往上查找”就需要借助一個(gè)Stack結(jié)構(gòu)；
4，AVL樹的析構(gòu)采用了后序遍歷，由于是析構(gòu)，之后不再用到，所以后序遍歷時(shí)候改變了節(jié)點(diǎn)指針的值，后續(xù)遍歷使用了Queue結(jié)構(gòu)；
5，刪除節(jié)點(diǎn)時(shí)候，尋找并交換葉子節(jié)點(diǎn)的操作有些晦澀，往左尋找最大節(jié)點(diǎn)，為什么找到了最大并交換，而它還不是葉子的時(shí)候，我只需要再往左找并交換一次就可以了呢？因?yàn)槲覄h除到時(shí)候有個(gè)前提：這棵樹是平衡的，往右尋找最小節(jié)點(diǎn)的道理跟這個(gè)一樣的；
6，有什么問(wèn)題請(qǐng)留言。

#include "stdio.h"

// TreeNode
//////////////////////////////////////////////////////////////////////////
struct TreeNode
{
    TreeNode(int iVal);
    int UpdateHeight();
    int GetLeftHeight();
    int GetRightHeight();
    int GetDiff(); //Left Height - Right height

    int iData;

    int iHeight;
    TreeNode* pLeft;
    TreeNode* pRight;
};

TreeNode::TreeNode(int iVal)
{
    iData = iVal;
    iHeight = 0;
    pLeft = 0;
    pRight = 0;
}

int TreeNode::UpdateHeight()
{
    int iHeightLeft = GetLeftHeight();
    int iHeightRight = GetRightHeight();
    if(iHeightLeft==0 && iHeightRight==0)
        iHeight = 0;
    else
        iHeight = (iHeightLeft>iHeightRight)?(iHeightLeft):(iHeightRight);
    return iHeight;
}

int TreeNode::GetLeftHeight()
{
    if(pLeft!=0)
        return pLeft->iHeight + 1;
    else
        return 0;
}

int TreeNode::GetRightHeight()
{
    if(pRight!=0)
        return pRight->iHeight + 1;
    else
        return 0;
}

int TreeNode::GetDiff()
{
    int iHeightLeft = 0;
    int iHeightRight = 0;

    if(pLeft!=0)
        iHeightLeft = pLeft->iHeight + 1;
    if(pRight!=0)
        iHeightRight = pRight->iHeight + 1;

    return iHeightLeft - iHeightRight;
}

// Stack
//////////////////////////////////////////////////////////////////////////
class Stack
{
public:
    Stack(int iAmount = 10);
    ~Stack();

    //return 1 means succeeded, 0 means failed.
    int Pop(TreeNode* & val);
    int Push(TreeNode* val);
    int Top(TreeNode* & val);

    //iterator
    int GetTop(TreeNode* &val);
    int GetNext(TreeNode* &val);
private:
    TreeNode** m_pData;
    int m_iCount;
    int m_iAmount;

    //iterator
    int m_iCurr;
};

Stack::Stack(int iAmount)
{
    m_pData = new TreeNode*[iAmount];
    m_iCount = 0;
    m_iAmount = iAmount;
    m_iCurr = 0;
}

Stack::~Stack()
{
    delete m_pData;
}

int Stack::Pop(TreeNode* & val)
{
    if(m_iCount>0)
    {
        --m_iCount;
        val = m_pData[m_iCount];
        return 1;
    }
    return 0;
}

int Stack::Push(TreeNode* val)
{
    if(m_iCount<m_iAmount)
    {
        m_pData[m_iCount] = val;
        ++m_iCount;
        return 1;
    }
    return 0;
}

int Stack::Top(TreeNode* & val)
{
    if(m_iCount>0 && m_iCount<=m_iAmount)
    {
        val = m_pData[m_iCount-1];
        return 1;
    }
    return 0;
}

int Stack::GetTop(TreeNode* &val)
{
    if(m_iCount>0 && m_iCount<=m_iAmount)
    {
        val = m_pData[m_iCount-1];
        m_iCurr = m_iCount - 1;
        return 1;
    }
    return 0;
}

int Stack::GetNext(TreeNode* &val)
{
    if((m_iCurr-1)<(m_iCount-1) && (m_iCurr-1)>=0)
    {
        --m_iCurr;
        val = m_pData[m_iCurr];
        return 1;
    }
    return 0;
}

// The Queue
//////////////////////////////////////////////////////////////////////////
class Queue
{
public:
    Queue(int iAmount=10);
    ~Queue();

    //return 0 means failed, return 1 means succeeded.
    int Enqueue(TreeNode* node);
    int Dequeue(TreeNode* & node);
private:
    int m_iAmount;
    int m_iCount;
    TreeNode** m_ppFixed; //The pointer array to implement the queue.

    int m_iHead;
    int m_iTail;
};

Queue::Queue(int iAmount)
{
    m_iCount = 0;
    m_iAmount = iAmount;
    m_ppFixed = new TreeNode*[iAmount];

    m_iHead = 0;
    m_iTail = iAmount-1;
}

Queue::~Queue()
{
    delete[] m_ppFixed;
}

int Queue::Enqueue(TreeNode* node)
{
    if(m_iCount<m_iAmount)
    {
        ++m_iTail;
        if(m_iTail > m_iAmount-1)
            m_iTail = 0;
        m_ppFixed[m_iTail] = node;
        ++m_iCount;
        return 1;
    }
    else
        return 0;
}

int Queue::Dequeue(TreeNode* & node)
{
    if(m_iCount>0)
    {
        node = m_ppFixed[m_iHead];
        ++m_iHead;
        if(m_iHead > m_iAmount-1)
            m_iHead = 0;
        --m_iCount;
        return 1;
    }
    else
        return 0;
}

// AVLTree
//////////////////////////////////////////////////////////////////////////
class CAVLTree
{
public:
    CAVLTree();
    ~CAVLTree();

    TreeNode* Insert(int iVal);
    int Delete(int iVal);
    TreeNode* FindNode(int iVal); //the find function, returns 0 means not found.

#ifdef _DEBUG
    void PrintTree();
#endif

protected:
    //Update the height after insert or delete.
    //And find the minimum unbalance BST.
    int UpdateHeight(Stack &st, TreeNode* &pMinBST, TreeNode* &pMinBSTParent, int& iLeftRight);

    //Rotate
    void DoBalance(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight);
    void LLRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight);
    void RRRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight);
    void LRRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight, int iSpecialFlag=0);
    void RLRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight, int iSpecialFlag=0);

    void SwapTwoNodes(TreeNode *pNode1, TreeNode *pNode2); //Swap their value only.

    TreeNode *m_pRoot;
};

CAVLTree::CAVLTree()
{
    m_pRoot = NULL;
}

CAVLTree::~CAVLTree()
{
    Stack st(40); //2^40 must be enough.

    //Postorder traverse the tree to release all nodes.
    TreeNode *pNode = m_pRoot;
    TreeNode *pTemp;
    if(pNode==0)
        return;

    while (1)
    {
        if(pNode->pLeft!=0)
        {
            st.Push(pNode);
            pTemp = pNode;
            pNode = pNode->pLeft;
            pTemp->pLeft = 0;
            continue;
        }

        if(pNode->pRight!=0)
        {
            st.Push(pNode);
            pTemp = pNode;
            pNode = pNode->pRight;
            pTemp->pRight = 0;
            continue;
        }

        delete pNode;

        if(0==st.Pop(pNode))
            break;
    }
}

TreeNode* CAVLTree::Insert(int iVal)
{
    Stack st(40); //To record the path.
    TreeNode *pNode = m_pRoot;
    TreeNode *pIns;
    int iLeftOrRight; // 0 means left, 1 means right.
    while (1)
    {
        if(pNode==0) //Insert at this position
        {
            TreeNode *pNew = new TreeNode(iVal);
            TreeNode *pPrev;
            if(0!=st.Top(pPrev))
            {
                if(0==iLeftOrRight)
                    pPrev->pLeft = pNew;
                else
                    pPrev->pRight = pNew;
            }
            else //The root
            {
                m_pRoot = pNew;
                return m_pRoot;
            }

            pIns = pNew;
            if(0==iLeftOrRight && pPrev->pRight!=0 || 1==iLeftOrRight && pPrev->pLeft!=0) //Need not to change.
                return pIns;

            break;
        }

        if(iVal<pNode->iData)
        {
            st.Push(pNode);
            pNode = pNode->pLeft;
            iLeftOrRight = 0;
        }
        else if(iVal>pNode->iData)
        {
            st.Push(pNode);
            pNode = pNode->pRight;
            iLeftOrRight = 1;
        }
        else
            return pNode;
    }

    TreeNode* pMinBST;
    TreeNode* pMinBSTParent;
    int iLRParent;
    UpdateHeight(st, pMinBST, pMinBSTParent, iLRParent);
    if(pMinBST!=0) //It exists. need balance.
    {
        DoBalance(pMinBST, pMinBSTParent, iLRParent);
    }
    return pIns;
}

//Update the height after insert or delete.
int CAVLTree::UpdateHeight(Stack &st, TreeNode* &pMinBST, TreeNode* &pMinBSTParent, int& iLRParent)
{
    TreeNode *pNode;
    pMinBST = 0;
    pMinBSTParent = 0;

    if(0==st.GetTop(pNode))
        return 0;

    while(1)
    {
        pNode->UpdateHeight();
        int iDiff = pNode->GetDiff();
        if(iDiff>1 || iDiff<-1) //unbalance
        {
            pMinBST = pNode;
            if(0!=st.GetNext(pMinBSTParent))
            {
                if(pMinBSTParent->pLeft==pMinBST)
                    iLRParent = 0; //left
                else
                    iLRParent = 1; //right
            }
            return 0;
        }

        if(0==st.GetNext(pNode))
            break;
    }

    return 0;
}

void CAVLTree::DoBalance(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight)
{
    if(pNode->GetLeftHeight() < pNode->GetRightHeight())
    {
        if(pNode->pRight->GetLeftHeight() < pNode->pRight->GetRightHeight())
            RRRotate(pNode, pMinBSTParent, iLeftRight);
        else if(pNode->pRight->GetLeftHeight() > pNode->pRight->GetRightHeight())
            RLRotate(pNode, pMinBSTParent, iLeftRight);
        else
            RLRotate(pNode, pMinBSTParent, iLeftRight, 1);
    }
    else
    {
        if(pNode->pLeft->GetLeftHeight() > pNode->pLeft->GetRightHeight())
            LLRotate(pNode, pMinBSTParent, iLeftRight);
        else if(pNode->pLeft->GetLeftHeight() < pNode->pLeft->GetRightHeight())
            LRRotate(pNode, pMinBSTParent, iLeftRight);
        else
            LRRotate(pNode, pMinBSTParent, iLeftRight, 1);
    }
}

//      B               A
//     / \             / \
//    A   BR    =>    AL  B
//   / \              +  / \
//  AL  AR              AR  BR
//  +
void CAVLTree::LLRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight)
{
    //B, A and AL must be exist. BR and AR may be null.
    TreeNode *pNodeB = pNode;
    TreeNode *pNodeA = pNodeB->pLeft;
    TreeNode *pNodeAR = pNodeA->pRight;
    pNodeA->pRight = pNodeB;
    pNodeB->pLeft = pNodeAR;

    //Handle the height
    pNodeB->iHeight -= 2;

    if(pMinBSTParent==0) //root
        m_pRoot = pNodeA;
    else
    {
        if(iLeftRight==0) //left
            pMinBSTParent->pLeft = pNodeA;
        else
            pMinBSTParent->pRight = pNodeA;
    }
}

//      A                B
//     / \              / \
//    AL  B      =>    A   BR
//       / \          / \  +
//      BL  BR       AL  BL
//          +
void CAVLTree::RRRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight)
{
    TreeNode *pNodeA = pNode;
    TreeNode *pNodeB = pNodeA->pRight;
    TreeNode *pNodeBL = pNodeB->pLeft;
    pNodeB->pLeft = pNodeA;
    pNodeA->pRight = pNodeBL;

    //Handle the height
    pNodeA->iHeight -= 2;

    if(pMinBSTParent==0) //root
        m_pRoot = pNodeB;
    else
    {
        if(iLeftRight==0) //left
            pMinBSTParent->pLeft = pNodeB;
        else
            pMinBSTParent->pRight = pNodeB;
    }
}

//          C                   B
//         / \                /   \
//        A   CR             A     C
//       / \         =>     / \   / \
//      AL  B              AL BL BR CR
//         / \                   +
//        BL  BR
//            +
// Special flag is used for some kind of delete operation, for example:
//        4                   3
//       / \                 / \
//      2   5(-)    =>      2   4
//     / \                 /
//    1   3               1
void CAVLTree::LRRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight, int iSpecialFlag)
{
    TreeNode *pNodeC = pNode;
    TreeNode *pNodeA = pNodeC->pLeft;
    TreeNode *pNodeB = pNodeA->pRight;
    TreeNode *pNodeBL = pNodeB->pLeft;
    TreeNode *pNodeBR = pNodeB->pRight;
    pNodeB->pLeft = pNodeA;
    pNodeB->pRight = pNodeC;
    pNodeA->pRight = pNodeBL;
    pNodeC->pLeft = pNodeBR;

    //Handle the height
    if(iSpecialFlag==0)
    {
        pNodeA->iHeight -= 1;
        pNodeB->iHeight += 1;
    }
    else
    {
        pNodeB->iHeight += 2;
    }
    pNodeC->iHeight -= 2;

    if(pMinBSTParent==0) //root
        m_pRoot = pNodeB;
    else
    {
        if(iLeftRight==0) //left
            pMinBSTParent->pLeft = pNodeB;
        else
            pMinBSTParent->pRight = pNodeB;
    }
}

//          B                   A
//         / \                /   \
//        BL  C              B     C
//           / \      =>    / \   / \
//          A   CR         BL AL AR CR
//         / \                   +
//        AL  AR
//            +
// Special flag is used for some kind of delete operation, for example:
//        3                   4
//       / \                 / \
//   (-)2   5      =>       3   5
//         / \                   \
//        4   6                   6
void CAVLTree::RLRotate(TreeNode *pNode, TreeNode* pMinBSTParent, int iLeftRight, int iSpecialFlag)
{
    TreeNode *pNodeB = pNode;
    TreeNode *pNodeC = pNodeB->pRight;
    TreeNode *pNodeA = pNodeC->pLeft;
    TreeNode *pNodeAL = pNodeA->pLeft;
    TreeNode *pNodeAR = pNodeA->pRight;
    pNodeA->pLeft = pNodeB;
    pNodeA->pRight = pNodeC;
    pNodeC->pLeft = pNodeAR;
    pNodeB->pRight = pNodeAL;

    //Handle the height
    if(iSpecialFlag==0)
    {
        pNodeC->iHeight -= 1;
        pNodeA->iHeight += 1;
    }
    else
    {
        pNodeA->iHeight += 2;
    }
    pNodeB->iHeight -= 2;

    if(pMinBSTParent==0) //root
        m_pRoot = pNodeA;
    else
    {
        if(iLeftRight==0) //left
            pMinBSTParent->pLeft = pNodeA;
        else
            pMinBSTParent->pRight = pNodeA;
    }
}

int CAVLTree::Delete(int iVal)
{
    if(m_pRoot==0)
        return 0;

    Stack st(40); //To record the path.
    TreeNode *pNode = m_pRoot;
    TreeNode *pPrev;
    int iLeftOrRight; // 0 means left, 1 means right.

    while (1)
    {
        if(pNode->iData==iVal) //Yes, it is.
        {
            st.Push(pNode);
            break;
        }

        if(iVal<pNode->iData)
        {
            st.Push(pNode);
            if(pNode->pLeft!=0)
                pNode = pNode->pLeft;
            else
                return 0;
            iLeftOrRight = 0;
        }
        else //iVal > pNode->iData
        {
            st.Push(pNode);
            if(pNode->pRight!=0)
                pNode = pNode->pRight;
            else
                return 0;
            iLeftOrRight = 1;
        }
    }

    int iLeafLeftRight;

    if(pNode->iHeight==0) //It is the leaf node.
    {
        if(0!=st.GetTop(pPrev))
        {
            iLeafLeftRight = iLeftOrRight;
        }
        else //The root, this tree is going to be null.
        {
            delete m_pRoot;
            m_pRoot = 0;
            return 0;
        }
    }
    else if(pNode->pLeft!=NULL)
    {
        iLeafLeftRight = 0;
        //Move this node to the bottom.
        TreeNode *pBiggestLeft = pNode->pLeft;
        st.Push(pBiggestLeft);
        while(pBiggestLeft->pRight!=NULL)
        {
            pBiggestLeft = pBiggestLeft->pRight;
            st.Push(pBiggestLeft);
            iLeafLeftRight = 1;
        }
        SwapTwoNodes(pBiggestLeft, pNode);
        if(pBiggestLeft->pLeft!=NULL)
        {
            SwapTwoNodes(pBiggestLeft, pBiggestLeft->pLeft);
            st.Push(pBiggestLeft->pLeft);
            iLeafLeftRight = 0;
        }
    }
    else //pNode->pRight!=NULL
    {
        iLeafLeftRight = 1;
        //Move this node to the bottom.
        TreeNode *pLeastRight = pNode->pRight;
        st.Push(pLeastRight);
        while(pLeastRight->pLeft!=NULL)
        {
            pLeastRight = pLeastRight->pLeft;
            st.Push(pLeastRight);
            iLeafLeftRight = 0;
        }
        SwapTwoNodes(pLeastRight, pNode);
        if(pLeastRight->pRight!=NULL)
        {
            SwapTwoNodes(pLeastRight, pLeastRight->pRight);
            st.Push(pLeastRight->pRight);
            iLeafLeftRight = 1;
        }
    }

    //Delete the leaf.
    TreeNode *pToDel;
    st.Pop(pToDel);
    delete pToDel;
    TreeNode *pToChange;
    st.GetTop(pToChange);
    if(iLeafLeftRight==0)
        pToChange->pLeft = 0;
    else
        pToChange->pRight = 0;

    TreeNode* pMinBST;
    TreeNode* pMinBSTParent;
    int iLRParent;
    UpdateHeight(st, pMinBST, pMinBSTParent, iLRParent);
    if(pMinBST!=0) //It exists. need balance.
    {
        DoBalance(pMinBST, pMinBSTParent, iLRParent);
    }

    return 0;
}

TreeNode* CAVLTree::FindNode(int iVal)
{
    TreeNode* pNode = m_pRoot;
    while (pNode!=0)
    {
        if(iVal<pNode->iData)
            pNode = pNode->pLeft;
        else if(iVal>pNode->iData)
            pNode = pNode->pRight;
        else
            return pNode;
    }

    return 0;
}

void CAVLTree::SwapTwoNodes(TreeNode *pNode1, TreeNode *pNode2)
{
    int iDataTmp = pNode1->iData;

    pNode1->iData = pNode2->iData;

    pNode2->iData = iDataTmp;
}

#ifdef _DEBUG

void CAVLTree::PrintTree()
{
    printf("--------------------\n");
    if(m_pRoot==0)
    {
        printf("null tree.\n");
        return;
    }
    Queue que(100);
    que.Enqueue(m_pRoot);
    TreeNode* pNode;
    while (0!=que.Dequeue(pNode))
    {
        if(pNode->pLeft!=0 && pNode->pRight!=0)
        {
            printf("%d(%d) -> %d %d\n", pNode->iData, pNode->iHeight, pNode->pLeft->iData, pNode->pRight->iData);
            que.Enqueue(pNode->pLeft);
            que.Enqueue(pNode->pRight);
        }
        else if(pNode->pLeft!=0)
        {
            que.Enqueue(pNode->pLeft);
            printf("%d(%d) -> %d x\n", pNode->iData, pNode->iHeight, pNode->pLeft->iData);
        }
        else if(pNode->pRight!=0)
        {
            que.Enqueue(pNode->pRight);
            printf("%d(%d) -> x %d\n", pNode->iData, pNode->iHeight, pNode->pRight->iData);
        }
    }
}

#endif

// Main
//////////////////////////////////////////////////////////////////////////
int main(int argc, char* argv[])
{
    CAVLTree avl;
    avl.Insert(14);
    avl.Insert(11);
    avl.Insert(13);
    avl.Insert(1);
    avl.Insert(4);
    avl.Insert(3);
    avl.Insert(15);
    avl.Insert(2);
    avl.Insert(9);
    avl.Insert(10);
    avl.Insert(8);
    avl.Insert(7);

    avl.Delete(10);
    avl.Delete(8);
    avl.Delete(7);
    avl.Delete(13);
#ifdef _DEBUG
    avl.PrintTree();
#endif

    return 0;
}

代碼中有些注釋顯示得不太正常，這是因?yàn)檫@個(gè)博客中的代碼部分不適用等寬字符的緣故，拿到你的IDE下看就正常了。

posted on 2009-10-26 17:18 Jiang Guogang 閱讀(6671) 評(píng)論(8) 編輯收藏引用所屬分類: Knowledge

評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹 2009-10-26 17:46 matthew0816

國(guó)綱，我的基礎(chǔ)知識(shí)只能靠你來(lái)補(bǔ)了回復(fù) 更多評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹 2009-10-26 17:46 matthew0816

繼續(xù)努力呢，
這個(gè)系列很棒，
完全可以開(kāi)課了回復(fù) 更多評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹[未登錄](méi) 2009-12-29 21:08 hao

LZ，你的數(shù)據(jù)結(jié)構(gòu)系列的課程真是講得太好了！！！！
用力地頂啊！！！！

如果再講一下B+樹和B-樹那就更好了，呵呵。回復(fù) 更多評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹 2010-08-20 07:43 自學(xué)數(shù)據(jù)結(jié)構(gòu)者

LZ能講其他的嗎,希望繼續(xù)哦回復(fù) 更多評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹 2010-08-20 15:26 Jiang Guogang

我是樓主，謝謝捧場(chǎng)，其實(shí)我對(duì)數(shù)據(jù)結(jié)構(gòu)了解也不多，寫這幾篇文章時(shí)候正好空余時(shí)間比較多，我也是花了不少時(shí)間整理的。目前寫不出這種文章了。回復(fù) 更多評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹 2011-06-19 00:54 龍?bào)J樓

樓主寫得太棒了，一圖勝千言啊，代碼也不錯(cuò)，傳世經(jīng)典啊回復(fù) 更多評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹 2011-12-11 00:09 thunder

有木有構(gòu)建最佳二叉排序樹的吖？回復(fù) 更多評(píng)論

# re: 圖解數(shù)據(jù)結(jié)構(gòu)（7）——二叉查找樹及平衡二叉查找樹 2016-04-28 08:28 666

66666 回復(fù) 更多評(píng)論

刷新評(píng)論列表

只有注冊(cè)用戶登錄后才能發(fā)表評(píng)論。
【推薦】100%開(kāi)源！大型工業(yè)跨平臺(tái)軟件C++源碼提供，建模，組態(tài)！

相關(guān)文章: 用VS2010發(fā)布ASP.net網(wǎng)站 C#實(shí)現(xiàn)類似C++功能的困惑讓wprintf正常打印漢字根據(jù)下標(biāo)數(shù)組重調(diào)位置發(fā)現(xiàn)MSDN離線文檔的第一個(gè)錯(cuò)別字保存QQ空間的網(wǎng)頁(yè)至本地一個(gè)"滾動(dòng)數(shù)組"類模板怪異的有符號(hào)/無(wú)符號(hào)轉(zhuǎn)換問(wèn)題 VSS使用手記一些可能你不知道的printf的參數(shù)

網(wǎng)站導(dǎo)航: 博客園 IT新聞 BlogJava 博問(wèn) Chat2DB 管理

Jiang's C++ Space

公告

留言簿(16)

隨筆分類

隨筆檔案

最新隨筆

最新評(píng)論

評(píng)論