思路：
先畫一棵完全二叉樹， 為節省空間，采用數組來實現。對這棵二叉樹，葉子用于存放數據，節點用于統計葉子信息。
通過下面的三種方法，進一步節省空間：
1 節點只記錄左子樹葉子信息，右子樹葉子信息通過當前節點和父節點等節點的值計算得出。
因而需要指定一個點，當作根節點的“父節點”，以便計算根節點右子樹信息。
可以將根節點從1開始編號，對節點i，左孩子編號為2*i，右孩子編號為2*i+1，并用編號0記錄整根樹所有葉子的信息。
2 對某些應用，葉子信息可以通過節點信息計算得出，因而不保存葉子信息，
3 完全二叉樹，邊界要求為2^k，為了表示[0, n)這n個點，需要將n增加到2^k，實際上，
只要第n個葉子的父節點r存在就可以了，編號大于r的節點根本不會被訪問到，因而沒必要分配空間
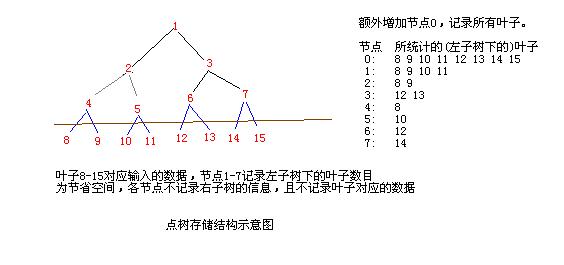
點樹的實現
// www.cnblogs.com/flyinghearts
#include<cstdio>
#include<cstdlib>
#include<cstring>
template<int N> struct Round2k 
{
enum { down = Round2k<N / 2u>::down * 2,
up = down == N ? down : 2 * down };
};
template<> struct Round2k<1> {
enum { down = 1, up = 1};
};
//若表示的區間為[0, M), 則 N >= (M+1+Extra)/2, 其中Extra為大等于m的最小2^t
//完全二叉樹,根節點為1，對節點i，左孩子為2*i，右孩子為2*i+1
//節點編號范圍[1, Extra) 葉子編號范圍[Extra, 2*Extra)， 點n 對應 葉子n+Extra，
//為節省空間，只記錄各節點左子樹下的葉子的個數，不記錄葉子出現的個數
//info[0] 保存所有葉子的總個數， info[i]記錄節點i的左子樹下的所有葉子的總個數）
template <int M, typename T = int> //區間[0, M)
class PointTree {
enum { Extra = Round2k<M>::up, N = (M + 1 + Extra) / 2u };
// T data[M];
T info[N];
public:
PointTree() { clear(); }
void clear() { memset(this, 0, sizeof(*this));}
int size() { return info[0]; }
int capacity() { return N; }
void add(int n) {
++info[0];
for (int i = Extra + n; i > 1; i /= 2u)
if (i % 2u == 0) ++info[i / 2u];
}
void erease(int n) {
--info[0];
for (int i = Extra + n; i > 1; i /= 2u)
if (i % 2u == 0) --info[i / 2u];
}
void erease_safe(int n) { if (count(n)) return erease(n); }
int count(int n) {
// int sum = 0, i = Extra + n;
// while (i % 2u) sum += info[(i /= 2u)];
// return info[i / 2u] - sum;
int i = Extra + n;
if (i % 2u == 0) return info[i / 2u];
int sum = 0;
do { i /= 2u; sum += info[i]; } while (i % 2u);
return info[i / 2u] - sum;
}
int lt(int n) {
int sum = 0 ;
for (int i = Extra + n; i > 1; i /= 2u )
if (i % 2u) sum += info[i / 2u];
return sum;
}
int lteq(int n) {
//if (n == N - 1) return info[0];
if (N == Extra && n == N - 1) return info[0];
return lt(n + 1);
}
int gt(int n) { return info[0] - lteq(n); }
int gteq(int n) { return info[0] - lt(n); }
int operator[](int n) { //第n+1小
int i = 1;
while (i < Extra) {
if (n < info[i]) { i *= 2; }
else { n -= info[i]; i = i * 2 + 1; }
}
return i - Extra;
}
};
int ra(int arr[], int len) //求逆序數
{
int sum = 0;
for (int i = 0; i < len - 1; ++i)
for (int j = i + 1; j < len; ++j)
if (arr[i] > arr[j]) ++sum;
return sum;
}
template<int N>
int rb(int arr[], int len) //求逆序數 點樹實現
{
PointTree<N> pt;
int sum = 0;
for (int i = 0; i < len; ++i) {
pt.add(arr[i]);
sum += pt.gt(arr[i]);
}
return sum;
}
int main()
{
const int N = 6;
int arr[N] = { 4, 3,2,1,0,5};
printf("%d \n", ra(arr, N));
printf("%d \n", rb<N>(arr, N));
}
作者： flyinghearts
出處： http://www.cnblogs.com/flyinghearts/
本文采用知識共享署名-非商業性使用-相同方式共享 2.5 中國大陸許可協議進行許可，歡迎轉載，但未經作者同意必須保留此段聲明，且在文章頁面明顯位置給出原文連接，否則保留追究法律責任的權利。