灰度級(jí)為[0, L-1]范圍內(nèi)的數(shù)字圖像的直方圖是一個(gè)離散函數(shù)h(rk) = nk��,rk是第k級(jí)灰度��,nk是灰度級(jí)為rk的像素個(gè)數(shù)(k = 0, 1, ..., L-1)��。
歸一化的直方圖:P(rk) = nk / n�����,n為圖像中像素點(diǎn)的總數(shù)。
簡(jiǎn)單的說�����,P(rk)給出了灰度級(jí)為rk的發(fā)生的概率估計(jì)值���,提供圖像統(tǒng)計(jì)資料���。歸一化的直方圖的所有部分之和應(yīng)為1�����。
直方圖是多種空間域處理技術(shù)的基礎(chǔ)�����,直方圖能有效的利用于圖像增強(qiáng),壓縮與分割。
若一幅圖像像素占有全部可能的灰度級(jí),并且分部均勻��,這樣的圖像具有高對(duì)比級(jí)和多變的灰度色調(diào)���。
可以快速的開發(fā)出一種函數(shù)��,該函數(shù)僅僅依靠輸入圖像的直方圖信息��,實(shí)現(xiàn)灰度級(jí)豐富且動(dòng)態(tài)范圍大的圖像。
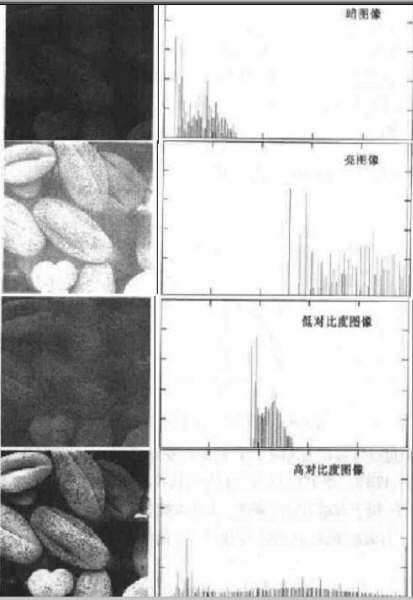
以下圖像是在直方圖在圖像增強(qiáng)中的介紹,四個(gè)基本灰度級(jí)特征(暗���,亮,低對(duì)比度,高對(duì)比度)做出的花粉圖像���。
暗色圖像中,直方圖的組成成分集中在灰度級(jí)低的一側(cè),亮的直方圖傾向于灰度級(jí)高的一側(cè),低對(duì)比度的直方圖集中于灰度級(jí)的中部,
高對(duì)比度的直方圖覆蓋了灰度級(jí)很寬的范圍���,且像素的分部沒有太不均勻,只有少量的曲線比其他的高許多。