Maths - Angle between vectors

LINK: http://www.euclideanspace.com/maths/algebra/vectors/angleBetween/index.htm

How do we calculate the angle between two vectors?

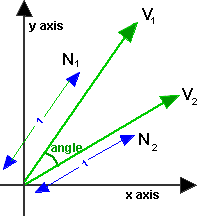
For 2D Vectors

This is relatively simple because there is only one degree of freedom for 2D rotations. If v1 and v2 are normalised so that |v1|=|v2|=1, then,

angle = acos(v1•v2)

where:

• = 'dot' product (see box on right of page).
acos = arc cos = inverse of cosine function see trigonometry page.
|v1|= magnitude of v1.

The only problem is, this won't give all possible values between 0° and 360°, or -180° and +180°. In other words, it won't tell us if v1 is ahead or behind v2, to go from v1 to v2 is the opposite direction from v2 to v1.

In most math libraries acos will usually return a value between 0 and PI (in radians) which is 0° and 180°.

If we want a + or - value to indicate which vector is ahead, then we probably need to use the atan2 function (as explained on this page). using:

angle of 2 relative to 1= atan2(v2.y,v2.x) - atan2(v1.y,v1.x)

For 3D Vectors

Axis Angle Result

This is easiest to calculate using axis-angle representation because:

the angle is given by acos of the dot product of the two (normalised) vectors: v1•v2 = |v1||v2| cos(angle)
the axis is given by the cross product of the two vectors, the length of this axis is given by |v1 x v2| = |v1||v2| sin(angle).

as explained here

this is taken from this discussion.

So, if v1 and v2 are normalised so that |v1|=|v2|=1, then,

angle = acos(v1•v2)

axis = norm(v1 x v2)

If the vectors are parallel (angle = 0 or 180 degrees) then the length of v1 x v2 will be zero because sin(0)=sin(180)=0. In the zero case the axis does not matter and can be anything because there is no rotation round it. In the 180 degree case the axis can be anything at 90 degrees to the vectors so there is a whole range of possible axies.

angle (degrees)	sin(angle)	cos(angle)	v1•v2	v1 x v2
0	0	1	1	0,0,0
90	1	0	0	unit len
180	0	-1	-1	0,0,0
270	-1	0	0	unit len

Quaternion Result

One approach might be to define a quaternion which, when multiplied by a vector, rotates it:

p₂=q * p₁

This almost works as explained on this page.

However, to rotate a vector, we must use this formula:

p₂=q * p₁ * conj(q)

where:

p₂ = is a vector representing a point after being rotated
q = is a quaternion representing a rotation.
p₁= is a vector representing a point before being rotated

This is a bit messy to solve for q, I am therefore grateful to minorlogic for the following approach which converts the axis angle result to a quaternion:

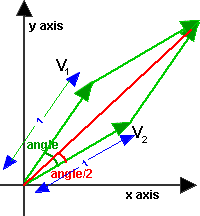
The axis angle can be converted to a quaternion as follows, let x,y,z,w be elements of quaternion, these can be expressed in terms of axis angle as explained here.

angle = arcos(v1•v2/ |v1||v2|)
axis = norm(v1 x v2)
s = sin(angle/2)
x = axis.x *s
y = axis.y *s
z = axis.z *s
w = cos(angle/2)

We can use this half angle trig formula on this page: sin(angle/2) = 0.5 sin(angle) / cos(angle/2)

so substituting in quaternion formula gives:
s = 0.5 sin(angle) / cos(angle/2)
x = norm(v1 x v2).x *s
y = norm(v1 x v2).y *s
z = norm(v1 x v2).z *s
w = cos(angle/2)

multiply x,y,z and w by 2* cos(angle/2) (this will de normalise the quaternion but we can always normalise later)

x = norm(v1 x v2).x * sin(angle)
y = norm(v1 x v2).y * sin(angle)
z = norm(v1 x v2).z * sin(angle)
w = 2 * cos(angle/2) * cos(angle/2)

now substitute half angle trig formula on this page: cos(angle/2) = sqrt(0.5*(1 + cos (angle)))

x = norm(v1 x v2).x * sin(angle)
y = norm(v1 x v2).y * sin(angle)
z = norm(v1 x v2).z * sin(angle)
w = 1 + cos (angle)

because |v1 x v2| = |v1||v2| sin(angle) we can normalise (v1 x v2) by dividing it with sin(angle),

also apply v1•v2 = |v1||v2| cos(angle)so,

x = (v1 x v2).x / |v1||v2|
y = (v1 x v2).y/ |v1||v2|
z = (v1 x v2).z/ |v1||v2|
w = 1 + v1•v2 / |v1||v2|

If v1 and v2 are already normalised then |v1||v2|=1 so,

x = (v1 x v2).x
y = (v1 x v2).y
z = (v1 x v2).z
w = 1 + v1•v2

If v1 and v2 are not already normalised then multiply by |v1||v2| gives:

x = (v1 x v2).x
y = (v1 x v2).y
z = (v1 x v2).z
w = |v1||v2| + v1•v2

Matrix Result

Using the quaternion to matrix conversion here we get:

1 - 2qy² - 2qz²	2qxqy - 2qzqw	2qxqz + 2qyqw
2qxqy + 2qzqw	1 - 2qx² - 2qz²	2qyqz - 2qxqw
2qxqz - 2qyqw	2qyqz + 2qxqw	1 - 2qx² - 2qy²

so substituting the quaternion results above into the matrix we get:

1 - 2(v1 x v2).y² - 2(v1 x v2).z²	2(v1 x v2).x(v1 x v2).y - 2(v1 x v2).z(1 + v1•v2)	2(v1 x v2).x(v1 x v2).z + 2(v1 x v2).y(1 + v1•v2)
2(v1 x v2).x(v1 x v2).y + 2(v1 x v2).z(1 + v1•v2)	1 - 2(v1 x v2).x² - 2(v1 x v2).z²	2(v1 x v2).y(v1 x v2).z - 2(v1 x v2).x(1 + v1•v2)
2(v1 x v2).x(v1 x v2).z - 2(v1 x v2).y(1 + v1•v2)	2(v1 x v2).y(v1 x v2).z + 2(v1 x v2).x(1 + v1•v2)	1 - 2(v1 x v2).x² - 2(v1 x v2).y²

Substituting the following expansions:

(v1 x v2).x = v1.y * v2.z - v2.y * v1.z
(v1 x v2).y = v1.z * v2.x - v2.z * v1.x
(v1 x v2).z = v1.x * v2.y - v2.x * v1.y
(v1 x v2).x² = v1.y * v2.z * v1.y * v2.z + v2.y * v1.z * v2.y * v1.z - 2 * v2.y * v1.z * v1.y * v2.z
(v1 x v2).y² = v1.z * v2.x * v1.z * v2.x + v2.z * v1.x * v2.z * v1.x - 2* v2.z * v1.x * v1.z * v2.x
(v1 x v2).z² = v1.x * v2.y * v1.x * v2.y +v2.x * v1.y * v2.x * v1.y - 2 * v2.x * v1.y * v1.x * v2.y
v1•v2 = v1.x * v2.x + v1.y * v2.y + v1.z * v2.z

This is getting far too complicated ! can anyone help me simplify this?

Thank you again to minorlogic who gave me the following solution:

Hi !
and i think can help in matrix version.

you can use :
http://www.euclideanspace.com/maths/geometry/rotations/conversions/angleToMatrix/index.htm

And will get some thing :

matrix33 RotAngonst vector3& from, const vector3& to )
{
from.norm();
to.norm();

vector3 vs = cross(from, to); // axis multiplied by sin

vector3 v(vs);
v.norm(); // axis of rotation
float ca = dot(from, to) ; // cos angle

vector3 vt(v*(1.0f - ca));

matrix33 rotM;
rotM.M11 = vt.x * v.x + ca;
rotM.M22 = vt.y * v.y + ca;
rotM.M33 = vt.z * v.z + ca;

vt.x *= v.y;
vt.z *= v.x;
vt.y *= v.z;

rotM.M12 = vt.x - vs.z;
rotM.M13 = vt.z + vs.y;
rotM.M21 = vt.x + vs.z;
rotM.M23 = vt.y - vs.x;
rotM.M31 = vt.z - vs.y;
rotM.M32 = vt.y + vs.x;
return rotM;
}

Code

axis-angle version

sfrotation angleBetween(sfvec3f v1,sfvec3f v2) {
float angle;
// turn vectors into unit vectors
n1 = v1.norm();
n2 = v2.norm();
angle = Math.acos( sfvec3f.dot(n1,n2) );
// if no noticable rotation is available return zero rotation
// this way we avoid Cross product artifacts
if( Math.abs(angle) < 0.0001 ) return new sfrotation( 0, 0, 1, 0 );
// in this case there are 2 lines on the same axis
if(Math.abs(angle)-Math.pi) < 0.001){
n1 = n1.Rotx( 0.5f );
// there are an infinite number of normals
// in this case. Anyone of these normals will be
// a valid rotation (180 degrees). so I rotate the curr axis by 0.5 radians this way we get one of these normals
}
sfvec3f axis = n1;
axis.cross(n2);
return new sfrotation(axis.x,axis.y,axis.z,angle);
}

quaternion version

/** note v1 and v2 dont have to be nomalised, thanks to minorlogic for telling me about this:
* http://www.euclideanspace.com/maths/algebra/vectors/angleBetween/minorlogic.htm
*/
sfquat angleBetween(sfvec3f v1,sfvec3f v2) {
float d = sfvec3f.dot(v1,v2);
sfvec3f axis = v1;
axis.cross(v2);
float qw = (float)Math.sqrt(v1.len_squared()*v2.len_squared()) + d;
if (qw < 0.0001) { // vectors are 180 degrees apart
return (new sfquat(0,-v1.z,v1.y,v1.x)).norm;
}
sfquat q= new sfquat(qw,axis.x,axis.y,axis.z);
return q.norm();
}

matrix version

sfmatrix angleBetween(sfvec3f v1,sfvec3f v2) {
// turn vectors into unit vectors
n1 = v1.norm();
n2 = v2.norm(); 	sfvec3f vs = new sfvec3f(n1);
vs.cross(n2); // axis multiplied by sin	sfvec3f v = new sfvec3f(vs);
v = v.norm(); // axis of rotation
float ca = dot(n1, n2) ; // cos angle	sfvec3f vt = new sfvec3f(v);	vt.scale((1.0f - ca);	sfmatrix rotM = new sfmatrix();
rotM.m11 = vt.x * v.x + ca;
rotM.m22 = vt.y * v.y + ca;
rotM.m33 = vt.z * v.z + ca;	vt.x *= v.y;
vt.z *= v.x;
vt.y *= v.z;	rotM.m12 = vt.x - vs.z;
rotM.m13 = vt.z + vs.y;
rotM.m21 = vt.x + vs.z;
rotM.m23 = vt.y - vs.x;
rotM.m31 = vt.z - vs.y;
rotM.m32 = vt.y + vs.x;
return rotM;
}

Vector Dot Product

The dot product operation multiplies two vectors to give a scalar number (not a vector).

It is defined as follows:

Ax * Bx + Ay * By + Az * Bz

dot product

This page explains this.

Vector Cross Product

cross product

The vector cross product gives a vector (or more strictly - a bivector) which is perpendicular to both the vectors being multiplied. The resulting vector A × B is defined by:

x = Ay * Bz - By * Az
y = Az * Bx - Bz * Ax
z = Ax * By - Bx * Ay

where x,y and z are the components of A × B

This page explains this.

Standards

There are a lot of choices we need to make in mathematics, for example,

Left or right handed coordinate systems.
Vector shown as row or column.
Matrix order.
Direction of x,y and z coordinates.
Euler angle order
Direction of positive angles
Choice of basis for bivectors
Etc. etc.

A lot of these choices are arbitrary as long as we are consistent about it, different authors tend to make different choices and this leads to a lot of confusion. Where standards exist I have tried to follow them (for example x3d and MathML) otherwise I have at least tried to be consistent across the site. I have documented the choices I have made on this page.

Transforms

rotate

A transform maps every point in a vector space to a possibly different point.

square

When transforming a computer model we transform all the vertices.

To model this using mathematics we can use matrices, quaternions or other algebras which can represent multidimensional linear equations.

This page explains this.

Beginning Game Writing

Here are some pages on this site which aim to help start writing games:

What computer language should I use?
Games tutorials
Rotation in 3 dimensions
Writing a car racing game
Writing a snooker game

posted on 2009-05-31 13:50 zmj 閱讀(1577) 評論(0) 編輯收藏引用

只有注冊用戶登錄后才能發表評論。
【推薦】100%開源！大型工業跨平臺軟件C++源碼提供，建模，組態！



網站導航: 博客園 IT新聞 BlogJava 博問 Chat2DB 管理

1 - 2qy² - 2qz²	2qxqy - 2qzqw	2qxqz + 2qyqw
2qxqy + 2qzqw	1 - 2qx² - 2qz²	2qyqz - 2qxqw
2qxqz - 2qyqw	2qyqz + 2qxqw	1 - 2qx² - 2qy²

1 - 2(v1 x v2).y² - 2(v1 x v2).z²	2(v1 x v2).x(v1 x v2).y - 2(v1 x v2).z(1 + v1•v2)	2(v1 x v2).x(v1 x v2).z + 2(v1 x v2).y(1 + v1•v2)
2(v1 x v2).x(v1 x v2).y + 2(v1 x v2).z(1 + v1•v2)	1 - 2(v1 x v2).x² - 2(v1 x v2).z²	2(v1 x v2).y(v1 x v2).z - 2(v1 x v2).x(1 + v1•v2)
2(v1 x v2).x(v1 x v2).z - 2(v1 x v2).y(1 + v1•v2)	2(v1 x v2).y(v1 x v2).z + 2(v1 x v2).x(1 + v1•v2)	1 - 2(v1 x v2).x² - 2(v1 x v2).y²

導航

統計

常用鏈接

留言簿(27)

隨筆檔案(150)

文章檔案(1)

博客鏈接

搜索

積分與排名

最新評論

Maths - Angle between vectors

For 2D Vectors

For 3D Vectors

Axis Angle Result

Quaternion Result

Matrix Result

Code

Vector Dot Product

Vector Cross Product

Standards

Transforms

Beginning Game Writing