QM編碼器規則簡單介紹
QM 編碼器原理上是一種算術編碼器,但其將每個輸入的符號作單個的為來輸入(二進制位要么是 0 ,要么是 1 ),那么符號要么是 MPS (大概率符號),要么就是 LPS (小概率符號)。 QM 編碼器需要一個模型來首先預測下一位是 0 還是 1 ,然后再輸入該位來實際分類。
統計模型是用來計算
LPS
的概率
Qe
的,那么
MPS
的概率就是
1-Qe
。
Qe
是
LPS
的概率,通常情況
Qe
是小于等于
0.5
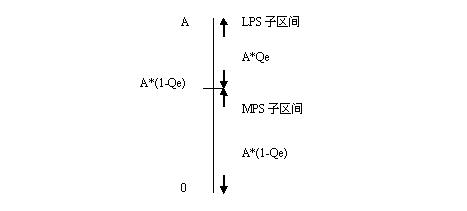
的;一般是將
LPS
的區間放在
MPS
區間的上邊;
A
表示整個區間。如下圖:
在 QM 編碼器中,使用符號 C ( code )表示輸出符號串。 QM 編碼器輸出的時候比普通的算術編碼器簡單,僅僅需要將 MPS 或 LPS 的區間下限增加到 C 中,因為這里之后兩個符號。一般 QM 的編碼規則是:
如果遇到一個 MPS , C = C+0 , A 變成原來 MPS 的子區間了; A = A * ( 1-Qe )
如果碰到一個 LPS ,需要將 LPS 區間的下限( A* ( 1-Qe )添加到 C 中;這個時候 A 變成原來 LPS 的子區間, A = A*Qe 。
具體規則如:
if MPS
{
?????? C 不變;
?????? A = A* ( 1-Qe );
}
else //LPS
{
?????? C = C+A*(1-Qe);
?????? A = A*Qe;
}
重定標之后的規則:
為了使用加法、減法和移位來模擬乘除,需要在 A 小于 0.75 的時候進行重定標,保證 A 與 1 比較接近而使用加、減的操作乘法差不大。這里使用 0 到 65536 之間的整數( 16 進制的 0x0000-0x10000 )表示小數 0 到 1.5 。
那么上面的規則變為:
如果遇到一個 MPS , C 不變, A 變成 MPS 的子區間; A = A-Qe (模擬乘法);但如果 A 小于 0.75(0x8000) 時,需要對 A 重定標, A 加倍, C 也加倍,直到 A 大于 0X8000 為止。
如果遇到一個 LPS , C 變為 C+A-Qe (模擬原來的乘法); A 變成 Qe (模擬乘法);由于 LPS 的區間始終小于等于 0.5 也就是小于 0.75 ,從而肯定要重定標 A 和 C ,同上。
簡單表示為:
if(MPS)
{
?????? A = A-Qe;
?????? while(A<0X8000)
?????? {
????????????? A <<=1;
????????????? C <<=1;
}
}
else//LPS
{
?????? C = C+A-Qe;
?????? A = Qe;
?????? While(A<0X8000)
?????? {
????????????? A<<=1;
????????????? A<<=1;
}
}
交換區間之后的規則:
由于使用加、減和移位來模擬乘法,導致有的時候 LPS 的區鍵會大于 MPS 的區間,這是也 QM 編碼器的初始條件相違背的;因此為了運算能夠繼續進行,這里對 LPS 和 MPS 的區間進行交換,從而保證運算規則仍然可以進行。這個時候的上面規則是:
如果遇到一個 MPS 后; C 仍然不變,首先將 A 設置為 MPS 的子區間( A = A-Qe )。這個時候需要檢查是否需要重定標,檢查原則同上,判斷 A 是否小于 0X8000 ;如果不需要重定標表示 A 大于 0X8000 ,那么這個時候 MPS 肯定大于 LPS ,不需要交換區間;如果需要重定標,檢查 A 是否小于 LPS 的區間 Qe ,如果小,表示需要交換區間;交換區間相當于取 LPS 的子區間,那么這個時候需要將 LPS 的區間下限輸出到 C 中,從而在解碼的時候做同樣的操作。
如果遇到一個 LPS 后;首先將 A 先設置為 MPS 的子區間( A = A-Qe )。按前面的推算,應該是 A 設置為 LPS 的子區間,所以這里增加了一個判斷 A 是否大于 LPS 的子區間,如果大表示我們取的是一個 MPS 的區間,和當前是 LPS 的不相符,因此應該取一個區間較小的值,也就是 LPS ,那么這個時候需要將 LPS 的下限輸入到 C 中,同時 A 等于 Qe 。但如果 A 小于 LPS 的子區間,表示 MPS 的區間比 LPS 的區間小,那么如果去 LPS 表示我們取了一個大概率符號的區間,那么和輸入一個 LPS 的情況不相符合,所以這種情況下,就去 A 為 MPS 的區間( A-Qe ),從而其下限是 0 ,那么 C 就不改變了。不管發生什么情況,如果輸入一個 LPS 符號,總是要重標的,同前面,直到 A>0x8000 為止。
簡單描述如下:
if(MPS)
{
?????? C = C+0;
?????? A = A-Qe;
?????? If(A<0X8000)
?????? {
????????????? if(A<Qe)
????????????? {
???????????????????? C = C+A;
???????????????????? A = Qe;
}
}
while(A<0X8000)
{
?????? A <<=1;
?????? C<<=1;
};
}
else//LPS
{
?????? A = A-Qe;
?????? If(A>=Qe)
?????? {
????????????? C = C+A;
????????????? A = Qe;
}
while(A<0X8000)
{
?????? A <<=1;
?????? C<< =1;
};
}
posted on 2006-08-12 23:41 笨笨 閱讀(3684) 評論(1) 編輯 收藏 引用 所屬分類: 壓縮算法


