使用微軟的D3D來編程需要熟悉3D幾何原理。本節介紹建立3D世界的最重要的幾何概念。
1.1.1. 3-D坐標系統
典型的3D圖形程序使用兩種笛卡兒坐標系統:左手和右手。兩個坐標系統中,正X軸指向右邊,正Y軸指向上。你可以通過你左右手指間指向與正X軸相同時大拇指指向的方向來記住坐標方向。下圖描述了這兩種系統。
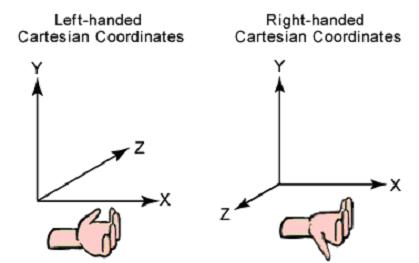
微軟的D3D使用左手系統,如果你正在將一個基于右手坐標系統的程序導入到程序中,你必須做兩個改變過度到D3D。
1.1.2. 3-D原基(點陣)
一個3D原基就是一個形成單個3D實體的頂點集合。最簡單的原基是3D系統中點的集合,也叫做點列表。
當然,3D原基是多邊形。一個多邊形是一個至少包括3個頂點的封閉的圖形。最簡單的多邊形是3角形。微軟D3D使用三角形來組成大多數的多邊形,因為三角形中的三個頂點是共面的,渲染不是平面的頂點是無效的。你可以通過合并三角形來形成大的、復雜的多邊形和網格。
下圖描述了一個立方體。正方體的每個面由2個三角形組成,所有三角形形成一個正方體原始。你能使用材質和原料到原始的每個面上來使他們看起來象一個固體形狀。

你也可以用三角形來建立表面平滑的平面。下面的圖顯示了一個使用三角形來仿真的球體;在應用材料以后,在渲染的時候球體看起來平滑很多。如果你使用Gouraud陰影,更是這樣。詳細的細節參見Gouraud 陰影。
1.1.3. 面和頂點法線向量
網格中的每個面都有一個正交的法線向量。向量的方向是由頂點定義的順序和左右手坐標系統。正面法線從正面的前邊指出。微軟的D3D系統,僅僅正面的前邊是可見的,前面就是頂點以順時針方向定義的面。
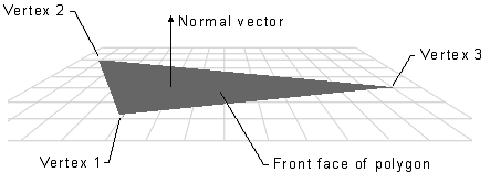
D3D使用頂點法線來表示陰影、光線和材質效果。
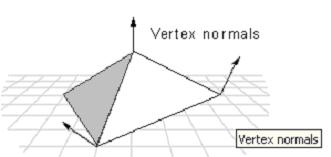
在一個多邊形上應用陰影時,D3D使用頂點法線來計算光源和表面之間的角度。其為頂點計算色彩和亮度值,并且通過所有原始表面來為每個頂點加入。D3D通過角度來計算光亮度值。角度越大,亮度越小。
如果你正在一個平面上創建一個對象,設置頂點法線來指向表面的垂線,就如下圖所示。定義一個由兩個三角形組成的平面。
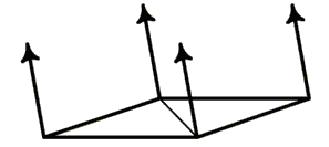
然而,很可能你的對象有一些不共面條的三角形組成;為了獲得通過所有三角形帶的平滑陰影,一個簡單的辦法就是首先計算與頂點相關的每個多邊形曲面法線矢量。頂點法線被設置為對于每個曲面法線有相同的角度。但這個方法在復雜的初基(點陣)并不是特別有效。
上面的方法通過下圖來描述,他展示了兩個曲面,S1和S2有一條邊相交。S1和S2的法線使用藍色表示。頂點法線矢量用紅色顯示。頂點法線矢量和S1和S2面上的曲面法線角度一樣。當這兩個表面被點亮或使用Gouraud陰影,結果在他們之間是一個平滑的陰影,平滑的圓形邊。
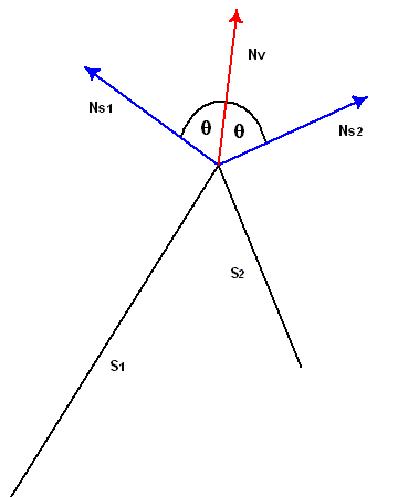
如果頂點發現朝其中關聯的一個面傾斜,它導致指向表面的光強度增加或降低,主要依賴于和光源之間的角度。下面表明這個例子。同樣,這些面是邊相交的,頂點法線向S1傾斜導致其和光源之間角度較小。
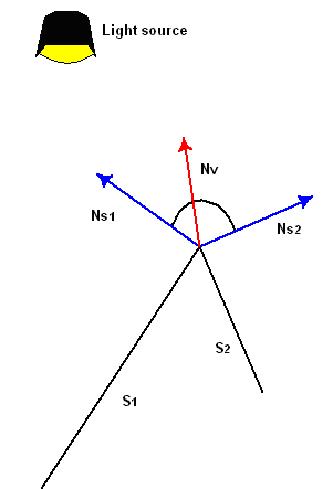
你可以使用Gouraud陰影來在3D場景中顯示一些帶有明顯邊的對象,為了這么做,需要在每個明顯邊緣的面相交處復制頂點法線矢量,如下圖顯示:
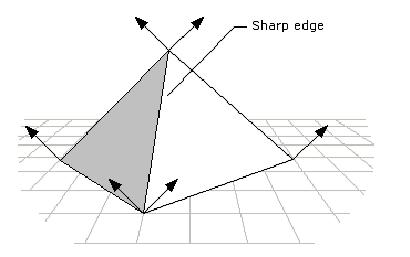
如果你使用DrawPrimitive方法來粉刷你的場景,定義帶有明顯邊界的對象作為一個三角形列表而不是三角形帶。當你定義一個作為三角形帶的對象,D3D將其作為一個由多個三角形面組成的單個多邊形。Gouraud陰影應用到通過多邊形每個面以及相鄰面之間;結果是具有從一個面到另一個面平滑陰影的對象;因為一個三角形列是一系列分解三角形面組成的一個多邊形,D3D使用Gouraud陰影貫穿多邊形的每個面;然而,它并不應用到面到面,如果兩個或多個三角形列中的三角形相鄰,在他們之間會有一個明顯的邊界。
另外在粉刷一個帶有明顯邊界的對象時選擇是將其作為平面陰影。這是最有效的方法,但他可能導致一個對象沒有使用Gouraud陰影粉刷理想的效果。
1.1.4. 光柵化規則
經常,指定的頂點并不正好和屏幕上的像素相匹配;當這個發生的時候,D3D使用三角形光柵化原則來那些像素對應到給定的三角形上。
1. 三角形光柵化原則
2. 點和線規則
3. 點精靈規則
1.1.4.1.1. 三角形光柵化規則
D3D使用頂-左填充約定作為填充幾何算法。這同微軟GDI以及OpenGL的矩形填充約定相同。在D3D中,像素的中央是決定性點,如果中心在一個三角形中,那這個像素是三角形的一部分。像素中心是整數坐標。
這個D3D使用的三角形光柵化原則并不是必須應用到所有可用的硬件上;你的測試或許揭示這些規則小的變化。
下圖顯示一個左上角在(0,0)點的矩形,其右下角在(5,5)點;這個舉行填充了25個像素,就像你預期的一樣,矩形的寬度定義為右-左,高度是底減去頂部。
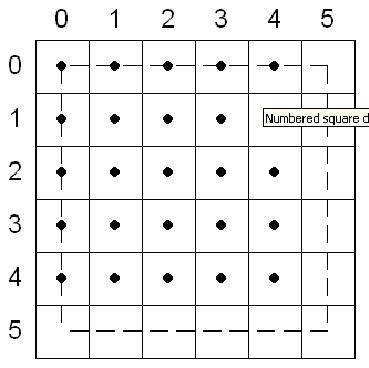
在頂左填充約定中,頂指的是水平跨度的垂直位置,左指的是一個像素寬度的水平位置。一個邊不能是頂邊,除非它是水平的;通常大多數三角形有唯一的左和右邊。
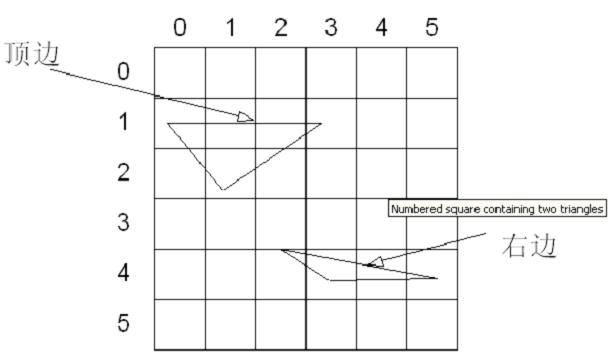
頂-左填充約定決定了當一個三角形穿過一個像素中心時D3D的行為。下圖展示了兩個三角形,一個是(0,0),(5,0),(5,5);而另外一個在(0,5),(0,0),(5,5)。這個例子中第一個三角形得到15個像素(黑色顯示),然而第二個得到10個像素(灰色顯示),因為他們共享邊是第一個三角形的左邊邊。
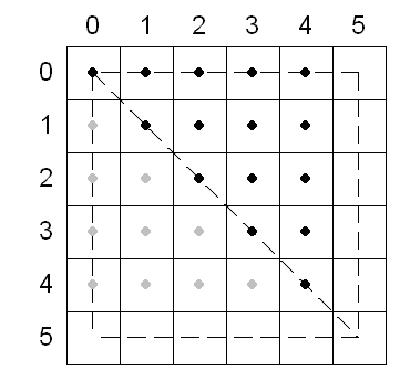
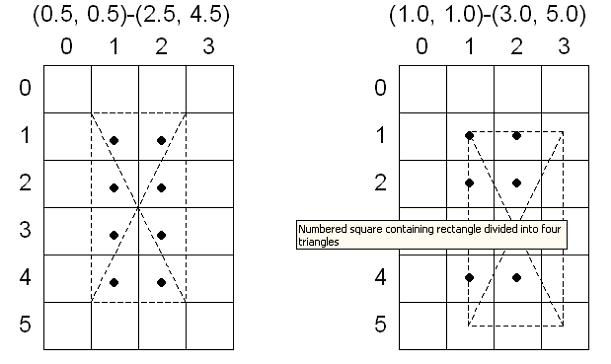
如果你定義一個矩形其左上角在(0.5,0.5),右下角在(2.5,4.5),中心點是(1.5,2.5)。當D3D光柵 tesselate這個矩形時,每個像素的中心都明顯的在矩形的內部,且左上角填充規則不必要。下圖說明這個內容;矩形中的像素依據D3D包括的三角形標記。
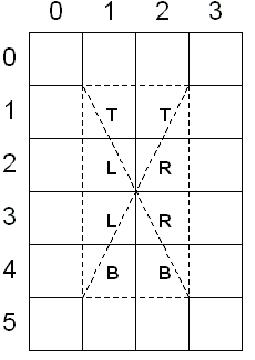
如果你移動上面例子中的矩形使其左上角坐標在(1.0,1.0),它的右下角在(3.0,5.0),它的中心點在(2.0,3.0),D3D使用左上填充約定;大多數三角形在兩個或多個三角形的邊界上,如下圖所示:
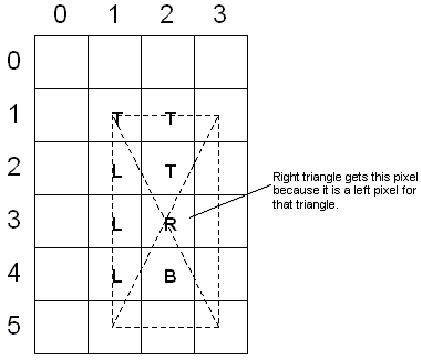
兩個矩形中,影響的相同像素如下:
1.1.4.1.2. 點和線規則
點和點精靈粉刷方式是相同的,他們都依照屏幕對齊的四邊形方式粉刷,從而和多邊形粉刷具有相同的規則。
Non-antialiased線粉刷方式同GDI相同。
更多關于antialiased線的粉刷,見ID3DXLine。
1.1.4.1.3. 精靈點規則
精靈點和補丁初基首先被鑲嵌到三角形中,然后使用結果三角形光柵化原則來處理;更多的信息參見:精靈點。
1.1.5. 矩形
貫穿D3D和Windows編程,屏幕上的對象都歸諸于范圍矩形。矩形的邊同屏幕的邊平行,因此舉行可以使用兩個點來表示,左上角和右下角。大多數程序在blitting到屏幕上或執行hit檢測的時候使用攜帶矩形信息的RECT結構。
在C++中,RECT結構定義如下:
typedef struct tagRECT { LONG left; // This is the upper-left corner x-coordinate.
LONG top; // The upper-left corner y-coordinate.
LONG right; // The lower-right corner x-coordinate.
LONG bottom; // The lower-right corner y-coordinate.
} RECT, *PRECT, NEAR *NPRECT, FAR *LPRECT;
前面的例子中,left和top成員指的是矩形左上角的x和y坐標,同樣right和bottom指的是右下角的x和y的坐標。下圖描述了你怎么形象化的理解這些值。
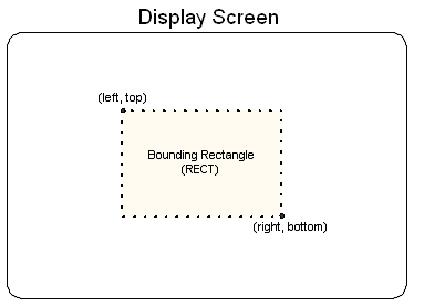
為了效率、一致性和容易使用的目的,所有D3D顯示函數都使用矩形來工作。
1.1.6. 三角形Interpolants
在粉刷過程中,管道插入穿過每個三角形的頂點數據;頂點數據可以明顯的變化并包含(但不限制于)彌漫的色彩、有金屬光澤的色彩、彌漫的alpha(三角形通明性)、金屬光澤alpha和霧化因素(為頂點管道降低金屬光澤alpha以及降低可編程頂點管道霧化登記);這個頂點數據被定義為頂點聲明。
對于許多頂點數據來說,插入獨立于當前的陰影模式,如下表描述:
|
陰影模式 |
描述 |
|
平面 |
僅僅霧化因素被插入到平面陰影模式中;對于所有其他的插入,第一個頂點的顏色將應用為穿過整個面的色彩 |
|
Gouraud |
在所有三個頂點之間執行線性插入 |
彌漫色彩和金屬光澤色彩不同對待,依賴于顏色模式。在RGB模式中,系統在插入中使用紅、綠、藍成分。
色彩的Alpha成分作為一個單獨的interpolant對待,因為設備驅動可以用兩種方法來實現通明性:使用材質混合或使用點畫法。
使用D3DCAPS9結構體的ShadeCaps成員來決定當前設備驅動支持什么樣的interpolation形式。
1.1.7. 矢量、頂點和四元數
貫穿D3D,頂點描述位置和方向;初基中的每個點被描述為一個具有位置、顏色、材質坐標和給定方向的法線向量的一個向量。
四元數添加一個元素到[x ,y ,z]值中來定義一個三分量矢量。四元數是3D旋轉時使用的矩陣方法的另一個選擇;一個四元數表達一個3D平面的軸以及繞軸旋轉的度。例如:四元數可能表示一個(1,1,2)軸和一個1弧度的旋轉。四元數攜帶重要的信息,但他們真正的作用來自兩個你可以執行的操作:組合和插入(interpolation)。
在一個四元數上執行合成操作和合并他們很相似,兩個四元數的合成標記為:
Q=q1Oq2
兩個四元數的合成應用到幾何學上意味著:繞軸2旋轉幾何圖形旋度2,然后繞軸1旋轉旋度1;這個例子中,Q表示一個繞一個軸的旋轉角度,也是作用q2然后q1到幾何圖形上的結果。
使用四元數interpolation,程序可以從一個軸和方向計算到另一個的平滑的和合理的路徑。因此,在q1和q2之間的interpolation為從嚴格方向到另一個方向提供了動畫的簡單方法。
當你一起使用組合和interpolation時候,他們為你以看起來很復雜的方式操作一個幾何圖形提供了一個簡單的方法。例如,你想旋轉一個圖像到給定的方向,你知道繞軸2旋轉r2角度,然后繞軸1旋轉r1角度,但你不知道最終的四元數,通過使用組合,你能夠合并兩個旋轉為一個單一的四元數,然后,你能夠從原來的點到組合四元數interpolate來得到一個平滑的轉換。
D3D擴展(D3DX)工具庫包含使用四元數的函數,例如:D3DXQuaternionRatationAxis為一個向量添加一個旋轉值,其返回一個D3DXQUATERNION結構體四元數結果。另外,D3DXQuaternionMultiply函數組合四元數,D3DXQuaternionSlerp在兩個四元數之間執行球形線性interpolation。
D3D程序能使用下面函數來簡化四元數的工作:
D3D程序可以使用下面的函數來簡化三成分向量的工作: