高斯消元
算法目的:
高斯消元,一般用于求解線性方程組AX = B(或 模線性方程組AX mod P = B),以四個未知數,四個方程為例,AX=B表示成4x4的矩 陣和4x1的矩陣相乘的形式:
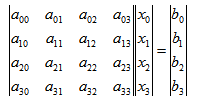
其中A和B(b0 b1 b2 b3)已知,要求列向量X(x0 x1 x2 x3)的值。
算法核心思想:
對于n個方程,m個未知數的方程組,消元的具體步驟如下:
1、枚舉第i (0 <= i < n) 行,初始化列為col = 0,每次從[i, n)行中找到第col列中元素絕對值最大的行和第i行進行交換(找到最大的行是為了在消元的時候把浮點數的誤差降到最小);
a) 如果第col列的元素全為0,放棄這一列的處理,col+1,i不變,轉1);
b) 否則,對于所有的行j (i < j < n),如果a[j][col]不為0,則需要進行消元,以期第i行以下的第col列的所有元素都消為0(這一步就是線性代數中所說的初等行變換,具體的步驟就是將第j行的所有元素減去第i行的所有元素乘上一個系數,這個系數即a[j][col] / a[i][col])。
2、重復步驟1) 直到n個方程枚舉完畢或者列col == m。
3、判斷解的情況:
a) 如果出現某一行,系數矩陣全為0,增廣矩陣不全為0,則無解(即出現[0 0 0 0 0 b],其中b不等于0的情況);
b) 如果是嚴格上三角,則表明有唯一解;
c) 如果增廣矩陣有k (k > 0)行全為0,那么表明有k個變量可以任意取值,這幾個變量即自由變量;對于這種情況,一般解的范圍是給定的,令解的取值有T個,自由變量有V個,那么解的個數就是 TV。
算法復雜度:
O(n3)
ACM中的高斯消元題型一般涉及到的有:
1、浮點數消元
系數矩陣為整數或浮點數,消元的時候乘上的系數為浮點數,一般用于求解浮點數解,例如HDU 3359;
2、整數消元
系數矩陣全為整數,消元的時候乘上的系數均為整數,整個消元過程不出現浮點數。由于乘法很容易溢出,一般很少用。
3、模線性方程組
系數矩陣全為整數,消元的時候乘上的系數均為整數,每次運算都模上一個數P,整個消元過程不出現除法,最后求解的時候用線性同余迭代求解,一般題型較多,有的是給定解的范圍,求解的數量,例如:PKU 1830、HDU 3364;有的是求一個解,例如PKU 2065、HDU 3571;有的是求解的存在性,例如PKU1288、PKU 3185。
提供一個自己寫的模線性方程的高斯消元模板:
1 #define MAXN 105
2 #define LL __int64
3 4 /*
5 高斯消元 - 同余方程
6 一般只要求求一個解/而且必然有解
7 */ 8 9 LL GCD(LL a, LL b) {
10 if(!b) {
11 return a;
12 }
13 return GCD(b, a%b);
14 }
15 16 LL ExpGcd(LL a, LL b, LL &X, LL &Y) {
17 LL q, temp;
18 if( !b ) {
19 q = a; X = 1; Y = 0;
20 return q;
21 }
else {
22 q = ExpGcd(b, a % b, X, Y);
23 temp = X;
24 X = Y;
25 Y = temp - (a / b) * Y;
26 return q;
27 }
28 }
29 30 LL Mod(LL a, LL b, LL c) {
31 if(!b) {
32 return 1 % c;
33 }
34 return Mod(a*a%c, b/2, c) * ( (b&1)?a:1 ) % c;
35 }
36 37 class GaussMatrix {
38 public:
39 int r, c;
40 LL d[MAXN][MAXN];
41 LL x[MAXN];
// 某個解集
42 LL xcnt;
// 解集個數
43 44 LL abs(LL v) {
45 return v < 0 ? -v : v;
46 }
47 48 void swap_row(
int ra,
int rb) {
49 for(
int i = 0; i <= c; i++) {
50 LL tmp = d[ra][i];
51 d[ra][i] = d[rb][i];
52 d[rb][i] = tmp;
53 }
54 }
55 void swap_col(
int ca,
int cb) {
56 for(
int i = 0; i < r; i++) {
57 LL tmp = d[i][ca];
58 d[i][ca] = d[i][cb];
59 d[i][cb] = tmp;
60 }
61 }
62 63 void getAns(LL mod) {
64 for(
int i = c-1; i >= 0; i--) {
65 LL tmp = d[i][c];
66 // d[i][i] * x[i] + (d[i][i+1]*x[i+1] +  + d[i][c]*x[c]) = K*mod + tmp;
+ d[i][c]*x[c]) = K*mod + tmp;
67 for(
int j = i+1; j < c; j++) {
68 tmp = ((tmp - d[i][j] * x[j]) % mod + mod) % mod;
69 }
70 // d[i][i] * x[i] = K * mod + tmp;
71 // d[i][i] * x[i] + (-K) * mod = tmp;
72 // a * x[i] + b * (-K) = tmp;
73 LL X, Y;
74 ExpGcd(d[i][i], mod, X, Y);
75 x[i] = ( (X % mod + mod) % mod ) * tmp % mod;
76 }
77 }
78 79 // -1 表示無解
80 LL gauss(LL mod) {
81 int i, j, k;
82 int col, maxrow;
83 84 // 枚舉行,步進列
85 for(i = 0, col = 0; i < r && col < c; i++) {
86 //debug_print();
87 maxrow = i;
88 // 找到i到r-1行中col元素最大的那個值
89 for(j = i+1; j < r; j++) {
90 if( abs(d[j][col]) > abs(d[maxrow][col]) ){
91 maxrow = j;
92 }
93 }
94 // 最大的行和第i行交換
95 if(maxrow != i) {
96 swap_row(i, maxrow);
97 }
98 if( d[i][col] == 0 ) {
99 // 最大的那一行的當前col值 等于0,繼續找下一列
100 col ++;
101 i--;
102 continue;
103 }
104 105 for(j = i+1; j < r; j++) {
106 if( d[j][col] ) {
107 // 當前行的第col列如果不為0,則進行消元
108 // 以期第i行以下的第col列的所有元素都消為0
109 LL lastcoff = d[i][col];
110 LL nowcoff = d[j][col];
111 for(k = col; k <= c; k++) {
112 d[j][k] = (d[j][k] * lastcoff - d[i][k] * nowcoff) % mod;
113 if (d[j][k] < 0) d[j][k] += mod;
114 }
115 }
116 }
117 col ++;
118 }
119 // i表示從i往后的行的矩陣元素都為0
120 // 存在 (0 0 0 0 0 0 d[j][c]) (d[j][c] != 0) 的情況,方程無解
121 for(j = i; j < r; j++) {
122 if( d[j][c] ) {
123 return -1;
124 }
125 }
126 // 自由變元數 為 (變量數 - 非零行的數目)
127 int free_num = c - i;
128 129 // 交換列,保證最后的矩陣為嚴格上三角,并且上三角以下的行都為0
130 for(i = 0; i < r && i < c; i++) {
131 if( !d[i][i] ) {
132 // 對角線為0
133 for(j = i+1; j < c; j++) {
134 // 在該行向后找第一個不為0的元素所在的列,交換i和這一列
135 if(d[i][j])
break;
136 }
137 if(j < c) {
138 swap_col(i, j);
139 }
140 }
141 }
142 xcnt = ( ((LL)1) << (LL)free_num );
143 144 getAns(mod);
145 return xcnt;
146 }
147 148 void debug_print() {
149 int i, j;
150 printf("-------------------------------\n");
151 for(i = 0; i < r; i++) {
152 for(j = 0; j <= c; j++) {
153 printf("%d ", d[i][j]);
154 }
155 puts("");
156 }
157 printf("-------------------------------\n");
158 }
159 };
160 來看幾道經典的高斯消元,熟悉各種類型的高斯消元。
HDU 3359 Kind of a Blur
題意:H * W (W,H <= 10) 的矩陣A的某個元素A[i][j],從它出發到其他點的曼哈頓距離小于等于D的所有值的和S[i][j]除上可達點的數目,構成了矩陣B。給定矩陣B,求矩陣A。
題解:將所有矩陣A的元素看成自變量,一共有H*W個變量,每個矩陣B的元素是由這些變量組合而成的,對于固定的B[i][j],曼哈頓距離在D以內的A[x][y]的系數為1,其它為0,這樣就變成了求H*W個變量和H*W個方程的線性方程組,高斯消元求解。這題數據量比較小,所以直接采用浮點數的高斯消元即可,需要注意的是,浮點數消元的時候為了避免精度誤差,每次找最大的行,乘上一個小于1的系數進行消元,這樣可以把誤差降到最小。
PKU 1830 開關問題
題意:給定N(N < 29)個開關,每個開關打開和關閉的時候會引起另外一個開關的變化,本來為打開的會變成關閉,本來關閉的會變成打開。給定N個開關的初始狀態和終止狀態,以及關聯的開關關系,求共有多少種方案從初始狀態變成終止狀態(不計順序,并且每個開關只能操作至多一次)。
題解:由于開關只有打開和關閉兩種狀態,所以對于每個開關的打開和關閉,組合一下總共有2^N種情況,枚舉所有情況判可行性,對于這個數據量來說是不現實的,需要想辦法優化。
我們用X[i]來表示第i個開關的操作狀態(1表示操作,0表示不操作)。
第i個開關會被哪些開關影響是可以知道的(這個關系在輸入的時候會給出),假設影響第i個開關的開關列表為L[i][0], L[i][1], L[i][2]... 第i個開關的起始狀態為S[i],終止狀態為E[i],則可以列出N個方程:
( X[0] * A[i][0] + X[1] * A[i][1] + ... + X[n-1] * A[i][n-1] ) % 2 = (E[i] - S[i]);
每個方程代表一個開關被它本身以及它的關聯開關操作后的最終狀態,系數矩陣A[i][j]代表了開關之間的連帶關系:
1) 如果第j個開關的操作能夠影響第i個開關的狀態,那么A[i][j] = 1;
2) 如果第j個開關的操作不影響第i個開關的狀態,那么A[i][j] = 0;
3) 特殊的A[i][i] = 1(開關本身的操作必然會影響自己的當前狀態);
X[i]取值為0或1,這樣就是N個N元一次方程組,利用高斯消元求解即可。將增廣矩陣化簡為上三角的形式后,剩余全為0的行的個數為自由變元的個數F(自由變元就是它在取值范圍內可以取任意值,這題是個方陣,所以自由變元的個數等于全為0的行的個數),所以,由于開關一共兩種狀態,取值為0和1,所以總的解的個數為2^F。特殊的,如果某一行系數全為零,而增廣矩陣最后一列對應行的值不為0,則表示無解。
HDU 3364 Lanterns
PKU 1830的簡單變種。那題是用開關來控制開關,這題是用開關來控制燈,而且開關和燈的數目是不一樣的,這樣就導致了高斯矩陣并不是一個方陣,而是一個N*M的矩陣,
同樣的構造系數矩陣的方法,當N和M不相等的情況下,自由變元的個數就不是剩余全為0的行的個數了。其實對于一般的方程,自由變元的個數為 Free =(變量數var - 非0系數向量的個數)。這題數據量比那題大,最大情況有可能是2^N,所以需要用__int64。
PKU 2065 SETI
題意:
(a1 * 10 + a2 * 11 + ... an * 1n) % P = C1
(a1 * 20 + a2 * 21 + ... an * 2n) % P = C2
(a1 * 30 + a2 * 31 + ... an * 3n) % P = C3
....
(a1 * n0 + a2 * n1 + ... an * nn) % P = Cn
給定n個以上的方程組,求滿足條件的 ai (1 <= i <= n)。
題解:如果沒有模 P,那么這個就是N個N元一次方程組,利用高斯消元可以求解,加上模P剩余后,其實原理一樣,只不過在初等行變換后,每次進行消元的時候將所有值模P,最后求解回帶的時候利用擴展歐幾里得來對每一個ai求一個最小的可行解。
例如,最后化簡的行階梯陣如下圖:
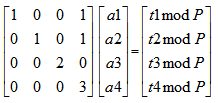
那么從后往前進行迭代求解的時候,必然會遇到兩個數相乘模P等于一個常數的情況,比如求a4的時候,有同余數方程 3*a4 % P = t4,可以表示成3*a4 + K*P = t4,其中P必然和3互素(題中有說明),所以這個方程必然有解,利用擴展歐幾里得可以求得一個最小的非負整數a4,a4求出后同理求出a3、a2、a1即可。
PKU 3185 The Water Bowls
題意:20個開關排成一排,兩邊的開關的開啟和關閉狀態會帶動相鄰的一個開關,中間的開關的開啟和關閉會帶動相鄰的兩個開關,問給定一個狀態能否將這些開關的狀態都變為打開狀態,如果能輸出最小的操作次數。
題解:PKU 1830的變種,求最小的操作次數就是求所有解集中解的總和最小的解集,所以在進行初等行變換之后,利用dfs來枚舉所有的解,當然如果不是自由變元的,解是確定的,由于開關開兩次和不操作是一樣的,所以每個開關的解集為{0, 1},枚舉過程中記錄當前操作的次數,如果比之前記錄的最小操作次數大,那么無須往下枚舉,直接返回,作為剪枝。由于狀態最多220種,加上適當的剪枝,可以很快把解搜出來。
HDU 3571 N-dimensional Sphere
題意:在一個N維空間中,給定一個N+1個點,求一個點使得它到所有點的距離都為R(R不給出),保證解為整數,并且解的范圍為 [-1017, 1017]。
題解:對于N個未知數,N+1個方程,相鄰兩個方程相減可以把二次項全部約去,剩下一次項系數,則問題轉化為N個未知數,N個方程的一次方程組,可以利用高斯消元求解,但是這題的數據量比較大,最大的可能解為1017,如果利用大數,乘法的復雜度很高,可以采用同余的方法,所以所有加法、減法、乘法需要模一個大的素數(需要大于1017的素數,可以利用拉賓米勒算法隨機生成一個大素數P),然后利用同余方程求一個最小的非負數解,在進行相乘運算的時候最大情況會超過int64,所以處理乘法運算的時候需要用到二分加法,所有的乘模運算需要化簡成加法和減法運算。利用PKU 2065 的求法可以求得所有可行解,由于這題的數據量可能為負數,同余的情況下求出來的是非負數,為了消除這種情況,對所有輸入的值加上一個偏移量1017,最后的解再減去這個偏移量,注意最后的答案減去偏移量的時候不需要取模(否則就沒有意義了)。
PKU 1288 Sly Number
題意:定義Sly Number為只有{0, 1, 2}三種數字的一維數組,對于兩個Sly Number:A 和B的乘法操作如下:

圖1
相乘后的取余操作如下:
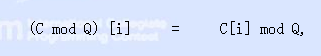
圖2
定義ONE為A[0] = 1, A[i] = 0 (i = 1, 2, ...N-1),給定A和Q,求A對于Q的逆元,即(A * B) mod Q = ONE中的B。
題解:首先B也是Sly Number,結合圖中的等式,可以列出N個方程:
C[0] = (A[0]*B[0]) + ( A[1]*B[N-1] + A[2]*B[N-2] + ... + A[N-1]*B[1]) ;
C[1] = (A[0]*B[1] + A[1]*B[0]) + ( A[2]*B[N-1] + ... + A[N-1]*B[2] );
...
C[N-1] = (A[0]*B[N-1] + A[1]*B[N-2] +... A[N-1]*B[0]);
由模的定義,可知C[0] mod Q = 1, C[i] mod Q = 0 (i = 1, 2, ... N-1)
于是可以列出N個方程N個未知數的模線性方程組,利用圖1的下標關系,將A[i]填入對應的系數矩陣中,用高斯消元化解增廣矩陣為上三角梯陣,然后從N-1到0枚舉B[i] 的取值(取值為0、1、2),當B[i](0 < i < N)滿足條件則遞歸枚舉B[i-1],知道所有的B[i]枚舉完畢,則表明至少有一個解,否則無解。
SGU 173 Coins
題意:N(2 <= N <= 50)個硬幣排成一排,有的人頭朝上(用0表示),有的則是字朝上(用1表示),對這一排硬幣進行M(1 <= M <= 10)次X變換之后的狀態已知,求初始的硬幣狀態。
定義一次X變換如下:
1、從這一排硬幣的Si(1 <= Si <= N, 1<= i <= M)位置取連續的K(2 <= K <= N)個硬幣;
2、對這取出來的K個硬幣進行一次循環左移操作;
3、掃描前K-1個硬幣,如果第i個硬幣字朝上(即為1),并且Ai等于1,那么將第K個硬幣進行一次翻轉;
4、重復2) - 3) 操作Di(Di <= 106)次;
上述X變換的3)中出現了Ai,但是題目并未給出Ai ( 1 <= i <= K-1),而是給出了L(L <= 200)個X變換之前的狀態和之后的狀態(每個狀態為K個硬幣),需要利用這L條關系來求出Ai,并且題目保證Ai有且僅有一個解。
題解:題目兜兜轉轉繞了一大圈,實在很難讀懂,只能通過樣例來琢磨意思。這個題目分為兩部分,首先是要把Ai求出來,然后再根據Ai的值和結束狀態反推初始狀態。
首先來看樣例,L = 2, K = 3 兩組X變換的前后狀態為010 -> 101、101 -> 011。
對于第一對狀態,010循環左移后為100,第K個硬幣和結束狀態不相符,說明前2(即K - 1)個硬幣中字朝上的硬幣對應的Ai必定有奇數個為1(這樣才能使第K個硬幣從0翻轉到1),而前二個硬幣只有第一個為1,所以A1 = 1;同理對于第二個狀態,可以求出A2 = 0;
模擬一下樣例可以大致了解題目的用意,但是對于一般的情況還是需要用系統的方法去分析,讓我們來看下一般的情況,對于某一對狀態如下:
初始狀態S = S1S2S3...SK-1SK 結束狀態T = T1T2T3...TK-1TK
將初始狀態循環左移一次后為S’ = S2S3...SK-1SKS1,由于循環左移之后前K-1個硬幣的狀態不會再發生改變,所以有 S2S3...SK-1SK == T1T2T3...TK-1,當然這一點,題目數據是會保證的,我們不需要關心,我們需要關心的就是S1和TK 是否相等,如果S1和TK 相等,那么前T1T2T3...TK-1 中為1的對應的Ai=1的個數為偶數個,否則為奇數個。利用更加通俗的解釋,即(T1 A1 + T2 A2 + T3A3 + ...+ TK-1AK-1) mod 2 = S1 ^ TK,這個方程中,只有Ai是未知數,那么對于L個條件,我們可以列出L條方程,這樣就轉變成了L個方程K-1個未知數的模線性方程組,可以利用高斯消元求解Ai。
Ai求出來后,給定一個結束狀態,模擬M*Di次逆向操作,每次操作需要進行字符串的右移(因為是逆向,所以要和題目的左移相反)操作,每次右移最多牽涉N次原子操作,所以總的復雜度為O(N*M*Di),復雜度過大,但是注意到這里的N <= 50,所以我們可以將每個狀態壓縮到一個int64的整數中,A1A2A3..AK-1也可以壓縮成一個int64的整數,右移操作可以通過位運算在O(1)的時間內解決。其中有一步會涉及到判斷一個數的二進制表示中有多少個1的問題,網上各種面試題很多,不再累述,比較方便、效率也還可以的是采用樹狀數組中lowbit的思想,即利用 x 減去 (x&(-x)) (其中 x&(-x) = 2^k, k為x二進制末尾0的個數),逐個將1消去,直到x = 0為止,迭代消去的次數就是1的個數。