高斯消元
高斯消元
算法目的:
高斯消元,一般用于求解線性方程組AX = B(或 模線性方程組AX mod P = B),以四個未知數(shù),四個方程為例,AX=B表示成4x4的矩 陣和4x1的矩陣相乘的形式:
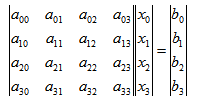
其中A和B(b0 b1 b2 b3)已知,要求列向量X(x0 x1 x2 x3)的值。
算法核心思想:
對于n個方程,m個未知數(shù)的方程組,消元的具體步驟如下:
1、枚舉第i (0 <= i < n) 行,初始化列為col = 0,每次從[i, n)行中找到第col列中元素絕對值最大的行和第i行進行交換(找到最大的行是為了在消元的時候把浮點數(shù)的誤差降到最小);
a) 如果第col列的元素全為0,放棄這一列的處理,col+1,i不變,轉(zhuǎn)1);
b) 否則,對于所有的行j (i < j < n),如果a[j][col]不為0,則需要進行消元,以期第i行以下的第col列的所有元素都消為0(這一步就是線性代數(shù)中所說的初等行變換,具體的步驟就是將第j行的所有元素減去第i行的所有元素乘上一個系數(shù),這個系數(shù)即a[j][col] / a[i][col])。
2、重復(fù)步驟1) 直到n個方程枚舉完畢或者列col == m。
3、判斷解的情況:
a) 如果出現(xiàn)某一行,系數(shù)矩陣全為0,增廣矩陣不全為0,則無解(即出現(xiàn)[0 0 0 0 0 b],其中b不等于0的情況);
b) 如果是嚴(yán)格上三角,則表明有唯一解;
c) 如果增廣矩陣有k (k > 0)行全為0,那么表明有k個變量可以任意取值,這幾個變量即自由變量;對于這種情況,一般解的范圍是給定的,令解的取值有T個,自由變量有V個,那么解的個數(shù)就是 TV。
算法復(fù)雜度:
O(n3)
ACM中的高斯消元題型一般涉及到的有:
1、浮點數(shù)消元
系數(shù)矩陣為整數(shù)或浮點數(shù),消元的時候乘上的系數(shù)為浮點數(shù),一般用于求解浮點數(shù)解,例如HDU 3359;
2、整數(shù)消元
系數(shù)矩陣全為整數(shù),消元的時候乘上的系數(shù)均為整數(shù),整個消元過程不出現(xiàn)浮點數(shù)。由于乘法很容易溢出,一般很少用。
3、模線性方程組
系數(shù)矩陣全為整數(shù),消元的時候乘上的系數(shù)均為整數(shù),每次運算都模上一個數(shù)P,整個消元過程不出現(xiàn)除法,最后求解的時候用線性同余迭代求解,一般題型較多,有的是給定解的范圍,求解的數(shù)量,例如:PKU 1830、HDU 3364;有的是求一個解,例如PKU 2065、HDU 3571;有的是求解的存在性,例如PKU1288、PKU 3185。
提供一個自己寫的模線性方程的高斯消元模板:
2 #define LL __int64
3
4 /*
5 高斯消元 - 同余方程
6 一般只要求求一個解/而且必然有解
7 */
8
9 LL GCD(LL a, LL b) {
10 if(!b) {
11 return a;
12 }
13 return GCD(b, a%b);
14 }
15
16 LL ExpGcd(LL a, LL b, LL &X, LL &Y) {
17 LL q, temp;
18 if( !b ) {
19 q = a; X = 1; Y = 0;
20 return q;
21 }else {
22 q = ExpGcd(b, a % b, X, Y);
23 temp = X;
24 X = Y;
25 Y = temp - (a / b) * Y;
26 return q;
27 }
28 }
29
30 LL Mod(LL a, LL b, LL c) {
31 if(!b) {
32 return 1 % c;
33 }
34 return Mod(a*a%c, b/2, c) * ( (b&1)?a:1 ) % c;
35 }
36
37 class GaussMatrix {
38 public:
39 int r, c;
40 LL d[MAXN][MAXN];
41 LL x[MAXN]; // 某個解集
42 LL xcnt; // 解集個數(shù)
43
44 LL abs(LL v) {
45 return v < 0 ? -v : v;
46 }
47
48 void swap_row(int ra, int rb) {
49 for(int i = 0; i <= c; i++) {
50 LL tmp = d[ra][i];
51 d[ra][i] = d[rb][i];
52 d[rb][i] = tmp;
53 }
54 }
55 void swap_col(int ca, int cb) {
56 for(int i = 0; i < r; i++) {
57 LL tmp = d[i][ca];
58 d[i][ca] = d[i][cb];
59 d[i][cb] = tmp;
60 }
61 }
62
63 void getAns(LL mod) {
64 for(int i = c-1; i >= 0; i--) {
65 LL tmp = d[i][c];
66 // d[i][i] * x[i] + (d[i][i+1]*x[i+1] +
 + d[i][c]*x[c]) = K*mod + tmp;
+ d[i][c]*x[c]) = K*mod + tmp;67 for(int j = i+1; j < c; j++) {
68 tmp = ((tmp - d[i][j] * x[j]) % mod + mod) % mod;
69 }
70 // d[i][i] * x[i] = K * mod + tmp;
71 // d[i][i] * x[i] + (-K) * mod = tmp;
72 // a * x[i] + b * (-K) = tmp;
73 LL X, Y;
74 ExpGcd(d[i][i], mod, X, Y);
75 x[i] = ( (X % mod + mod) % mod ) * tmp % mod;
76 }
77 }
78
79 // -1 表示無解
80 LL gauss(LL mod) {
81 int i, j, k;
82 int col, maxrow;
83
84 // 枚舉行,步進列
85 for(i = 0, col = 0; i < r && col < c; i++) {
86 //debug_print();
87 maxrow = i;
88 // 找到i到r-1行中col元素最大的那個值
89 for(j = i+1; j < r; j++) {
90 if( abs(d[j][col]) > abs(d[maxrow][col]) ){
91 maxrow = j;
92 }
93 }
94 // 最大的行和第i行交換
95 if(maxrow != i) {
96 swap_row(i, maxrow);
97 }
98 if( d[i][col] == 0 ) {
99 // 最大的那一行的當(dāng)前col值 等于0,繼續(xù)找下一列
100 col ++;
101 i--;
102 continue;
103 }
104
105 for(j = i+1; j < r; j++) {
106 if( d[j][col] ) {
107 // 當(dāng)前行的第col列如果不為0,則進行消元
108 // 以期第i行以下的第col列的所有元素都消為0
109 LL lastcoff = d[i][col];
110 LL nowcoff = d[j][col];
111 for(k = col; k <= c; k++) {
112 d[j][k] = (d[j][k] * lastcoff - d[i][k] * nowcoff) % mod;
113 if (d[j][k] < 0) d[j][k] += mod;
114 }
115 }
116 }
117 col ++;
118 }
119 // i表示從i往后的行的矩陣元素都為0
120 // 存在 (0 0 0 0 0 0 d[j][c]) (d[j][c] != 0) 的情況,方程無解
121 for(j = i; j < r; j++) {
122 if( d[j][c] ) {
123 return -1;
124 }
125 }
126 // 自由變元數(shù) 為 (變量數(shù) - 非零行的數(shù)目)
127 int free_num = c - i;
128
129 // 交換列,保證最后的矩陣為嚴(yán)格上三角,并且上三角以下的行都為0
130 for(i = 0; i < r && i < c; i++) {
131 if( !d[i][i] ) {
132 // 對角線為0
133 for(j = i+1; j < c; j++) {
134 // 在該行向后找第一個不為0的元素所在的列,交換i和這一列
135 if(d[i][j]) break;
136 }
137 if(j < c) {
138 swap_col(i, j);
139 }
140 }
141 }
142 xcnt = ( ((LL)1) << (LL)free_num );
143
144 getAns(mod);
145 return xcnt;
146 }
147
148 void debug_print() {
149 int i, j;
150 printf("-------------------------------\n");
151 for(i = 0; i < r; i++) {
152 for(j = 0; j <= c; j++) {
153 printf("%d ", d[i][j]);
154 }
155 puts("");
156 }
157 printf("-------------------------------\n");
158 }
159 };
160
來看幾道經(jīng)典的高斯消元,熟悉各種類型的高斯消元。
HDU 3359 Kind of a Blur
題意:H * W (W,H <= 10) 的矩陣A的某個元素A[i][j],從它出發(fā)到其他點的曼哈頓距離小于等于D的所有值的和S[i][j]除上可達點的數(shù)目,構(gòu)成了矩陣B。給定矩陣B,求矩陣A。
題解:將所有矩陣A的元素看成自變量,一共有H*W個變量,每個矩陣B的元素是由這些變量組合而成的,對于固定的B[i][j],曼哈頓距離在D以內(nèi)的A[x][y]的系數(shù)為1,其它為0,這樣就變成了求H*W個變量和H*W個方程的線性方程組,高斯消元求解。這題數(shù)據(jù)量比較小,所以直接采用浮點數(shù)的高斯消元即可,需要注意的是,浮點數(shù)消元的時候為了避免精度誤差,每次找最大的行,乘上一個小于1的系數(shù)進行消元,這樣可以把誤差降到最小。
PKU 1830 開關(guān)問題
題意:給定N(N < 29)個開關(guān),每個開關(guān)打開和關(guān)閉的時候會引起另外一個開關(guān)的變化,本來為打開的會變成關(guān)閉,本來關(guān)閉的會變成打開。給定N個開關(guān)的初始狀態(tài)和終止?fàn)顟B(tài),以及關(guān)聯(lián)的開關(guān)關(guān)系,求共有多少種方案從初始狀態(tài)變成終止?fàn)顟B(tài)(不計順序,并且每個開關(guān)只能操作至多一次)。
題解:由于開關(guān)只有打開和關(guān)閉兩種狀態(tài),所以對于每個開關(guān)的打開和關(guān)閉,組合一下總共有2^N種情況,枚舉所有情況判可行性,對于這個數(shù)據(jù)量來說是不現(xiàn)實的,需要想辦法優(yōu)化。
我們用X[i]來表示第i個開關(guān)的操作狀態(tài)(1表示操作,0表示不操作)。
第i個開關(guān)會被哪些開關(guān)影響是可以知道的(這個關(guān)系在輸入的時候會給出),假設(shè)影響第i個開關(guān)的開關(guān)列表為L[i][0], L[i][1], L[i][2]... 第i個開關(guān)的起始狀態(tài)為S[i],終止?fàn)顟B(tài)為E[i],則可以列出N個方程:
( X[0] * A[i][0] + X[1] * A[i][1] + ... + X[n-1] * A[i][n-1] ) % 2 = (E[i] - S[i]);
每個方程代表一個開關(guān)被它本身以及它的關(guān)聯(lián)開關(guān)操作后的最終狀態(tài),系數(shù)矩陣A[i][j]代表了開關(guān)之間的連帶關(guān)系:
1) 如果第j個開關(guān)的操作能夠影響第i個開關(guān)的狀態(tài),那么A[i][j] = 1;
2) 如果第j個開關(guān)的操作不影響第i個開關(guān)的狀態(tài),那么A[i][j] = 0;
3) 特殊的A[i][i] = 1(開關(guān)本身的操作必然會影響自己的當(dāng)前狀態(tài));
X[i]取值為0或1,這樣就是N個N元一次方程組,利用高斯消元求解即可。將增廣矩陣化簡為上三角的形式后,剩余全為0的行的個數(shù)為自由變元的個數(shù)F(自由變元就是它在取值范圍內(nèi)可以取任意值,這題是個方陣,所以自由變元的個數(shù)等于全為0的行的個數(shù)),所以,由于開關(guān)一共兩種狀態(tài),取值為0和1,所以總的解的個數(shù)為2^F。特殊的,如果某一行系數(shù)全為零,而增廣矩陣最后一列對應(yīng)行的值不為0,則表示無解。
HDU 3364 Lanterns
PKU 1830的簡單變種。那題是用開關(guān)來控制開關(guān),這題是用開關(guān)來控制燈,而且開關(guān)和燈的數(shù)目是不一樣的,這樣就導(dǎo)致了高斯矩陣并不是一個方陣,而是一個N*M的矩陣,
同樣的構(gòu)造系數(shù)矩陣的方法,當(dāng)N和M不相等的情況下,自由變元的個數(shù)就不是剩余全為0的行的個數(shù)了。其實對于一般的方程,自由變元的個數(shù)為 Free =(變量數(shù)var - 非0系數(shù)向量的個數(shù))。這題數(shù)據(jù)量比那題大,最大情況有可能是2^N,所以需要用__int64。
PKU 2065 SETI
題意:
(a1 * 10 + a2 * 11 + ... an * 1n) % P = C1
(a1 * 20 + a2 * 21 + ... an * 2n) % P = C2
(a1 * 30 + a2 * 31 + ... an * 3n) % P = C3
....
(a1 * n0 + a2 * n1 + ... an * nn) % P = Cn
給定n個以上的方程組,求滿足條件的 ai (1 <= i <= n)。
題解:如果沒有模 P,那么這個就是N個N元一次方程組,利用高斯消元可以求解,加上模P剩余后,其實原理一樣,只不過在初等行變換后,每次進行消元的時候?qū)⑺兄的,最后求解回帶的時候利用擴展歐幾里得來對每一個ai求一個最小的可行解。
例如,最后化簡的行階梯陣如下圖:
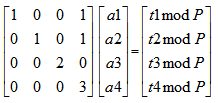
那么從后往前進行迭代求解的時候,必然會遇到兩個數(shù)相乘模P等于一個常數(shù)的情況,比如求a4的時候,有同余數(shù)方程 3*a4 % P = t4,可以表示成3*a4 + K*P = t4,其中P必然和3互素(題中有說明),所以這個方程必然有解,利用擴展歐幾里得可以求得一個最小的非負(fù)整數(shù)a4,a4求出后同理求出a3、a2、a1即可。
PKU 3185 The Water Bowls
題意:20個開關(guān)排成一排,兩邊的開關(guān)的開啟和關(guān)閉狀態(tài)會帶動相鄰的一個開關(guān),中間的開關(guān)的開啟和關(guān)閉會帶動相鄰的兩個開關(guān),問給定一個狀態(tài)能否將這些開關(guān)的狀態(tài)都變?yōu)榇蜷_狀態(tài),如果能輸出最小的操作次數(shù)。
題解:PKU 1830的變種,求最小的操作次數(shù)就是求所有解集中解的總和最小的解集,所以在進行初等行變換之后,利用dfs來枚舉所有的解,當(dāng)然如果不是自由變元的,解是確定的,由于開關(guān)開兩次和不操作是一樣的,所以每個開關(guān)的解集為{0, 1},枚舉過程中記錄當(dāng)前操作的次數(shù),如果比之前記錄的最小操作次數(shù)大,那么無須往下枚舉,直接返回,作為剪枝。由于狀態(tài)最多220種,加上適當(dāng)?shù)募糁Γ梢院芸彀呀馑殉鰜怼?/span>
HDU 3571 N-dimensional Sphere
題意:在一個N維空間中,給定一個N+1個點,求一個點使得它到所有點的距離都為R(R不給出),保證解為整數(shù),并且解的范圍為 [-1017, 1017]。
題解:對于N個未知數(shù),N+1個方程,相鄰兩個方程相減可以把二次項全部約去,剩下一次項系數(shù),則問題轉(zhuǎn)化為N個未知數(shù),N個方程的一次方程組,可以利用高斯消元求解,但是這題的數(shù)據(jù)量比較大,最大的可能解為1017,如果利用大數(shù),乘法的復(fù)雜度很高,可以采用同余的方法,所以所有加法、減法、乘法需要模一個大的素數(shù)(需要大于1017的素數(shù),可以利用拉賓米勒算法隨機生成一個大素數(shù)P),然后利用同余方程求一個最小的非負(fù)數(shù)解,在進行相乘運算的時候最大情況會超過int64,所以處理乘法運算的時候需要用到二分加法,所有的乘模運算需要化簡成加法和減法運算。利用PKU 2065 的求法可以求得所有可行解,由于這題的數(shù)據(jù)量可能為負(fù)數(shù),同余的情況下求出來的是非負(fù)數(shù),為了消除這種情況,對所有輸入的值加上一個偏移量1017,最后的解再減去這個偏移量,注意最后的答案減去偏移量的時候不需要取模(否則就沒有意義了)。
PKU 1288 Sly Number
題意:定義Sly Number為只有{0, 1, 2}三種數(shù)字的一維數(shù)組,對于兩個Sly Number:A 和B的乘法操作如下:

圖1
相乘后的取余操作如下:
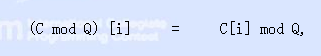
圖2
定義ONE為A[0] = 1, A[i] = 0 (i = 1, 2, ...N-1),給定A和Q,求A對于Q的逆元,即(A * B) mod Q = ONE中的B。
題解:首先B也是Sly Number,結(jié)合圖中的等式,可以列出N個方程:
C[0] = (A[0]*B[0]) + ( A[1]*B[N-1] + A[2]*B[N-2] + ... + A[N-1]*B[1]) ;
C[1] = (A[0]*B[1] + A[1]*B[0]) + ( A[2]*B[N-1] + ... + A[N-1]*B[2] );
...
C[N-1] = (A[0]*B[N-1] + A[1]*B[N-2] +... A[N-1]*B[0]);
由模的定義,可知C[0] mod Q = 1, C[i] mod Q = 0 (i = 1, 2, ... N-1)
于是可以列出N個方程N個未知數(shù)的模線性方程組,利用圖1的下標(biāo)關(guān)系,將A[i]填入對應(yīng)的系數(shù)矩陣中,用高斯消元化解增廣矩陣為上三角梯陣,然后從N-1到0枚舉B[i] 的取值(取值為0、1、2),當(dāng)B[i](0 < i < N)滿足條件則遞歸枚舉B[i-1],知道所有的B[i]枚舉完畢,則表明至少有一個解,否則無解。
SGU 173 Coins
題意:N(2 <= N <= 50)個硬幣排成一排,有的人頭朝上(用0表示),有的則是字朝上(用1表示),對這一排硬幣進行M(1 <= M <= 10)次X變換之后的狀態(tài)已知,求初始的硬幣狀態(tài)。
定義一次X變換如下:
1、從這一排硬幣的Si(1 <= Si <= N, 1<= i <= M)位置取連續(xù)的K(2 <= K <= N)個硬幣;
2、對這取出來的K個硬幣進行一次循環(huán)左移操作;
3、掃描前K-1個硬幣,如果第i個硬幣字朝上(即為1),并且Ai等于1,那么將第K個硬幣進行一次翻轉(zhuǎn);
4、重復(fù)2) - 3) 操作Di(Di <= 106)次;
上述X變換的3)中出現(xiàn)了Ai,但是題目并未給出Ai ( 1 <= i <= K-1),而是給出了L(L <= 200)個X變換之前的狀態(tài)和之后的狀態(tài)(每個狀態(tài)為K個硬幣),需要利用這L條關(guān)系來求出Ai,并且題目保證Ai有且僅有一個解。
題解:題目兜兜轉(zhuǎn)轉(zhuǎn)繞了一大圈,實在很難讀懂,只能通過樣例來琢磨意思。這個題目分為兩部分,首先是要把Ai求出來,然后再根據(jù)Ai的值和結(jié)束狀態(tài)反推初始狀態(tài)。
首先來看樣例,L = 2, K = 3 兩組X變換的前后狀態(tài)為010 -> 101、101 -> 011。
對于第一對狀態(tài),010循環(huán)左移后為100,第K個硬幣和結(jié)束狀態(tài)不相符,說明前2(即K - 1)個硬幣中字朝上的硬幣對應(yīng)的Ai必定有奇數(shù)個為1(這樣才能使第K個硬幣從0翻轉(zhuǎn)到1),而前二個硬幣只有第一個為1,所以A1 = 1;同理對于第二個狀態(tài),可以求出A2 = 0;
模擬一下樣例可以大致了解題目的用意,但是對于一般的情況還是需要用系統(tǒng)的方法去分析,讓我們來看下一般的情況,對于某一對狀態(tài)如下:
初始狀態(tài)S = S1S2S3...SK-1SK 結(jié)束狀態(tài)T = T1T2T3...TK-1TK
將初始狀態(tài)循環(huán)左移一次后為S’ = S2S3...SK-1SKS1,由于循環(huán)左移之后前K-1個硬幣的狀態(tài)不會再發(fā)生改變,所以有 S2S3...SK-1SK == T1T2T3...TK-1,當(dāng)然這一點,題目數(shù)據(jù)是會保證的,我們不需要關(guān)心,我們需要關(guān)心的就是S1和TK 是否相等,如果S1和TK 相等,那么前T1T2T3...TK-1 中為1的對應(yīng)的Ai=1的個數(shù)為偶數(shù)個,否則為奇數(shù)個。利用更加通俗的解釋,即(T1 A1 + T2 A2 + T3A3 + ...+ TK-1AK-1) mod 2 = S1 ^ TK,這個方程中,只有Ai是未知數(shù),那么對于L個條件,我們可以列出L條方程,這樣就轉(zhuǎn)變成了L個方程K-1個未知數(shù)的模線性方程組,可以利用高斯消元求解Ai。
Ai求出來后,給定一個結(jié)束狀態(tài),模擬M*Di次逆向操作,每次操作需要進行字符串的右移(因為是逆向,所以要和題目的左移相反)操作,每次右移最多牽涉N次原子操作,所以總的復(fù)雜度為O(N*M*Di),復(fù)雜度過大,但是注意到這里的N <= 50,所以我們可以將每個狀態(tài)壓縮到一個int64的整數(shù)中,A1A2A3..AK-1也可以壓縮成一個int64的整數(shù),右移操作可以通過位運算在O(1)的時間內(nèi)解決。其中有一步會涉及到判斷一個數(shù)的二進制表示中有多少個1的問題,網(wǎng)上各種面試題很多,不再累述,比較方便、效率也還可以的是采用樹狀數(shù)組中lowbit的思想,即利用 x 減去 (x&(-x)) (其中 x&(-x) = 2^k, k為x二進制末尾0的個數(shù)),逐個將1消去,直到x = 0為止,迭代消去的次數(shù)就是1的個數(shù)。
posted on 2014-06-08 19:55 英雄哪里出來 閱讀(8797) 評論(2) 編輯 收藏 引用 所屬分類: 算法專輯


