pku 2154 Color
burnside是一種計數方法,用來計算含有不等價類的數量, 簡單說就是對于每個置換 fi ,他都對一定量的著色無效(該著色經過fi置換不變),設這些著色數量為ai, 所有ai的平均數就是不等價類的數量, 當然也可以變換求和順序, 先考慮每中著色, 再求他的穩定核, 但一般情況是置換數很少, 著色數很多, 所以前者很常用
這道題是比較經典的循環排列計數,有 N 個置換{ P^0 = r, P^1, P^2, P^(n-1)} r為單位置換
寫個小程序觀察 ,發現 P^x 的循環結恰好是gcd(x , N)
這樣我們就有一個較好的求和式子 :
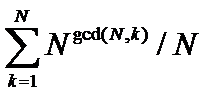
但N可到10^9,這個求和式直接用不現實,繼續觀察,發現這些數都是N的約數,自然會想改變求和順序,先考慮每個約數,我又寫了個小程序輸出每個約數的數量(一開始就知道他大概跟歐拉數有關系,但沒有發現明顯的積性),打出表來一看,原來因子x的數量是Phi(N/x);這樣式子就變成了
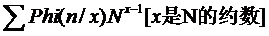 φ(N/pi)就是 1 -- N 中所有滿足gcd(i,N)=pi 的 i 的個數
φ(N/pi)就是 1 -- N 中所有滿足gcd(i,N)=pi 的 i 的個數
(Hint gcd(i,N)=pi 等價于 gcd(i/pi,N/pi)=1 ) 要約數盡量的多,就要不同的素因子盡量多,N最多不會有10個不同的素因子,約數不會超過1024個,而且約數越多,約數就會變小,求約數的歐拉數雖然是O( sqrt(N) )的,但需要對于其中一個約數計算超過20次的不會超過3個,有了這些估計,雖然具體的算法復雜度不知道, 我決定冒險試試,應該不會超時。結果跑了600ms,還是比較理想的
posted on 2009-04-03 15:58
wangzhihao 閱讀(2166)
評論(0) 編輯 收藏 引用 所屬分類:
math