PKU
1066 是一道感覺很好的題,用同側異側(位置)來表示的話思路會很清晰。
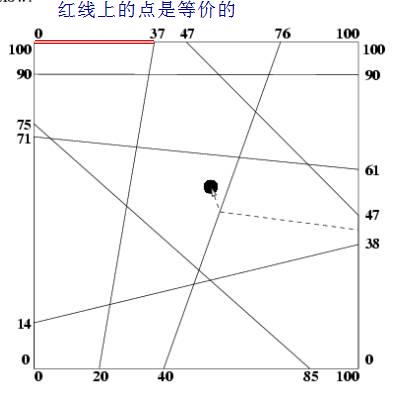
首先要從起點到終點穿過一道墻,等價于起點和終點在墻的異側,這樣就清楚的表示了穿過一道墻的充要條件。
接下來也變得簡單,就是枚舉終點,終點顯然在正方形的邊上。很快能發現他們是一塊一塊的。緊鄰的交點(墻和正方形所交的點)所構成的線段上的點相對墻的位置是同側。因為他們沒有被任何墻分割開。也就不可能異側。
這樣只要分塊枚舉,一塊枚舉只需一個點。
1 #include<iostream>
2 #include<cmath>
3 #include<algorithm>
4 using namespace std;
5 double const EPS = 1e-8;
6 const int INF = 1<<30;
7
8 int dcmp(double x){return x < -EPS ? -1 : x > EPS;}
9
10 struct Point{
11 double x,y;
12 Point(){}
13 Point(double a, double b):x(a), y(b){}
14 bool operator<(Point a){return atan2(y - 50, x - 50) < atan2(a.y - 50, a.x - 50); }
15 };
16
17 struct Line{Point a, b;};
18
19 Point P[128], s, t;
20 Line L[36];
21 int n, cnt, best;
22
23 double xmult(Point p1, Point p2 , Point p0)
24 {
25 return (p1.x - p0.x)*(p2.y - p0.y)-(p2.x - p0.x)*(p1.y - p0.y);
26 }
27 bool same_side(Point p1, Point p2, Line L)
28 {
29 return dcmp(xmult(L.b, p1, L.a) * xmult(L.b, p2, L.a)) >= 0;
30 }
31
32 int main()
33 {
34 int i, j, ans;
35 best = INF; cnt = 0;
36 P[cnt++] = Point(0, 0);
37 P[cnt++] = Point(100, 0);
38 P[cnt++] = Point(0, 100);
39 P[cnt++] = Point(100, 100);
40
41 cin >> n;
42 for(i = 0; i < n; i++)
43 {
44 cin>> L[i].a.x >> L[i].a.y >> L[i].b.x >> L[i].b.y;
45 P[cnt++] = L[i].a;
46 P[cnt++] = L[i].b;
47 }
48 cin>> s.x >> s.y;
49
50 sort(P, P+cnt);
51
52 for(i = 0; i < cnt; i++ )
53 {
54 ans = 0;
55 t = Point( (P[i].x + P[(i+1)%cnt].x)/2, (P[i].y + P[(i+1)%cnt].y)/2 );
56 for(j = 0; j < n; j++)
57 if(!same_side(s, t, L[j]))ans++;
58 if(ans < best) best = ans;
59 }
60
61 printf("Number of doors = %d\n", best+1);
62 }
posted on 2009-07-24 16:20
wangzhihao 閱讀(627)
評論(5) 編輯 收藏 引用 所屬分類:
geometry