這可能是最有趣的一節(jié)。排序的考題，在各大公司的筆試?yán)镒钕矚g出了，但我看多數(shù)考得都很簡(jiǎn)單，通常懂得冒泡排序就差不多了，確實(shí)，我在剛學(xué)數(shù)據(jù)機(jī)構(gòu)時(shí)候，覺(jué)得冒泡排序真的很“精妙”，我怎么就想不出呢？呵呵，其實(shí)冒泡通常是效率最差的排序算法，差多少？請(qǐng)看本文，你一定不會(huì)后悔的。

1、冒泡排序（Bubbler Sort）

前面剛說(shuō)了冒泡排序的壞話，但冒泡排序也有其優(yōu)點(diǎn)，那就是好理解，穩(wěn)定，再就是空間復(fù)雜度低，不需要額外開(kāi)辟數(shù)組元素的臨時(shí)保存控件，當(dāng)然了，編寫起來(lái)也容易。

其算法很簡(jiǎn)單，就是比較數(shù)組相鄰的兩個(gè)值，把大的像泡泡一樣“冒”到數(shù)組后面去，一共要執(zhí)行N的平方除以2這么多次的比較和交換的操作（N為數(shù)組元素），其復(fù)雜度為Ο(n²)，如圖：

 2、直接插入排序（Straight Insertion Sort）

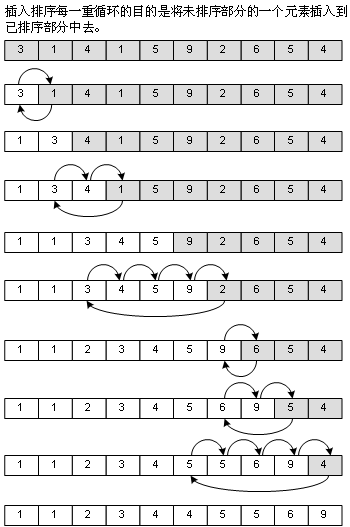
冒泡法對(duì)于已經(jīng)排好序的部分（上圖中，數(shù)組顯示為白色底色的部分）是不再訪問(wèn)的，插入排序卻要，因?yàn)樗姆椒ň褪菑奈磁判虻牟糠种腥〕鲆粋€(gè)元素，插入到已經(jīng)排好序的部分去，插入的位置我是從后往前找的，這樣可以使得如果數(shù)組本身是有序（順序）的話，速度會(huì)非常之快，不過(guò)反過(guò)來(lái)，數(shù)組本身是逆序的話，速度也就非常之慢了，如圖：

3、二分插入排序（Binary Insertion Sort）

這是對(duì)直接插入排序的改進(jìn)，由于已排好序的部分是有序的，所以我們就能使用二分查找法確定我們的插入位置，而不是一個(gè)個(gè)找，除了這點(diǎn)，它跟插入排序沒(méi)什么區(qū)別，至于二分查找法見(jiàn)我前面的文章（本系列文章的第四篇）。圖跟上圖沒(méi)什么差別，差別在于插入位置的確定而已，性能卻能因此得到不少改善。（性能分析后面會(huì)提到）

4、直接選擇排序（Straight Selection Sort）

這是我在學(xué)數(shù)據(jù)結(jié)構(gòu)前，自己能夠想得出來(lái)的排序法，思路很簡(jiǎn)單，用打擂臺(tái)的方式，找出最大的一個(gè)元素，和末尾的元素交換，然后再?gòu)念^開(kāi)始，查找第1個(gè)到第N-1個(gè)元素中最大的一個(gè)，和第N-1個(gè)元素交換……其實(shí)差不多就是冒泡法的思想，但整個(gè)過(guò)程中需要移動(dòng)的元素比冒泡法要少，因此性能是比冒泡法優(yōu)秀的。看圖：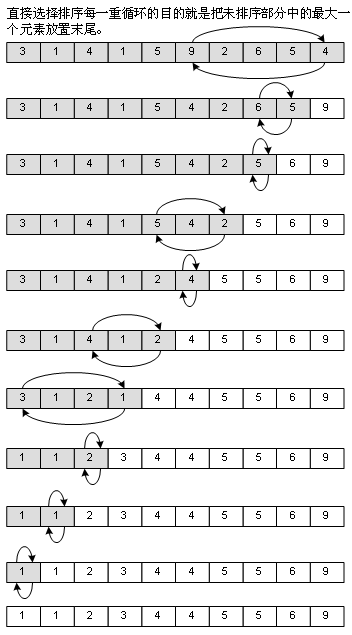

5、快速排序（Quick Sort）

快速排序是非常優(yōu)秀的排序算法，初學(xué)者可能覺(jué)得有點(diǎn)難理解，其實(shí)它是一種“分而治之”的思想，把大的拆分為小的，小的再拆分為更小的，所以你一會(huì)兒從代碼中就能很清楚地看到，用了遞歸。如圖：

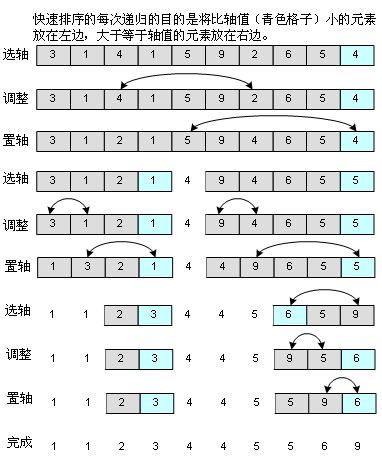
其中要選擇一個(gè)軸值，這個(gè)軸值在理想的情況下就是中軸，中軸起的作用就是讓其左邊的元素比它小，它右邊的元素不小于它。（我用了“不小于”而不是“大于”是考慮到元素?cái)?shù)值會(huì)有重復(fù)的情況，在代碼中也能看出來(lái)，如果把“>=”運(yùn)算符換成“>”，將會(huì)出問(wèn)題）當(dāng)然，如果中軸選得不好，選了個(gè)最大元素或者最小元素，那情況就比較糟糕，我選軸值的辦法是取出第一個(gè)元素，中間的元素和最后一個(gè)元素，然后從這三個(gè)元素中選中間值，這已經(jīng)可以應(yīng)付絕大多數(shù)情況。

6、改進(jìn)型快速排序（Improved Quick Sort）

快速排序的缺點(diǎn)是使用了遞歸，如果數(shù)據(jù)量很大，大量的遞歸調(diào)用會(huì)不會(huì)導(dǎo)致性能下降呢？我想應(yīng)該會(huì)的，所以我打算作這么種優(yōu)化，考慮到數(shù)據(jù)量很小的情況下，直接選擇排序和快速排序的性能相差無(wú)幾，那當(dāng)遞歸到子數(shù)組元素?cái)?shù)目小于30的時(shí)候，我就是用直接選擇排序，這樣會(huì)不會(huì)提高一點(diǎn)性能呢？我后面分析。排序過(guò)程可以參考前面兩個(gè)圖，我就不另外畫了。

7、桶排序（Bucket Sort）

這是迄今為止最快的一種排序法，其時(shí)間復(fù)雜度僅為Ο(n)，也就是線性復(fù)雜度！不可思議吧？但它是有條件的。舉個(gè)例子：一年的全國(guó)高考考生人數(shù)為500萬(wàn)，分?jǐn)?shù)使用標(biāo)準(zhǔn)分，最低100，最高900，沒(méi)有小數(shù)，你把這500萬(wàn)元素的數(shù)組排個(gè)序。我們抓住了這么個(gè)非常特殊的條件，就能在毫秒級(jí)內(nèi)完成這500萬(wàn)的排序，那就是：最低100，最高900，沒(méi)有小數(shù)，那一共可出現(xiàn)的分?jǐn)?shù)可能有多少種呢？一共有900-100+1=801，那么多種，想想看，有沒(méi)有什么“投機(jī)取巧”的辦法？方法就是創(chuàng)建801個(gè)“桶”，從頭到尾遍歷一次數(shù)組，對(duì)不同的分?jǐn)?shù)給不同的“桶”加料，比如有個(gè)考生考了500分，那么就給500分的那個(gè)桶（下標(biāo)為500-100）加1，完成后遍歷一下這個(gè)桶數(shù)組，按照桶值，填充原數(shù)組，100分的有1000人，于是從0填到999，都填1000，101分的有1200人，于是從1000到2019，都填入101……如圖：

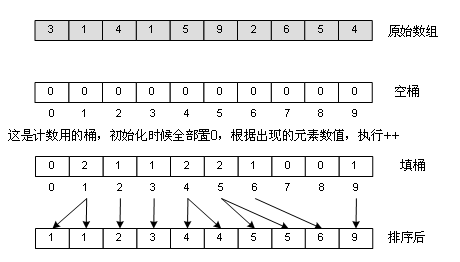
很顯然，如果分?jǐn)?shù)不是從100到900的整數(shù)，而是從0到2億，那就要分配2億個(gè)桶了，這是不可能的，所以桶排序有其局限性，適合元素值集合并不大的情況。

8、基數(shù)排序（Radix Sort）

基數(shù)排序是對(duì)桶排序的一種改進(jìn)，這種改進(jìn)是讓“桶排序”適合于更大的元素值集合的情況，而不是提高性能。它的思想是這樣的，比如數(shù)值的集合是8位整數(shù)，我們很難創(chuàng)建一億個(gè)桶，于是我們先對(duì)這些數(shù)的個(gè)位進(jìn)行類似桶排序的排序（下文且稱作“類桶排序”吧），然后再對(duì)這些數(shù)的十位進(jìn)行類桶排序，再就是百位……一共做8次，當(dāng)然，我說(shuō)的是思路，實(shí)際上我們通常并不這么干，因?yàn)?span>C++的位移運(yùn)算速度是比較快，所以我們通常以“字節(jié)”為單位進(jìn)行桶排序。但下圖為了畫圖方便，我是以半字節(jié)（4 bit）為單位進(jìn)行類桶排序的，因?yàn)樽止?jié)為單位進(jìn)行桶排得畫256個(gè)桶，有點(diǎn)難畫，如圖：

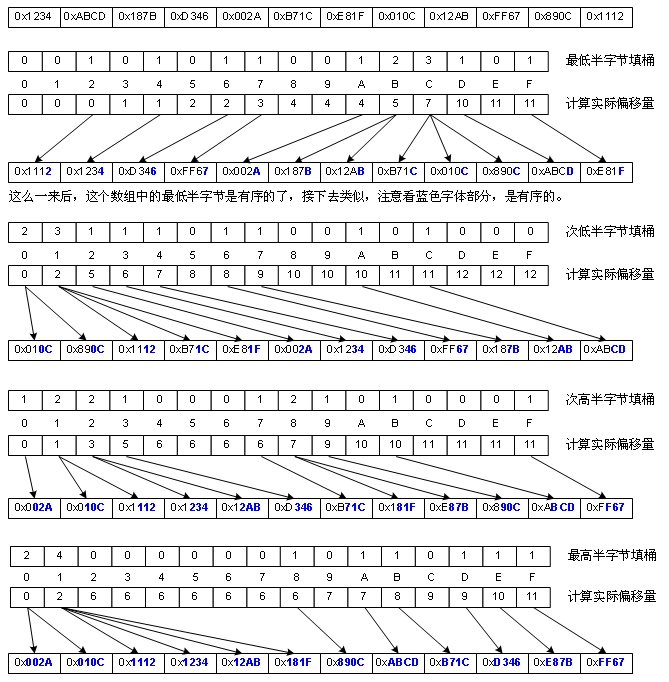
基數(shù)排序適合數(shù)值分布較廣的情況，但由于需要額外分配一個(gè)跟原始數(shù)組一樣大的暫存空間，它的處理也是有局限性的，對(duì)于元素?cái)?shù)量巨大的原始數(shù)組而言，空間開(kāi)銷較大。性能上由于要多次“類桶排序”，所以不如桶排序。但它的復(fù)雜度跟桶排序一樣，也是Ο(n)，雖然它用了多次循環(huán)，但卻沒(méi)有循環(huán)嵌套。

9、性能分析和總結(jié)

先不分析復(fù)雜度為Ο(n)的算法，因?yàn)樗俣忍欤矣行l件限制，我們先分析前六種算法，即：冒泡，直接插入，二分插入，直接選擇，快速排序和改進(jìn)型快速排序。

我的分析過(guò)程并不復(fù)雜，嘗試產(chǎn)生一個(gè)隨機(jī)數(shù)數(shù)組，數(shù)值范圍是0到7FFF，這正好可以用C++的隨機(jī)函數(shù)rand()產(chǎn)生隨機(jī)數(shù)來(lái)填充數(shù)組，然后嘗試不同長(zhǎng)度的數(shù)組，同一種長(zhǎng)度的數(shù)組嘗試10次，以此得出平均值，避免過(guò)多波動(dòng)，最后用Excel對(duì)結(jié)果進(jìn)行分析，OK，上圖了。

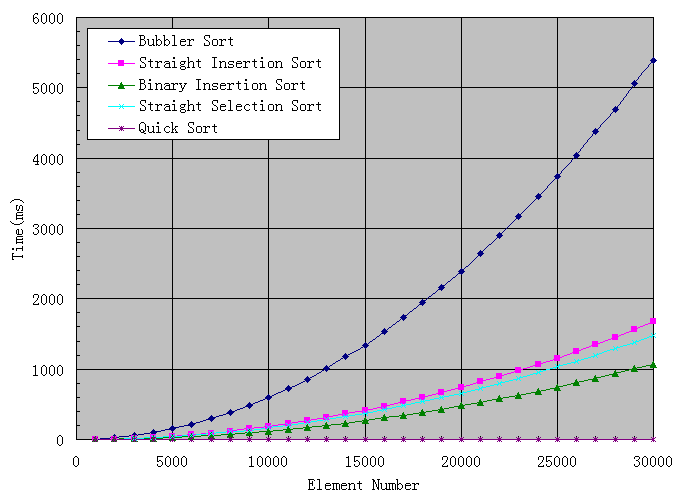
最差的一眼就看出來(lái)了，是冒泡，直接插入和直接選擇旗鼓相當(dāng)，但我更偏向于使用直接選擇，因?yàn)樗悸泛?jiǎn)單，需要移動(dòng)的元素相對(duì)較少，況且速度還稍微快一點(diǎn)呢，從圖中看，二分插入的速度比直接插入有了較大的提升，但代碼稍微長(zhǎng)了一點(diǎn)點(diǎn)。

令人感到比較意外的是快速排序，3萬(wàn)點(diǎn)以內(nèi)的快速排序所消耗的時(shí)間幾乎可以忽略不計(jì)，速度之快，令人振奮，而改進(jìn)型快速排序的線跟快速排序重合，因此不畫出來(lái)。看來(lái)要對(duì)快速排序進(jìn)行單獨(dú)分析，我加大了數(shù)組元素的數(shù)目，從5萬(wàn)到150萬(wàn)，畫出下圖：

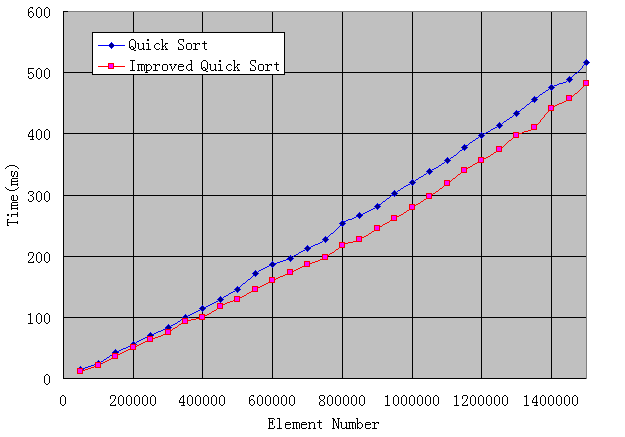
可以看到，即便到了150萬(wàn)點(diǎn)，兩種快速排序也僅需差不多半秒鐘就完成了，實(shí)在快，改進(jìn)型快速排序性能確實(shí)有微略提高，但并不明顯，從圖中也能看出來(lái)，是不是我設(shè)置的最小快速排序元素?cái)?shù)目不太合適？但我嘗試了好幾個(gè)值都相差無(wú)幾。

最后看線性復(fù)雜度的排序，速度非常驚人，我從40萬(wàn)測(cè)試到1200萬(wàn)，結(jié)果如圖：

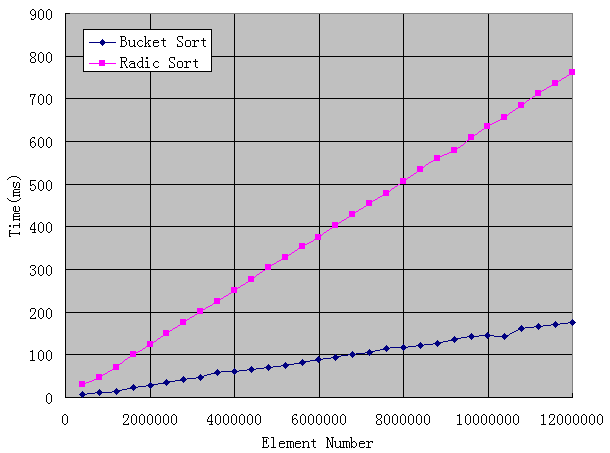
可見(jiàn)稍微調(diào)整下算法，速度可以得到質(zhì)的飛升，而不是我們以前所認(rèn)為的那樣：再快也不會(huì)比冒泡法快多少啊？

我最后制作一張表，比較一下這些排序法：

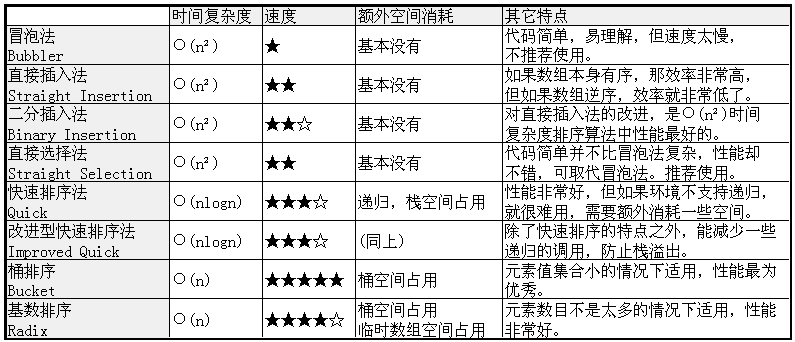
還有一個(gè)最后：附上我的代碼。